13.4课程学习 最短路径问题 课件(共30张PPT)
文档属性
| 名称 | 13.4课程学习 最短路径问题 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 17:02:22 | ||
图片预览




文档简介
(共30张PPT)
13.4课程学习 最短路径问题
人教版 八年级上册
教学目标
【教学目标】
1.知识与技能
能利用轴对称解决简单的最短路径问题
2.过程与方法
通过观察、操作、交流等活动增强动手解决问题能力。
3.情感态度和价值观
体会图形的变化在解决最值问题中的作用,感悟转化思想。
【重点】利用轴对称将最短路径问题转化为“两点之间、线段最短”问题。
【难点】探索发现“最短路径”的方案,确定最短路径的作图及说理。
回顾复习
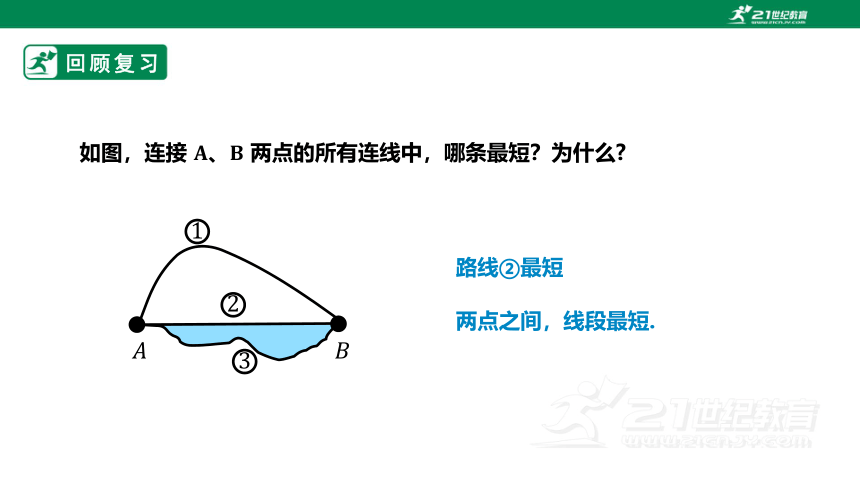
如图,连接 、 两点的所有连线中,哪条最短?为什么
2
1
3
路线②最短
两点之间,线段最短.
回顾复习
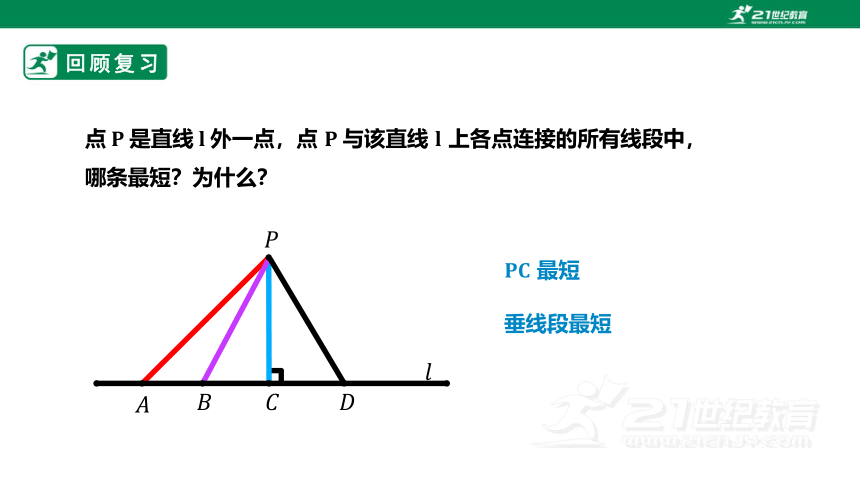
点是直线外一点,点 与该直线 上各点连接的所有线段中,哪条最短?为什么?
最短
1
1
1
1
1
1
1
垂线段最短
新知探究
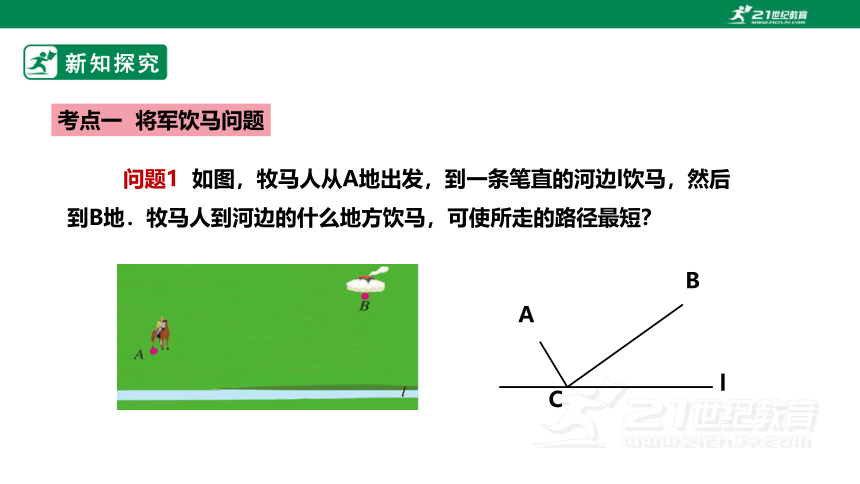
问题1 如图,牧马人从A地出发,到一条笔直的河边l饮马,然后到B地.牧马人到河边的什么地方饮马,可使所走的路径最短?
B
A
l
C
考点一 将军饮马问题
新知探究
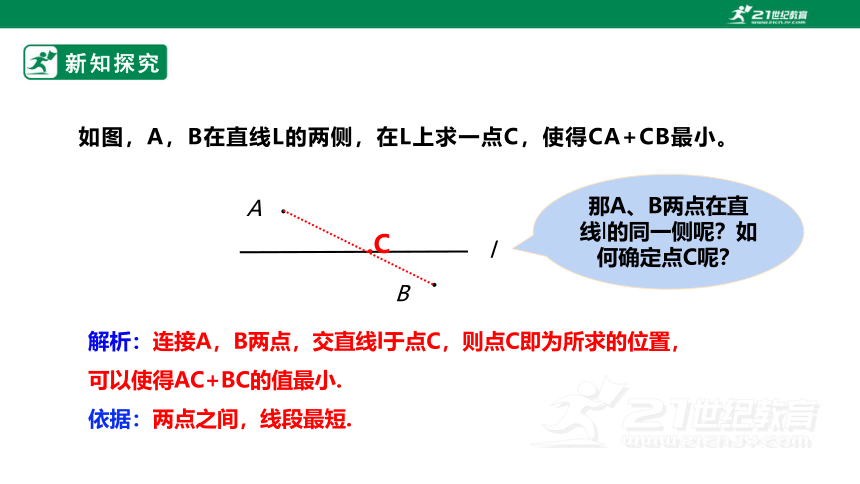
如图,A,B在直线L的两侧,在L上求一点C,使得CA+CB最小。
A
B
l
解析:连接A,B两点,交直线l于点C,则点C即为所求的位置,可以使得AC+BC的值最小.
依据:两点之间,线段最短.
.C
那A、B两点在直线l的同一侧呢?如何确定点C呢?
新知探究
A
B
l
你能利用两点分别在直线两侧的解题思路,来解决两点在直线同一侧的问题吗?
分析:如果我们能够把点B转移到直线l的另外一侧B′,同时使得对直线上任意一点C,满足BC=B′C,就可以将问题转化为“两点分别在直线两侧的情况”.那么在直线l上使得满足BC=B′C的点应该怎么找呢?
新知探究
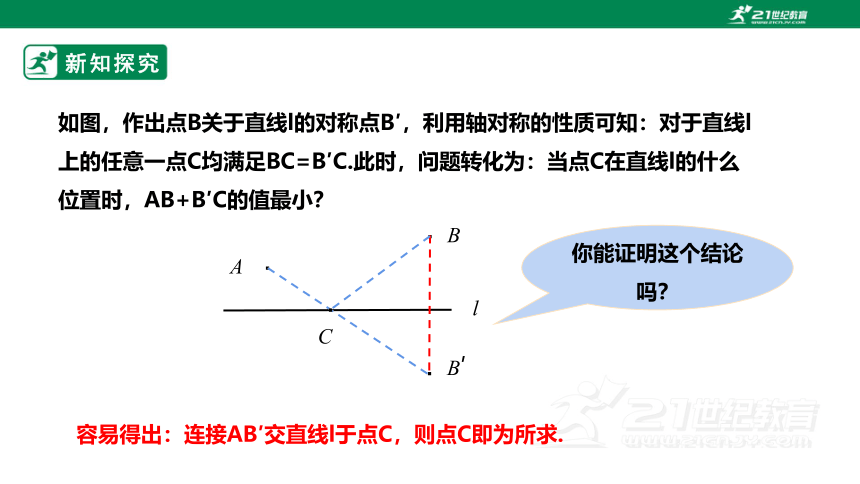
如图,作出点B关于直线l的对称点B′,利用轴对称的性质可知:对于直线l上的任意一点C均满足BC=B′C.此时,问题转化为:当点C在直线l的什么位置时,AB+B′C的值最小?
B′
容易得出:连接AB′交直线l于点C,则点C即为所求.
A
B
l
C
你能证明这个结论吗?
新知探究
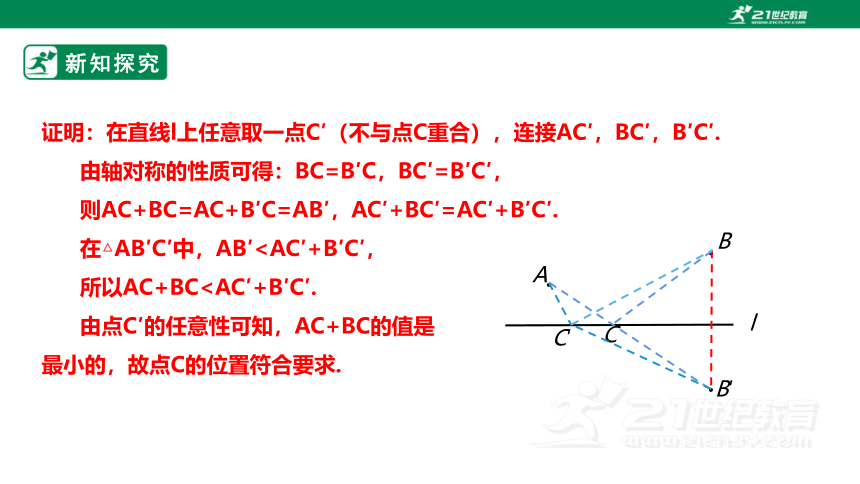
证明:在直线l上任意取一点C′(不与点C重合),连接AC′,BC′,B′C′.
由轴对称的性质可得:BC=B′C,BC′=B′C′,
则AC+BC=AC+B′C=AB′,AC′+BC′=AC′+B′C′.
在△AB′C′中,AB′所以AC+BC由点C′的任意性可知,AC+BC的值是
最小的,故点C的位置符合要求.
l
A
B
B′
C
C′
归纳总结
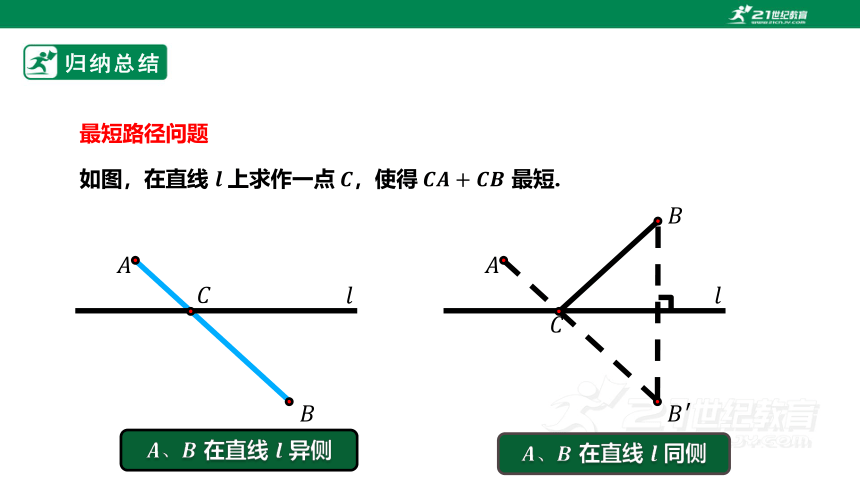
最短路径问题
如图,在直线 上求作一点,使得 最短.
在直线 异侧
在直线 同侧
归纳总结
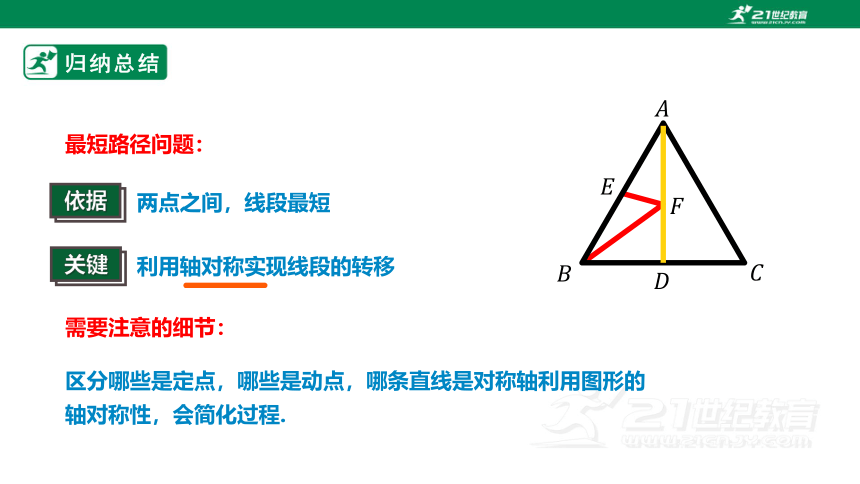
最短路径问题:
两点之间,线段最短
依据
利用轴对称实现线段的转移
关键
需要注意的细节:
区分哪些是定点,哪些是动点,哪条直线是对称轴利用图形的轴对称性,会简化过程.
针对训练
1.有两棵树位置如图,树的底部分别为 地上有一只昆虫沿着—的路径在地面上爬行. 小树顶处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶 处. 问小鸟飞至之间何处时,飞行距离最短,在图中画出该点的位置.
作法:
针对训练
2.如图,A,B两个小镇在河的同侧,现要在笔直的河边a上修建一个自来水厂分别向两个镇供水,如何选择自来水厂的位置,可使用的水管最短?
解:如图,作点B关于河边a的对称点B′,连接AB′交河边a于点P,则点P所在的位置为所求的自来水厂的位置.
A
B
a
B′
P
针对训练
3.如图,直线l是一条河,P、Q是两个村庄.欲在l上的某处修建一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需要管道最短的是( )
P
Q
l
A
M
P
Q
l
B
M
P
Q
l
C
M
P
Q
l
D
M
D
新知探究
如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,桥造在何处可以使得从A到B的路径AMNB最短?(假定河是平行的直线,桥要与河垂直)
A
B
a
b
M
N
考点二 造桥选址问题
新知探究
这是个实际问题,你能用自己理解的语言描述一下吗?
如图所示:将河的两岸看成两条平行线a和b,N为直线b上的一个动点,MN垂直于直线b,交直线a于点M.当点N在什么位置的时候,AM+MN+NB的值最小?
A
B
a
b
M
N
新知探究
A
B
M
N
a
b
(1)由于河岸宽度是固定的,因此当AM+NB最小时,AM+MN+NB最小.问题可转化为:当点N在直线b的什么位置时,AM+NB最小?
新知探究
(2)如图,将AM沿与河岸垂直的方向平移,点M移动到点N,点A移动到点A′,则AA′=MN,AM+NB=A′N+NB.
问题转化为:当点N在直线b的什么位置时,A′N+NB最小?
A
B
M
N
a
b
A′
新知探究
(3)如图,在连接A′,B两点的线中,线段A′B最短.因此,线段A′B与直线b的交点N的位置即为所求.
A
B
M
N
a
b
A′
你能证明此时AM+MN+NB最小吗?
新知探究
在直线b上另外任意取一点N′,过点N′作N′M′⊥a,垂足为M′,连接AM′,A′N′,N′B,证明AM+MN+NB<AM′+M′N′+N′B.
A
B
M
N
a
b
A′
M′
N′
新知探究
证明:在△A′N′B中,
∵A′B<A′N′+BN′,
∴A′N+BN+MN<AM′+BN′+M′N′.
∴AM+MN+BN<AM′+M′N′+BN′.
即AM+MN+BN最小.
N′
A
B
M
N
a
b
A′
M′
归纳总结
1.实际问题用数学语言表达.
2.利用平移,实现线段的转移.
3.把已知问题转化成容易解决的问题.
4.用符号语言进行推理和表达.
归纳总结
最短路径问题
造桥选址问题
练习
归纳总结
化归思想.
利用轴对称、平移等变化,把已知问题转化为容易解决的问题.
两点之间,线段最短.
依据
方法
思想
针对训练
作法:1.将点 沿直线 方向平移至 ,使得 .
3.连接 ,与直线 交于一点即为所求点 .
2.作 关于直线 的对称点 .
4.在点 左侧取点 ,使得 ,即为所求点 .
1.已知线段 ,点 在直线 的同侧,在直线 上求作两点 ,(点 在点 的左侧)且 ,使得四边形 的周长最小.
针对训练
2.如图,荆州古城河在CC′处直角转弯,河宽相同,从A处到B处,须经两座桥:DD ′,EE ′(桥宽不计),设护城河以及两座桥都是东西、南北方向的,怎样架桥可使ADD ′E ′EB的路程最短?
A
D
D ′
C
C′
E
E′
B
针对训练
解:作AF⊥CD,且AF=河宽,作BG ⊥CE,且BG=河宽,连接GF,与河岸相交于E ′,D′.作DD′,EE′即为桥.
理由:由作图法可知,AF//DD′,AF=DD′,则四边形AFD′D为平行四边形,于是AD=FD′,
同理,BE=GE′,
由两点之间线段最短可知,GF最小.
A
D ′
C
C′
E
E′
B
F
G
D
课堂总结
解决最短路径问题的方法
在解决最短路径问题时,我们通常利用轴对称、平移等变换把未知问题转化为已解决的问题,从而作出最短路径的选择.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.4课程学习 最短路径问题
人教版 八年级上册
教学目标
【教学目标】
1.知识与技能
能利用轴对称解决简单的最短路径问题
2.过程与方法
通过观察、操作、交流等活动增强动手解决问题能力。
3.情感态度和价值观
体会图形的变化在解决最值问题中的作用,感悟转化思想。
【重点】利用轴对称将最短路径问题转化为“两点之间、线段最短”问题。
【难点】探索发现“最短路径”的方案,确定最短路径的作图及说理。
回顾复习
如图,连接 、 两点的所有连线中,哪条最短?为什么
2
1
3
路线②最短
两点之间,线段最短.
回顾复习
点是直线外一点,点 与该直线 上各点连接的所有线段中,哪条最短?为什么?
最短
1
1
1
1
1
1
1
垂线段最短
新知探究
问题1 如图,牧马人从A地出发,到一条笔直的河边l饮马,然后到B地.牧马人到河边的什么地方饮马,可使所走的路径最短?
B
A
l
C
考点一 将军饮马问题
新知探究
如图,A,B在直线L的两侧,在L上求一点C,使得CA+CB最小。
A
B
l
解析:连接A,B两点,交直线l于点C,则点C即为所求的位置,可以使得AC+BC的值最小.
依据:两点之间,线段最短.
.C
那A、B两点在直线l的同一侧呢?如何确定点C呢?
新知探究
A
B
l
你能利用两点分别在直线两侧的解题思路,来解决两点在直线同一侧的问题吗?
分析:如果我们能够把点B转移到直线l的另外一侧B′,同时使得对直线上任意一点C,满足BC=B′C,就可以将问题转化为“两点分别在直线两侧的情况”.那么在直线l上使得满足BC=B′C的点应该怎么找呢?
新知探究
如图,作出点B关于直线l的对称点B′,利用轴对称的性质可知:对于直线l上的任意一点C均满足BC=B′C.此时,问题转化为:当点C在直线l的什么位置时,AB+B′C的值最小?
B′
容易得出:连接AB′交直线l于点C,则点C即为所求.
A
B
l
C
你能证明这个结论吗?
新知探究
证明:在直线l上任意取一点C′(不与点C重合),连接AC′,BC′,B′C′.
由轴对称的性质可得:BC=B′C,BC′=B′C′,
则AC+BC=AC+B′C=AB′,AC′+BC′=AC′+B′C′.
在△AB′C′中,AB′
最小的,故点C的位置符合要求.
l
A
B
B′
C
C′
归纳总结
最短路径问题
如图,在直线 上求作一点,使得 最短.
在直线 异侧
在直线 同侧
归纳总结
最短路径问题:
两点之间,线段最短
依据
利用轴对称实现线段的转移
关键
需要注意的细节:
区分哪些是定点,哪些是动点,哪条直线是对称轴利用图形的轴对称性,会简化过程.
针对训练
1.有两棵树位置如图,树的底部分别为 地上有一只昆虫沿着—的路径在地面上爬行. 小树顶处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶 处. 问小鸟飞至之间何处时,飞行距离最短,在图中画出该点的位置.
作法:
针对训练
2.如图,A,B两个小镇在河的同侧,现要在笔直的河边a上修建一个自来水厂分别向两个镇供水,如何选择自来水厂的位置,可使用的水管最短?
解:如图,作点B关于河边a的对称点B′,连接AB′交河边a于点P,则点P所在的位置为所求的自来水厂的位置.
A
B
a
B′
P
针对训练
3.如图,直线l是一条河,P、Q是两个村庄.欲在l上的某处修建一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需要管道最短的是( )
P
Q
l
A
M
P
Q
l
B
M
P
Q
l
C
M
P
Q
l
D
M
D
新知探究
如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,桥造在何处可以使得从A到B的路径AMNB最短?(假定河是平行的直线,桥要与河垂直)
A
B
a
b
M
N
考点二 造桥选址问题
新知探究
这是个实际问题,你能用自己理解的语言描述一下吗?
如图所示:将河的两岸看成两条平行线a和b,N为直线b上的一个动点,MN垂直于直线b,交直线a于点M.当点N在什么位置的时候,AM+MN+NB的值最小?
A
B
a
b
M
N
新知探究
A
B
M
N
a
b
(1)由于河岸宽度是固定的,因此当AM+NB最小时,AM+MN+NB最小.问题可转化为:当点N在直线b的什么位置时,AM+NB最小?
新知探究
(2)如图,将AM沿与河岸垂直的方向平移,点M移动到点N,点A移动到点A′,则AA′=MN,AM+NB=A′N+NB.
问题转化为:当点N在直线b的什么位置时,A′N+NB最小?
A
B
M
N
a
b
A′
新知探究
(3)如图,在连接A′,B两点的线中,线段A′B最短.因此,线段A′B与直线b的交点N的位置即为所求.
A
B
M
N
a
b
A′
你能证明此时AM+MN+NB最小吗?
新知探究
在直线b上另外任意取一点N′,过点N′作N′M′⊥a,垂足为M′,连接AM′,A′N′,N′B,证明AM+MN+NB<AM′+M′N′+N′B.
A
B
M
N
a
b
A′
M′
N′
新知探究
证明:在△A′N′B中,
∵A′B<A′N′+BN′,
∴A′N+BN+MN<AM′+BN′+M′N′.
∴AM+MN+BN<AM′+M′N′+BN′.
即AM+MN+BN最小.
N′
A
B
M
N
a
b
A′
M′
归纳总结
1.实际问题用数学语言表达.
2.利用平移,实现线段的转移.
3.把已知问题转化成容易解决的问题.
4.用符号语言进行推理和表达.
归纳总结
最短路径问题
造桥选址问题
练习
归纳总结
化归思想.
利用轴对称、平移等变化,把已知问题转化为容易解决的问题.
两点之间,线段最短.
依据
方法
思想
针对训练
作法:1.将点 沿直线 方向平移至 ,使得 .
3.连接 ,与直线 交于一点即为所求点 .
2.作 关于直线 的对称点 .
4.在点 左侧取点 ,使得 ,即为所求点 .
1.已知线段 ,点 在直线 的同侧,在直线 上求作两点 ,(点 在点 的左侧)且 ,使得四边形 的周长最小.
针对训练
2.如图,荆州古城河在CC′处直角转弯,河宽相同,从A处到B处,须经两座桥:DD ′,EE ′(桥宽不计),设护城河以及两座桥都是东西、南北方向的,怎样架桥可使ADD ′E ′EB的路程最短?
A
D
D ′
C
C′
E
E′
B
针对训练
解:作AF⊥CD,且AF=河宽,作BG ⊥CE,且BG=河宽,连接GF,与河岸相交于E ′,D′.作DD′,EE′即为桥.
理由:由作图法可知,AF//DD′,AF=DD′,则四边形AFD′D为平行四边形,于是AD=FD′,
同理,BE=GE′,
由两点之间线段最短可知,GF最小.
A
D ′
C
C′
E
E′
B
F
G
D
课堂总结
解决最短路径问题的方法
在解决最短路径问题时,我们通常利用轴对称、平移等变换把未知问题转化为已解决的问题,从而作出最短路径的选择.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
