等腰三角形[上学期]
图片预览




文档简介
学科:数学
教学内容:等腰三角形
新课指南
1.知识与技能:(1)经历获得知识的过程,并通过观察、分析、想象、探索,掌握等腰三角形的性质及判定;(2)了解等边三角形的性质和判定等知识的形成过程,培养丰富的想像力,增强审美意识.
2.过程与方法:经历探索等腰(边)三角形的性质及判定,探索应用等腰三角形知识解决实际问题,尤其是用轴对称的性质来解释等腰(或等边)三角形的相关性质,进一步体会从一般到特殊,再从特殊到一般的研究事物的辩证方法.
3.情感态度与价值观:培养学生合作交流、体验成功、体验审美、增强自信心,同时,充分体会分类讨论数学思想在解决问题中的广泛应用.
4.重点与难点;重点是等腰三角形的性质和判定.难点是由轴对称知识来理解和掌握等腰三角形的性质和判定.
教材解读 精华要义
数学与生活
如图14-61所示,位于在海上A,B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B,如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
思考讨论 如果两艘船以同样的速度同时出发,并且同时赶到出事地点,说明两艘船的航程相同,即OA=OB,而已知∠A=∠B,能直接由此判断出OA=OB吗?
知识详解
知识点1 等腰三角形的概念
有两条边相等的三角形,叫做等腰三角形,相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.
如图14-62所示,在△ABC中,若AB=AC,则△ABC是等腰三角形,其中AB,AC叫做腰,BC叫做底边,∠A叫做顶角,∠B和∠C叫做底角.
知识点2 等腰三角形的性质
性质1:等腰三角形的两个底角相等(简写成“等边对等角”).
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
【说明】 等腰三角形的两个性质都可以由证明两个三角形全等而证实.
例如:如图14-63所示,在△ABC中,AB=AC.求证∠B=∠C.
证明:过点A作BC边上的中线AD.
∴BD=DC.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
∴∠B=∠C(全等三角形的对应角相等).
探究交流
上例中并没有直接全等的三角形,而是通过作辅助线“BC边上的中线AD”来构造出两个全等的三角形,再用全等三角形的性质证明出“∠B=∠C”.想一想,本题还有没有作其他辅助线的方法?在本题中能否进一步证明AD是∠BAC的平分线和BD边上的高?试试看.
点拨 由等腰三角形的性质2可知,等腰三角形是轴对称图形,它的对称轴是底边上的中线(顶角平分线、底边上的高)所在直线.
知识点3 等腰三角形的判定定理
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
例如:图14-64所示,在△ABC中,∠B=∠C.求证AB=AC.
证明:作AD⊥BC,垂足为D.
∴∠ADB=∠ADC=90°.
在Rt△ADB和Rt△ADC中,
∴Rt△ADB≌Rt△ADC(AAS).
∴AB=AC(全等三角形的对应边相等).
知识点4 等边三角形的概念
三条边都相等的三角形,叫做等边三角形.
知识点5 等边三角形的性质和判定
Ⅰ.等边三角形的性质和判定.
(1)等边三角形的三个内角都相等,并且每一个内角都等于60°
(2)三个角都相等的三角形是等边三角形
(3)有一个角是60°的等腰三角形是等边三角形
Ⅱ.在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半.
典例剖析 师生互动
基础知识应用题
本节知识的基础应用主要包括:(1)等腰三角形的性质和判定;(2)等边三角形的性质;(3)三角形的内角和;(4)三角形三边关系.
例1 已知三角形的一个内角是110°,求另外两个角的度数.
(分析)因为等腰三角形的内角和是180°,若110°是底角,则110°×2=220°>180°,所以110°只能是顶角.故底角是=35°.
解:由题意可知,110°是顶角,设底角为α,则
2α+110°=180°,∴α=35°.
∴这个三角形另外两个角是35°,35°.
例2 等腰三角形的一个内角是80°,求它的另外两个角.
(分析)用分类讨论的思想方法来思考本题.若顶角是80°,则设底角为α,由三角形内角和得2α+80°=180°,∴α=50°.若底角是80°则设项角为β,由三角形内角和得2×80°+β=180°,∴β=20°.
解:①若顶角是80°,设底角为α,则有
2α+80°=180°,
∴α=50°.
②若底角是80°,设顶角为β,则有
80°×2+β=180°,
∴β=20。
∴这个等腰三角形的另外两个角是50°,50°或80°,20°.
学生做一做 (1)若等腰三角形的一个内角为40°,则它的顶角为 ;
(2)若等腰三角形的两个内角和为100°,则它的顶角为 .
老师评一评 (1)只告诉一个内角为40°,并没有说明是哪一个内角,所以应分两种情况来讨论:若顶角为40°,则40°+2α=180°,α=70°。符合要求,直接填上即可;若底角为40°,则顶角为180°-2×40°=100°,符合要求.∴应填40°或100°.
(2)已知两个内角的和为100°,三角形的内角和为180°,所以可知等腰三角形一个内角为180°-100°=80°,同样用分类讨论方法来考虑:若80°是顶角,可直接填上即可;若80°是底角,则顶角是100°-80°=20°.∴应填80°或20°.
例3 等腰三角形的底角与顶角的度数之比为2∶1,则顶角为( )
A.72° B.36° C.36°或72° D.18°
(分析) 设顶角为α,则底角为2α,由三角形的内角和可知,α+2×2α=180°,5α=180°,∴α=36°,∴这个三角形的顶角为36°,故正确答案为B项.
例4 若等腰三角形的底边长是8cm,腰长是5cm,则这个等腰三角形的周长是( )
A.21cm B.18cm C.18cm或21cm D.13cm或26cm
(分析)由题意可知,8+5+5=18(cm),故正确答案为B项.
学生做一做 等腰三角形一边长为8,另一边长为4,则它的周长为 .
老师评一评 题中给出等腰三角形的两边长分别是8和4,但并没有给出哪一个是腰,哪一个是底,要分两种情况:
①若腰是8,底是4,则另一腰是8,有4+8>8,满足三角形三边关系,∴8×2+4=20;
②若腰是4,底是8,则另一腰是4,有4+4=8,不满足三角形三边关系,∴这种情况不存在.
∴这个三角形的周长为20.
小结 已知等腰三角形两边,求第三边或周长时,要全面考虑第三边的情况,求出第三边要满足三角形的三边关系,所以上题可以这样考虑:
设这个等腰三角形的第三边为x,由三角形三边关系可知,
8-4<x<8+4,
即4<x<12,
又因为这个三角形是等腰三角形,所以第三边只能考虑4或8,
由4<x<12,∴x=8,
∴这个三角形的第三边为8,其周长为8×2+4=20.
例5 如果等腰三角形的三边长均为整数,且它的周长为10cm,那么它的三边长分别为.
.
(分析)设这个三角形的腰长为xcm,则底边长为10-2x=2(5-x)cm.
共有4种情况:①当x=1cm时,10-2x=8(cm);
②当x=2cm时,10-2x=6(cm);
③当x=3cm时,10-2x=4(cm);
④当x=4cm时,10-2x=2(cm).
又由三角形三边关系可知,①②不满足三角形三边关系.
∴这个三角形的三边有两种;
3cm,3cm,4cm或4cm,4cm,2cm.
答案:3cm,3cm,4cm或4cm,4cm,2cm
综合应用题
本节知识的综合应用主要包括:(1)等腰(边)三角形的性质和判定的综合应用;(2)与方程、不等式知识的综合应用;(3)与三角形全等的综合应用.
例6 如图14-65所示,在△ABC中,AB=AC=CD,AD=DB,求∠BAC的度数.
(分析)本题由已知条件知,图中的三个三角形都是等腰三角形,相等的角或有关系的角较多,为了明确它们之间的关系,这类题往往要设其中一个角为α,然后利用α将其余的角表示出来.
解:∵AB=AC=CD,AD=DB
∴∠1=∠2,∠B=∠3,∠B=∠C.
设∠B=α,则∠B=∠3=∠C=α,∠1=∠2=∠3+∠B=2α.
在△ABC中,∠B+∠C+∠1+∠3=180°,
即α+α+2α+α=180°,
5α=180°,α=36°.
∴∠BAC=∠3+∠1=α+2α=3α=3×36°=108°.
∴∠BAC的度数为108°.
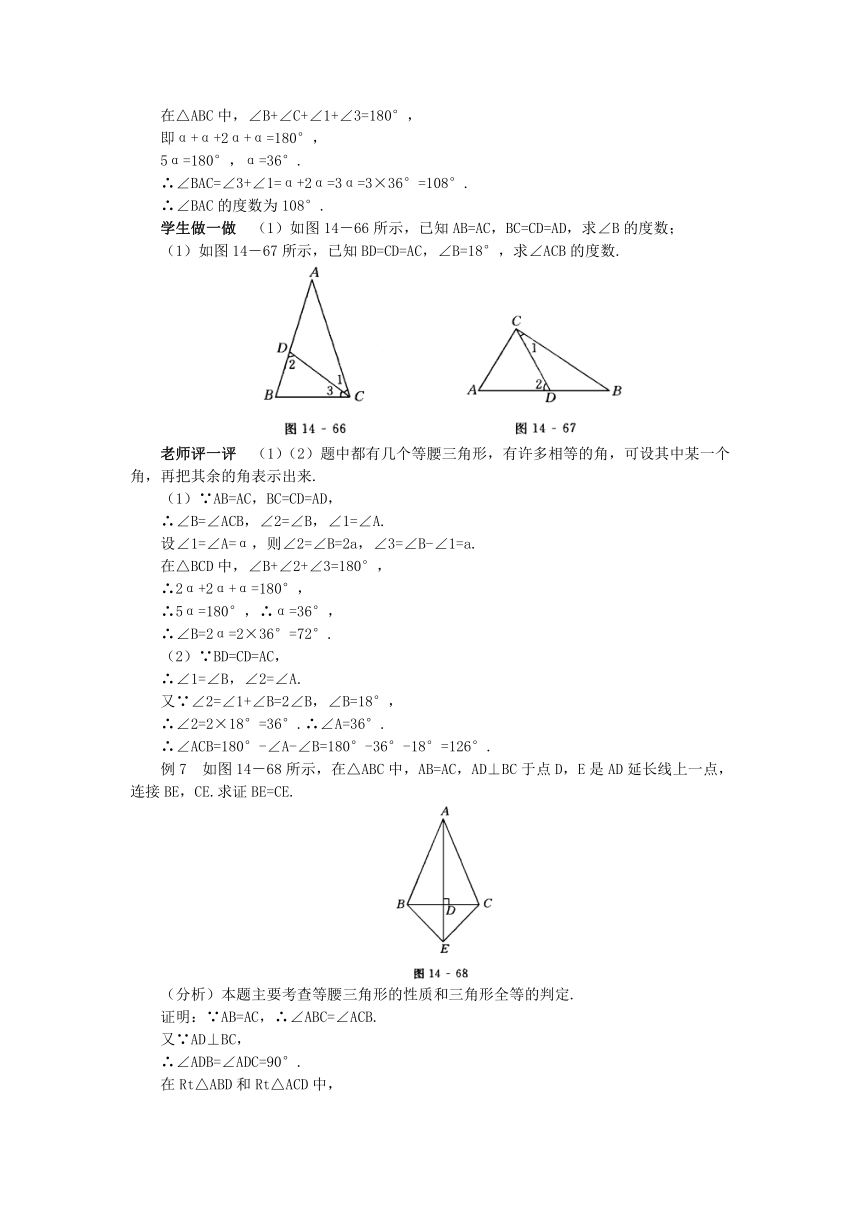
学生做一做 (1)如图14-66所示,已知AB=AC,BC=CD=AD,求∠B的度数;
(1)如图14-67所示,已知BD=CD=AC,∠B=18°,求∠ACB的度数.
老师评一评 (1)(2)题中都有几个等腰三角形,有许多相等的角,可设其中某一个角,再把其余的角表示出来.
(1)∵AB=AC,BC=CD=AD,
∴∠B=∠ACB,∠2=∠B,∠1=∠A.
设∠1=∠A=α,则∠2=∠B=2a,∠3=∠B-∠1=a.
在△BCD中,∠B+∠2+∠3=180°,
∴2α+2α+α=180°,
∴5α=180°,∴α=36°,
∴∠B=2α=2×36°=72°.
(2)∵BD=CD=AC,
∴∠1=∠B,∠2=∠A.
又∵∠2=∠1+∠B=2∠B,∠B=18°,
∴∠2=2×18°=36°.∴∠A=36°.
∴∠ACB=180°-∠A-∠B=180°-36°-18°=126°.
例7 如图14-68所示,在△ABC中,AB=AC,AD⊥BC于点D,E是AD延长线上一点,连接BE,CE.求证BE=CE.
(分析)本题主要考查等腰三角形的性质和三角形全等的判定.
证明:∵AB=AC,∴∠ABC=∠ACB.
又∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在Rt△ABD和Rt△ACD中,
∴Rt△ABD≌Rt△ACD(HL).
∴∠BAD=∠CAD(全等三角形的对应角相等).
在△ABE和△ACE中,
∴△ABE≌△ACE(SAS).
∴BE=CE(全等三角形的对应边相等).
例8 如图14-69所示,在△ABC中,AB=AC,AE是∠BAC外角∠DAC的平分线.试判断AF与BC的位置关系.
(分析)主要考查等腰三角形性质的应用.
解:AE与BC的位置关系是AE∥BC.理由如下:
∵AB=AC,∴∠B=∠C.
又∵∠DAC=∠B+∠C=2∠C,AE是∠DAC的平分线;
∴2∠EAC=∠DAC,
∴∠C=∠EAC,
∴AE∥BC(内错角相等,两直线平行).
学生做一做 (1)如图14-69所示,在△ABC中,AB=AC,AE∥BC.求证AE是△BAC的外角∠DAC的平分线;
(2)如图14-69所示,在△ABC中,AE是∠BAC的外角∠DAC的平分线,且AE∥BC.试判断△ABC的形状.
老师评一评 本题意在考查如果把已知问题中的条件与结论互换,看得到的新命题是否成立,有利于培养学生灵活分析问题和解决问题的能力.
(1)∵AB=AC,∴∠B=∠C.
又∵AE∥BC,∴∠EAC=∠C(两直线平行,内错角相等),
∠DAE=∠B(两直线平行,同位角相等).
∴∠EAC=∠DAE.
∴AE是∠DAC的平分线.
(2)△ABC是等腰三角形.理由如下:
∵AE是∠DAC的平分线,
∴∠DAE=∠EAC.
又∵AE∥BC,
∴∠DAE=∠B,∠EAC=∠C,
∴∠B=∠C,
∴AB=AC(等角对等边).
∴△ABC是等腰三角形.
例9 如图14-70所示,△ABD和△ACE是等边三角形.求证BE=CD.
(分析)欲证BE=CD,只需证明△ADC≌△ABE即可.
证明:∵△ABD和△ACE是等边三角形,
∴∠DAB=∠EAC=60°,
AD=AB,AC=AE
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠BAE.
在△DAC和△BAE中,
∴△DAC≌△BAE(SAS).
∴DC=BE(全等三角形的对应边相等).
学生做一做 如图14-71所示,B,C,D三点在一条直线上,△ABC和△ECD是等边三角形.求证BE=AD.
老师评一评 欲证BE=AD,只需证明△BCE≌△ACD即可.
∵△ABC和△ECD是等边三角形,
∴∠ACB=∠ECD=60°,BC=AC,EC=CD.
∴∠ACB+∠ACE=∠ECD+∠ACE,
即∠BCE=∠ACD.
在△BCE和△ACD中,
∴△BCE≌△ACD(SAS).
∴BE=AD(全等三角形的对应边相等).
小结 在完成类似的几何问题时,要注意灵活,举一反三,这样就可以避免题海战术,能够以点代面,同一类问题研究透彻,类似问题便能迎刃而解.
例10 等腰三角形ABC的周长为10cm,底边BC长为ycm,腰AB长为xcm.
(1)写出y关于x的函数关系式;
(2)求x的取值范围;
(3)求y的取值范围.
(分析)本题主要考查代数与几何知识的综合应用,解题时注意相关的几何知识.
解:(1)y=10-2x.
(2)∵x,y为线段,∴x>0,y>0.
∴10-2x>0,∴O<x<5.①
又∵x,y为三角形边长,
∴x+x>y,即2x>10-2x.②
由①②可得2.5<x<5.
∴x的取值范围是2.5<x<5.
(3)∵2.5<x<5,∴5<2x<10,∴-10<-2x<-5,∴O<10-2x<5,
∴O<y<5.
∴y的取值范围是O<y<5.
例11 如图14-72所示,在△ABC中.AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.
图14-72
解:∵AB=AC,∴∠ABC=∠C.
又∵∠A+∠ABC+∠C=180°,
∴∠C=(180°-∠A)=90°-∠A.
又∵BD⊥AC.∴∠BDC=90°.
∴∠DBC=90°-∠C=90°-(90°-∠A)=∠A,
∴∠DBC=∠A.
即等腰三角形腰上的高与底边的夹角等于该等腰三角形顶角的一半.
学生做一做 (1)在△ABC中,AB=AC,BD⊥AC,垂足为D,若∠DBC=25°,则∠A= ;
(2)在△ABC中,AB=AC,若∠B=70°,BD⊥AC,垂足为D,则∠DBC= .
老师评一评 由例11的结论得出;(1)题中,∠DBC=25°=∠A,∴∠A=50°.(2)题中,∵AB=AC,∴∠B=∠C=70°.∴∠A=40°.∴∠DBC=20°.
例12 如图14-73所示,在△ABC中,∠C=90°,∠BAC=60°,AB的垂直平分线交AB于D,交BC于E,若CE=3cm,求BE的长.
(分析)主要应用线段垂直平分线的性质和30°角的直角三角形的性质.
解:连接AE,
∵∠C=90°,∠BAC=60°,
∴∠B=30°.
又∵DE是AB的垂直平分线,
∴EA=EB.∴∠EAB=∠B=30°.
∴∠CAE=30°.
∴AE是∠CAB的平分线.
又∵∠C=90°,ED⊥AB,
∴DE=EC=3cm.
在Rt△DBE中,∠B=30°,∠EDB=90°,
∴DE=BE,∴BE=2×3=6(cm).
学生做一做 如图14-74所示,在Rt△ABC中,∠C=90°,∠B=15°,AB的垂直平分线分别与BC,AB交于M,N.求证MB=2AC.
老师评一评 连接MA,
∴∠C=90°,∠B=15°,
∴∠CAB=75°.
又∵MN是AB的垂直平分线,
∴MA=MB.
∴∠MAB=∠B=15°.
∴∠CAM=∠CAB-∠MAB=75°-15°=60°.
∴∠CMA=30°.
在Rt△CMA中,∠C=90°,∠CMA=30°,
∴CA=MA.∴CA=MB.
即MB=2AC.
小结 在直角三角形中证明线段的一半或2倍关系时,经常考虑30°角所对的直角边.
探索与创新题
主要考查:(1)利用等腰三角形知识探索和创新的能力;(2)图形分割;(3)辅助线的灵活应用;(4)探讨结论性问题等。
例13 如图14-75所示,已知点O是∠ABC,∠ACB的平分线的交点,且OD∥AB,OE∥AC.
(1)图形中共有哪几个等腰三角形?选一者证明之;
(2)试说明△ODE的周长与BC的关系;
(3)若BC=12cm,则△ODE的周长 .
(分析)本题(1)问主要是等腰三角形的判定;(2)问是探讨两者间的数量关系,由(1)可得;(3)问由(2)问的结果得出.
解:(1)图形中共有两个等腰三角形,它们分别是△OBD和△OCE.
以△OBD为例.
∵BO平分∠ABC,∴∠1=∠2.
又∵OD∥AB,∴∠1=∠3.
∴∠2=∠3.∴DB=OD.
∴△OBD是等腰三角形.
(2)由(1)可知,DB=DO.同理EO=EC.
∴△ODE的周长=OD+DE+EO=DB+DE+EC=BC.
∴△ODE的周长与BC的关系是:△ODE的周长=BC.
(3)由(2)可知,△ODE的周长=BC.
又∵BC=12cm,
∴△ODE的周长=12cm.
学生做一做 如图14-76所示,在△ABC中,BO,CO分别为∠ABC,∠ACB的平分线,经过点O的直线DE∥BC,交AB于点D,交AC于点E.
(1)图中等腰三角形分别是 ;
(2)DE与BD+EC的关系是:BD= .
老师评一评 欲证等腰三角形,需证角相等.
(1)∵DE∥BC,∴∠DOB=∠OBC.
又∵BO平分∠ABC,∴∠ABO=∠OBC.
∴∠DOB=∠ABO.∴DB=DO.
∴△DBO是等腰三角形.
同理EO=EC.
∴△EOC是等腰三角形.
(2)DE=DO+OE=BD+EC,
∴DE=BD+EC.
例14 如图14-77所示,在△ABC中,∠ACB=90°,BD=BC,AE=AC.试问:∠DCE是否与∠A有关?如果无关,求∠DCE的大小.
解:∠DCE与∠A无关,∠DCE=45°.理由如下:
∵BD=BC,∴∠BDC=∠BCD.
∴∠BDC=(180°-∠B)=90°-∠B.
又∵AE=AC,∴∠AEC=∠ACE.
∴∠AEC=(180°-∠A)=90°-∠A.
∴∠AEC+∠BDC=(90°-∠A)+(90°-∠B)
=180°-(∠A+∠B).
又∵∠ACB=90°,
∴∠BDC+∠AEC=180°-×90°=135°.
∴∠BDC+∠AEC=135°.
∴∠DCE=45°.
例15 如图14-78所示,在△ABC中,AD⊥BC于D,∠B=2∠C.求证AB+BD=CD.
(分析)如何利用条件∠B=2∠C,又如何得到AB+BD,不同的思考方向,会找到不同的解题方法.
证明:在CD上截取DE=DB,连接AE,
∵AD⊥BC,∴AE=AB.
∴∠B=∠AEB.
又∵∠AEB=∠C+∠CAE=2∠C,
∴∠CAE=∠C.∴AE=EC.
∴AB+BD=AE+BD=EC+ED=CD.
∴AB+BD=CD.
例16 (2003·杭州)如图14-79所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若OC=4,则PD等于( )
A.4 B.3 C.2 D.1
(分析)本题中有角平分线、平行线,这是等腰三角形的重要形成条件,另外,PD⊥OA于D,显然需要作另外一个垂直,这是角平分线性质的一个重要应用.
如图14-80所示,
过点P作PE⊥OB于E.
又∵OP平分∠BOA,PD⊥OA于D.
∴PD=PE.
∵PC∥OA,∴∠2=∠3.
又∵∠1=∠2,∠1=15°,
∴∠3=15°,CO=CP.
∴∠4=∠1+∠3=2∠1=15°×2=30°.
在Rt△CPE中,∠4=30°,∠CEP=90°,
∴PE=PC=OC=×4=2.
∴PD=2,故正确答案为C项.
学生做一做 如图14-81所示,已知矩形ABCD,沿对角线AC把△DAC翻折,AD′与BC相交于点E.判断△AEC的形状.
老师评一评 △AEC是等腰三角形,关键是证明∠EAC=∠ECA.
理由如下:
由题意可知,△ADC≌△AD′C,
∴∠DAC=∠D′AC.
又∵AD∥BC,∴∠DAC=∠ACE.
∴∠D′AC=∠ACE.∴EA=EC.
∴△EAC是等腰三角形.
小结 (1)证明线段相等是最基本的几何问题,目前常用证法有:
①若两条线段属于两个三角形,则考虑对应的三角形全等;
②若两条线段是同一个三角形两边,则考虑用等角对等边证明;
③寻找中间线段,通过等量代换来证明.
(2)类似地,我们可以对证明角相等,等边三角形的判定作归纳总结.
在证明等腰三角形时,常需应用作辅助线构造全等三角形,进而应用等腰三角形的性质为题目服务,常用的构造方法有:
①“角平分线+平行线”构造等腰三角形;
②“角平分线+垂线”构造等腰三角形;
③用“垂直平分线”构造等腰三角形;
④用“三角形中角的2倍关系”构造等腰三角形.
中考展望 点击中考
中考命题总结与展望
这部分内容在中考中多以填空、选择的形式出现,在综合题中,等腰三角形的性质和判定的知识较为常见。
中考试题预测
例1 (2004·黄冈)如图14-82所示,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证BF=2CF.
(分析)证线段2倍关系,通常考虑在直角三角形中是否有30°角.
证明:如图14-83所示,连接AF,
∵AB=AC,∠BAC=120°,
∴∠B=∠C==30°.
又∵EF是AC的垂直平分线,
∴FA=FC.∴∠C=∠FAC=30°,
∴∠BAF=∠BAC-∠FAC=120°-30°=90°.
在Rt△BAF中,∠BAF=90°,∠B=30°,
∴AF=BF.∴CF=BF.
∴BF=2CF.
例2 (2004·四川)如图14-84所示,D是△ABC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且BF=CE.求证:
(1)△ABC是等腰三角形;
(2)当∠A=90°时,试判断四边形AFDE是什么形状的四边形.
(分析)(1)只需证△BFD≌△CED,证∠B=∠C即可.
(2)只需证邻边相等,因为邻边相等的长方形是正方形.
证明:(1)∵DF⊥AB,DE⊥AC,
∴∠BFD=∠CED=90°.
又∵D是BC的中点,∴BD=CD.
在Rt△BFD和Rt△CED中,
∴Rt△BFD≌Rt△CED(HL).
∴∠B=∠C(全等三角形的对应角相等).
∴AB=AC(等角对等边).
∴△ABC是等腰三角形.
解:(2)当∠A=90°时,四边形AFDE是正方形.
理由如下:
∵∠AFD=∠AED=∠A=90°,
∴四边形AFDE是长方形.
由(1)知△BFD≌△CED,∴FD=ED.
∴四边形AFDE是正方形.
例3 (2004·陕西)如图14-85所示,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高,且CD,BE交于一点P,若∠A=50°,则∠BPC的度数是( )
A.150° B.130° C.120° D.100°
(分析)本题主要考查:(1)直角三角形两锐角互余;(2)三角形内角和是180°.具体过程如下:
∵BE⊥AC,CD⊥AB,
∴∠AEB=∠ADC=90°.
又∵∠A=50°,
∴∠ABE=∠ACD=90°-50°=40°.
又∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°.
∴∠PBC+∠PCB=(∠ABC+∠ACB)-(∠ABE+∠ACD)
=130°-(40°+40°)=50°.
∴∠BPC=180°-(∠PBC+∠PCB)=180°-50°=130°.
∴∠BPC=130°.故正确答案为B项.
例4 (中考预测题)如图14-86所示,在梯形ABCD中,AB=AD,AD∥BC,∠A=100°,试求∠DBC的度数.
(分析)本题要求一个角的度数,已知条件中的AD∥BC恰与角有密切联系,所以应该充分利用.
解:由AD=AB知,∠ADB=∠ABD(等腰三角形的底角相等),由AD∥BC知,∠ADB=∠DBC(两直线平行,内错角相等).
可见∠ABD=∠DBC.
而∠A+∠ABC=180°(两直线平行,同旁内角互补),
∠A=100°,所以100°+2∠DBC=180°.
可以得出∠DBC=40°.
例5 (2004·青海)如图14-87所示,把一张平行四边形纸片ABCD沿BD对折,使C点落在E处,BE与AD相交于点O,若∠DBC=15°,则∠BOD= .
(分析)由题意可知△BDC≌△BDE.
∴∠DBC=∠DBE.
又∵AD∥BC,∴∠ODB=∠DBC.
∴∠OBD=∠ODB.
又∵∠DBC=15°,
∴∠OBD=∠ODB=15°.
∴∠BOD=180°-15°×2=150°.
课堂小结 本节归纳
本节主要学习了:
(1)等腰三角形的概念、性质和判定;
(2)等边三角形的概念、性质和判定;
(3)直角三角形(有一个角是30°的直角三角形)的性质.
习题选解 课本习题
课本第149~151页
习题14.3
1.(1)35°,35°(2)80°,20°或50°,50°
2.证明:∵AD∥BC,∴∠ADB=∠DBC.
又∵BD平分∠ABC,∴∠ABD=∠DBC.
∴∠ADB=∠ABD,∴AB=AD(等角对等边).
3.解:∵五角星的五个角都是顶角为36°的等腰三角形,
∴每个底角的度数是(180°-36°)=72°.
∴∠AMB=180°-72°=108°.
4.解:∵AB=AC,∠BAC=100°,
∴∠B=∠C=×(180°-100°)=40°.
又∵AD⊥BC,∴AD是∠BAC的平分线,
∴∠BAD=∠CAD=×100°=50°.
5.解:△ECB是等腰三角形.理由如下:
∵CE∥AD,∴∠A=∠CEB.
又∵∠A=∠B,∴∠CEB=∠B.∴CE=CB.
∴△CBE是等腰三角形.
6.证明:∵AB=AC,∴∠B=∠C.
又∵AD=AE,∴∠ADE=∠AED.
∴∠ADB=∠AEC.
在△ABD和△ACE中,
∴△ABD≌△ACE(AAS)
∴BD=CE(全等三角形的对应边相等).
7.解:∵AB=AC,∠A=40°,
∴∠ABC=∠C=×(180°-40°)=70°.
又∵MN是AB的垂直平分线,∴DA=DB.
∴∠A=∠DBA=40°.
∴∠DBC=∠ABC-∠ABD=70°-40°=30°.
9.解:∵∠PAB=∠PBA,∴PA=PB.这是利用了等腰三角形的判定
10.解:∵∠NBC=84°,∠NAC=42°,∠NBC=∠NAC+∠C,
84°=42°+∠C,∴∠C=42°.∴BC=BA.
又∵BA=15×(10-8)=30(海里),
∴BC=30海里.
即从海岛B到灯塔C的距离是30海里.
11.证明:∵△ABD,△AEC都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠EAC=60°.
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠BAE.
在△ADC和△ABE中,
∴△ADC≌△ABE(SAS).
∴DC=BE.
12.解:等腰三角形两底角的平分线相等,等腰三角形两腰上的中线相等,等腰三角形两腰上的高相等.以等腰三角形两腰上的高相等为例证明.
已知:如图14-88所示,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D,E.
求证:BD=CE.
证明:∵AB=AC,∴∠ABC=∠ACB.
又∵BD⊥AC,CE⊥AB,∴∠BEC=∠CDB=90°.
在Rt△BCE和Rt△CBD中,
∴Rt△BCE≌Rt△CBD(AAS).
∴BD=CE(全等三角形的对应边相等).
13.提示:(1)∠ECD=∠EDC;(2)OC=OD;(3)OE是CD的垂直平分线.
理由如下:
∵OE平分∠AOB,ED⊥OB,EC⊥OA,垂足分别为D,C,
∴ED=EC.∴∠EDC=∠ECD.
在Rt△ODE和Rt△OCE中,
∴Rt△ODE≌Rt△OCE(HL).
∴OD=OC.∴△ODC是等腰三角形.
又∵OE是∠DOC的平分线,
∴OE是底边CD上的高和中线.
即OE是线段DC的垂直平分线.
14.解:如图14-89所示.
作法如下:作∠CAB的平分线AD,交于BC于点D,再作DE上AB,垂足为E.
∵∠C=90°,∠B=30°,
∴∠CAB=60°.∴∠1=∠2=30°.
又∵DE⊥AB,∠C=90°,∴∠C=∠AED=90°.
在Rt△ACD和Rt△AED中,
∴Rt△ACD≌Rt△AED(AAS).
又∵∠2=∠B=30°,∴DA=DB.
又∵DE⊥AB,∴∠AED=∠BED=90°.
在Rt△ADE和Rt△BDE中,
∴Rt△ADE≌Rt△BDE(AAS).
∴Rt△ADC≌Rt△ADE≌Rt△BDE.
自我评价 知识巩固
1.等边三角形的两条中线所成的钝角的度数是( )
A.120° B.130° C.150° D.160°
2.设等腰三角形的顶角为∠A,则∠A的取值范围是( )
A.0°≤∠A<180° B.0°<∠A<180°
C.0°≤∠A<180° D.0°<∠A<90°
3.一个三角形的外角分别是135°,90°,135°,则这个三角形是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
4.如果等腰三角形一底角为α,那么( )
A.α≤45° B.0°<α<90° C.α≤90° D.90°<α<180°
5.等腰三角形一腰上的高与底边所成的角等于( )
A.顶角 B.顶角的一半 C.顶角的2倍 D.底角的一半
6.如图14-90所示,在△ABC中,AB=AC,BD,CE是角平分线,图中的等腰三角形共有( )
A.6个 B.5个 C.4个 D.3个
7.如图14-91所示,在△ABC中,BO平分∠ABC,CO平分∠ACB,MN∥BC,MN经过点O,若AB=12,AC=18,则△AMN的周长是( )
A.15 B.18 C.24 D.30
8.如图14-92所示,O是∠ABC,∠ACB的平分线的交点,OD∥AB,交BC于D,OE∥AC交BC于E,若BC=10cm,则面DOE的周长为( )
A.8cm B.9cm C.10cm D.11cm
9.在△ABC中,若AB=AC,∠A=90°,则∠B= ,∠C= .
10.如果一个三角形的两个内角分别为70°,40°,那么这个三角形是 .
11.在△ABC中,AB=AC,∠A=60°,则∠B= ,∠C= ,△ABC是 三角形.
12.已知等腰三角形的一个底角等于顶角的2倍,这个等腰三角形各角的度数分别是 .
13.如图14-93所示,BD是△ABC的角平分线,∠A=36°,∠C=72°,则图中共有 个等腰三角形,它们分别是 .
14.(1)如果等腰三角形的两边长分别是4cm,7cm,那么它的周长是 ;
(2)如果等腰三角形的两边长分别是5cm和10cm,则这个等腰三角形的周长是 .
15.等腰三角形两腰上的高、中线,两底角平分线分别 .
16.在等腰三角形中,如果顶角是一个底角的2倍,那么这个三角形是 三角形.
17.若三角形是轴对称图形,且有一个角是60°,则这个三角形是 三角形.
18.一个等腰三角形的周长为18cm,一边长为4cm,求其他两边的长.
19.如图14-94所示,在△ABC中,AB=AC,DE∥BC,交AB于D,交AC于E,求证△ADE也是等腰三角形.
20.如图14-95所示,四边形ABCD中,AD∥BC,AB=AD,试证明BD是∠ABC的平分线.
21.如图14-96所示,∠1=∠2,BD=CD,试证明△ABC是等腰三角形.
22.在△ABC中,AB=AC,CD为底边上的高,△ABC的周长为16cm,△ABD的周长为12cm,求AD的长.
23.如图14-97所示,CE是△ABC的角平分线,过点E画BC的平行线,交AC于点D,交外角∠ACG的平分线于点F.试证明DE=DF.
24.(1)如图14-98所示,∠BAC=90°,AD⊥BC,垂足为D,BE平分∠ABC,交AC于E,交AD于F.试判断△AEF的形状,并说明理由;
(2)如图14-98所示,已知∠BAC=90°,AD⊥BC,垂足为D,AE=AF.试说明BE平分∠ABC.
参考答案
1.A 2.B 3.D 4.B 5.B 6.A 7.D 8.C 9.45°,45° 10.等腰三角形
11.60° 60° 等边 12.36°,72°,72° 13.3 △ABC,△ ABD,△BCD
14.(1)15cm或18cm (2)25cm 15.相等 16.等腰直角 17.等边
18.提示:分两种情况讨论:
①若以4cm为底边长,设腰长为xcm,
则有4+2x=18,∴x=7.
∴另外两边的长为7cm,7cm.
②若以4cm为腰长,设底边长为ycm,则有
4×2+y=18,∴y=10.
∴4+4<10,不满足三角形的三边关系,
∴4cm,4cm,10cm不能组成三角形.
∴三角形的另外两条边长为7cm,7cm.
19.证明:∵AB=AC,∴∠B=∠C.
又∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.
∴∠ADE=∠AED.∴AD=AE.
∴△ADE是等腰三角形.
20.证明:∵AD∥BC,∴∠ADB=∠DBC.
又∵AB=AD,∴∠ABD=∠ADB.
∴∠DBC=∠ABD.
∴BD是∠ABC的平分线.
21.证明:∵BD=DC,∴∠DBC=∠DCB.
又∵∠1=∠2,
∴∠DBC+∠1=∠DCB+∠2,
即∠ABC=∠ACB.∴AB=AC.
∴△ABC是等腰三角形.
22.解:如图14-99所示.
∵AB=AC,AD为BC边上的高,
∴BD=DC.
又∵△ABD的周长为12cm,△ABC的周长为16cm,
∴AB+BD=16÷2=8(cm).
AB+BD+AD=12(cm).
∴AD=12-8=4(cm).
23.证明:∵CE是∠ACB的平分线,∴∠ACE=∠ECB.
又∵EF∥BC,∴∠DEC=∠ECB.
∴∠ACE=∠DEC.∴DE=DC.
同理DF=DC.∴DE=DF.
24.解:(1)如图14-100所示.
∵BE平分∠ABC,∴∠1=∠2.
又∵∠BAC=90°,AD⊥BC,
∴∠3=90°-∠1,∠4=90°-∠2,∴∠3=∠4.
又∵∠4=∠5,∴∠3=∠5,∴AE=AF.
∴△AEF是等腰三角形.
(2)如图14-101所示.
∵AE=AF,∴∠1=∠2.
又∵∠1=∠3,∴∠2=∠3.
又∵∠BAC=90°,AD⊥BC,
∴∠4=90°-∠2,∠5=90°-∠3,∴∠4=∠5.
∴BE是∠ABC的平分线.
教学内容:等腰三角形
新课指南
1.知识与技能:(1)经历获得知识的过程,并通过观察、分析、想象、探索,掌握等腰三角形的性质及判定;(2)了解等边三角形的性质和判定等知识的形成过程,培养丰富的想像力,增强审美意识.
2.过程与方法:经历探索等腰(边)三角形的性质及判定,探索应用等腰三角形知识解决实际问题,尤其是用轴对称的性质来解释等腰(或等边)三角形的相关性质,进一步体会从一般到特殊,再从特殊到一般的研究事物的辩证方法.
3.情感态度与价值观:培养学生合作交流、体验成功、体验审美、增强自信心,同时,充分体会分类讨论数学思想在解决问题中的广泛应用.
4.重点与难点;重点是等腰三角形的性质和判定.难点是由轴对称知识来理解和掌握等腰三角形的性质和判定.
教材解读 精华要义
数学与生活
如图14-61所示,位于在海上A,B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B,如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
思考讨论 如果两艘船以同样的速度同时出发,并且同时赶到出事地点,说明两艘船的航程相同,即OA=OB,而已知∠A=∠B,能直接由此判断出OA=OB吗?
知识详解
知识点1 等腰三角形的概念
有两条边相等的三角形,叫做等腰三角形,相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.
如图14-62所示,在△ABC中,若AB=AC,则△ABC是等腰三角形,其中AB,AC叫做腰,BC叫做底边,∠A叫做顶角,∠B和∠C叫做底角.
知识点2 等腰三角形的性质
性质1:等腰三角形的两个底角相等(简写成“等边对等角”).
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
【说明】 等腰三角形的两个性质都可以由证明两个三角形全等而证实.
例如:如图14-63所示,在△ABC中,AB=AC.求证∠B=∠C.
证明:过点A作BC边上的中线AD.
∴BD=DC.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
∴∠B=∠C(全等三角形的对应角相等).
探究交流
上例中并没有直接全等的三角形,而是通过作辅助线“BC边上的中线AD”来构造出两个全等的三角形,再用全等三角形的性质证明出“∠B=∠C”.想一想,本题还有没有作其他辅助线的方法?在本题中能否进一步证明AD是∠BAC的平分线和BD边上的高?试试看.
点拨 由等腰三角形的性质2可知,等腰三角形是轴对称图形,它的对称轴是底边上的中线(顶角平分线、底边上的高)所在直线.
知识点3 等腰三角形的判定定理
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
例如:图14-64所示,在△ABC中,∠B=∠C.求证AB=AC.
证明:作AD⊥BC,垂足为D.
∴∠ADB=∠ADC=90°.
在Rt△ADB和Rt△ADC中,
∴Rt△ADB≌Rt△ADC(AAS).
∴AB=AC(全等三角形的对应边相等).
知识点4 等边三角形的概念
三条边都相等的三角形,叫做等边三角形.
知识点5 等边三角形的性质和判定
Ⅰ.等边三角形的性质和判定.
(1)等边三角形的三个内角都相等,并且每一个内角都等于60°
(2)三个角都相等的三角形是等边三角形
(3)有一个角是60°的等腰三角形是等边三角形
Ⅱ.在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半.
典例剖析 师生互动
基础知识应用题
本节知识的基础应用主要包括:(1)等腰三角形的性质和判定;(2)等边三角形的性质;(3)三角形的内角和;(4)三角形三边关系.
例1 已知三角形的一个内角是110°,求另外两个角的度数.
(分析)因为等腰三角形的内角和是180°,若110°是底角,则110°×2=220°>180°,所以110°只能是顶角.故底角是=35°.
解:由题意可知,110°是顶角,设底角为α,则
2α+110°=180°,∴α=35°.
∴这个三角形另外两个角是35°,35°.
例2 等腰三角形的一个内角是80°,求它的另外两个角.
(分析)用分类讨论的思想方法来思考本题.若顶角是80°,则设底角为α,由三角形内角和得2α+80°=180°,∴α=50°.若底角是80°则设项角为β,由三角形内角和得2×80°+β=180°,∴β=20°.
解:①若顶角是80°,设底角为α,则有
2α+80°=180°,
∴α=50°.
②若底角是80°,设顶角为β,则有
80°×2+β=180°,
∴β=20。
∴这个等腰三角形的另外两个角是50°,50°或80°,20°.
学生做一做 (1)若等腰三角形的一个内角为40°,则它的顶角为 ;
(2)若等腰三角形的两个内角和为100°,则它的顶角为 .
老师评一评 (1)只告诉一个内角为40°,并没有说明是哪一个内角,所以应分两种情况来讨论:若顶角为40°,则40°+2α=180°,α=70°。符合要求,直接填上即可;若底角为40°,则顶角为180°-2×40°=100°,符合要求.∴应填40°或100°.
(2)已知两个内角的和为100°,三角形的内角和为180°,所以可知等腰三角形一个内角为180°-100°=80°,同样用分类讨论方法来考虑:若80°是顶角,可直接填上即可;若80°是底角,则顶角是100°-80°=20°.∴应填80°或20°.
例3 等腰三角形的底角与顶角的度数之比为2∶1,则顶角为( )
A.72° B.36° C.36°或72° D.18°
(分析) 设顶角为α,则底角为2α,由三角形的内角和可知,α+2×2α=180°,5α=180°,∴α=36°,∴这个三角形的顶角为36°,故正确答案为B项.
例4 若等腰三角形的底边长是8cm,腰长是5cm,则这个等腰三角形的周长是( )
A.21cm B.18cm C.18cm或21cm D.13cm或26cm
(分析)由题意可知,8+5+5=18(cm),故正确答案为B项.
学生做一做 等腰三角形一边长为8,另一边长为4,则它的周长为 .
老师评一评 题中给出等腰三角形的两边长分别是8和4,但并没有给出哪一个是腰,哪一个是底,要分两种情况:
①若腰是8,底是4,则另一腰是8,有4+8>8,满足三角形三边关系,∴8×2+4=20;
②若腰是4,底是8,则另一腰是4,有4+4=8,不满足三角形三边关系,∴这种情况不存在.
∴这个三角形的周长为20.
小结 已知等腰三角形两边,求第三边或周长时,要全面考虑第三边的情况,求出第三边要满足三角形的三边关系,所以上题可以这样考虑:
设这个等腰三角形的第三边为x,由三角形三边关系可知,
8-4<x<8+4,
即4<x<12,
又因为这个三角形是等腰三角形,所以第三边只能考虑4或8,
由4<x<12,∴x=8,
∴这个三角形的第三边为8,其周长为8×2+4=20.
例5 如果等腰三角形的三边长均为整数,且它的周长为10cm,那么它的三边长分别为.
.
(分析)设这个三角形的腰长为xcm,则底边长为10-2x=2(5-x)cm.
共有4种情况:①当x=1cm时,10-2x=8(cm);
②当x=2cm时,10-2x=6(cm);
③当x=3cm时,10-2x=4(cm);
④当x=4cm时,10-2x=2(cm).
又由三角形三边关系可知,①②不满足三角形三边关系.
∴这个三角形的三边有两种;
3cm,3cm,4cm或4cm,4cm,2cm.
答案:3cm,3cm,4cm或4cm,4cm,2cm
综合应用题
本节知识的综合应用主要包括:(1)等腰(边)三角形的性质和判定的综合应用;(2)与方程、不等式知识的综合应用;(3)与三角形全等的综合应用.
例6 如图14-65所示,在△ABC中,AB=AC=CD,AD=DB,求∠BAC的度数.
(分析)本题由已知条件知,图中的三个三角形都是等腰三角形,相等的角或有关系的角较多,为了明确它们之间的关系,这类题往往要设其中一个角为α,然后利用α将其余的角表示出来.
解:∵AB=AC=CD,AD=DB
∴∠1=∠2,∠B=∠3,∠B=∠C.
设∠B=α,则∠B=∠3=∠C=α,∠1=∠2=∠3+∠B=2α.
在△ABC中,∠B+∠C+∠1+∠3=180°,
即α+α+2α+α=180°,
5α=180°,α=36°.
∴∠BAC=∠3+∠1=α+2α=3α=3×36°=108°.
∴∠BAC的度数为108°.
学生做一做 (1)如图14-66所示,已知AB=AC,BC=CD=AD,求∠B的度数;
(1)如图14-67所示,已知BD=CD=AC,∠B=18°,求∠ACB的度数.
老师评一评 (1)(2)题中都有几个等腰三角形,有许多相等的角,可设其中某一个角,再把其余的角表示出来.
(1)∵AB=AC,BC=CD=AD,
∴∠B=∠ACB,∠2=∠B,∠1=∠A.
设∠1=∠A=α,则∠2=∠B=2a,∠3=∠B-∠1=a.
在△BCD中,∠B+∠2+∠3=180°,
∴2α+2α+α=180°,
∴5α=180°,∴α=36°,
∴∠B=2α=2×36°=72°.
(2)∵BD=CD=AC,
∴∠1=∠B,∠2=∠A.
又∵∠2=∠1+∠B=2∠B,∠B=18°,
∴∠2=2×18°=36°.∴∠A=36°.
∴∠ACB=180°-∠A-∠B=180°-36°-18°=126°.
例7 如图14-68所示,在△ABC中,AB=AC,AD⊥BC于点D,E是AD延长线上一点,连接BE,CE.求证BE=CE.
(分析)本题主要考查等腰三角形的性质和三角形全等的判定.
证明:∵AB=AC,∴∠ABC=∠ACB.
又∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在Rt△ABD和Rt△ACD中,
∴Rt△ABD≌Rt△ACD(HL).
∴∠BAD=∠CAD(全等三角形的对应角相等).
在△ABE和△ACE中,
∴△ABE≌△ACE(SAS).
∴BE=CE(全等三角形的对应边相等).
例8 如图14-69所示,在△ABC中,AB=AC,AE是∠BAC外角∠DAC的平分线.试判断AF与BC的位置关系.
(分析)主要考查等腰三角形性质的应用.
解:AE与BC的位置关系是AE∥BC.理由如下:
∵AB=AC,∴∠B=∠C.
又∵∠DAC=∠B+∠C=2∠C,AE是∠DAC的平分线;
∴2∠EAC=∠DAC,
∴∠C=∠EAC,
∴AE∥BC(内错角相等,两直线平行).
学生做一做 (1)如图14-69所示,在△ABC中,AB=AC,AE∥BC.求证AE是△BAC的外角∠DAC的平分线;
(2)如图14-69所示,在△ABC中,AE是∠BAC的外角∠DAC的平分线,且AE∥BC.试判断△ABC的形状.
老师评一评 本题意在考查如果把已知问题中的条件与结论互换,看得到的新命题是否成立,有利于培养学生灵活分析问题和解决问题的能力.
(1)∵AB=AC,∴∠B=∠C.
又∵AE∥BC,∴∠EAC=∠C(两直线平行,内错角相等),
∠DAE=∠B(两直线平行,同位角相等).
∴∠EAC=∠DAE.
∴AE是∠DAC的平分线.
(2)△ABC是等腰三角形.理由如下:
∵AE是∠DAC的平分线,
∴∠DAE=∠EAC.
又∵AE∥BC,
∴∠DAE=∠B,∠EAC=∠C,
∴∠B=∠C,
∴AB=AC(等角对等边).
∴△ABC是等腰三角形.
例9 如图14-70所示,△ABD和△ACE是等边三角形.求证BE=CD.
(分析)欲证BE=CD,只需证明△ADC≌△ABE即可.
证明:∵△ABD和△ACE是等边三角形,
∴∠DAB=∠EAC=60°,
AD=AB,AC=AE
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠BAE.
在△DAC和△BAE中,
∴△DAC≌△BAE(SAS).
∴DC=BE(全等三角形的对应边相等).
学生做一做 如图14-71所示,B,C,D三点在一条直线上,△ABC和△ECD是等边三角形.求证BE=AD.
老师评一评 欲证BE=AD,只需证明△BCE≌△ACD即可.
∵△ABC和△ECD是等边三角形,
∴∠ACB=∠ECD=60°,BC=AC,EC=CD.
∴∠ACB+∠ACE=∠ECD+∠ACE,
即∠BCE=∠ACD.
在△BCE和△ACD中,
∴△BCE≌△ACD(SAS).
∴BE=AD(全等三角形的对应边相等).
小结 在完成类似的几何问题时,要注意灵活,举一反三,这样就可以避免题海战术,能够以点代面,同一类问题研究透彻,类似问题便能迎刃而解.
例10 等腰三角形ABC的周长为10cm,底边BC长为ycm,腰AB长为xcm.
(1)写出y关于x的函数关系式;
(2)求x的取值范围;
(3)求y的取值范围.
(分析)本题主要考查代数与几何知识的综合应用,解题时注意相关的几何知识.
解:(1)y=10-2x.
(2)∵x,y为线段,∴x>0,y>0.
∴10-2x>0,∴O<x<5.①
又∵x,y为三角形边长,
∴x+x>y,即2x>10-2x.②
由①②可得2.5<x<5.
∴x的取值范围是2.5<x<5.
(3)∵2.5<x<5,∴5<2x<10,∴-10<-2x<-5,∴O<10-2x<5,
∴O<y<5.
∴y的取值范围是O<y<5.
例11 如图14-72所示,在△ABC中.AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.
图14-72
解:∵AB=AC,∴∠ABC=∠C.
又∵∠A+∠ABC+∠C=180°,
∴∠C=(180°-∠A)=90°-∠A.
又∵BD⊥AC.∴∠BDC=90°.
∴∠DBC=90°-∠C=90°-(90°-∠A)=∠A,
∴∠DBC=∠A.
即等腰三角形腰上的高与底边的夹角等于该等腰三角形顶角的一半.
学生做一做 (1)在△ABC中,AB=AC,BD⊥AC,垂足为D,若∠DBC=25°,则∠A= ;
(2)在△ABC中,AB=AC,若∠B=70°,BD⊥AC,垂足为D,则∠DBC= .
老师评一评 由例11的结论得出;(1)题中,∠DBC=25°=∠A,∴∠A=50°.(2)题中,∵AB=AC,∴∠B=∠C=70°.∴∠A=40°.∴∠DBC=20°.
例12 如图14-73所示,在△ABC中,∠C=90°,∠BAC=60°,AB的垂直平分线交AB于D,交BC于E,若CE=3cm,求BE的长.
(分析)主要应用线段垂直平分线的性质和30°角的直角三角形的性质.
解:连接AE,
∵∠C=90°,∠BAC=60°,
∴∠B=30°.
又∵DE是AB的垂直平分线,
∴EA=EB.∴∠EAB=∠B=30°.
∴∠CAE=30°.
∴AE是∠CAB的平分线.
又∵∠C=90°,ED⊥AB,
∴DE=EC=3cm.
在Rt△DBE中,∠B=30°,∠EDB=90°,
∴DE=BE,∴BE=2×3=6(cm).
学生做一做 如图14-74所示,在Rt△ABC中,∠C=90°,∠B=15°,AB的垂直平分线分别与BC,AB交于M,N.求证MB=2AC.
老师评一评 连接MA,
∴∠C=90°,∠B=15°,
∴∠CAB=75°.
又∵MN是AB的垂直平分线,
∴MA=MB.
∴∠MAB=∠B=15°.
∴∠CAM=∠CAB-∠MAB=75°-15°=60°.
∴∠CMA=30°.
在Rt△CMA中,∠C=90°,∠CMA=30°,
∴CA=MA.∴CA=MB.
即MB=2AC.
小结 在直角三角形中证明线段的一半或2倍关系时,经常考虑30°角所对的直角边.
探索与创新题
主要考查:(1)利用等腰三角形知识探索和创新的能力;(2)图形分割;(3)辅助线的灵活应用;(4)探讨结论性问题等。
例13 如图14-75所示,已知点O是∠ABC,∠ACB的平分线的交点,且OD∥AB,OE∥AC.
(1)图形中共有哪几个等腰三角形?选一者证明之;
(2)试说明△ODE的周长与BC的关系;
(3)若BC=12cm,则△ODE的周长 .
(分析)本题(1)问主要是等腰三角形的判定;(2)问是探讨两者间的数量关系,由(1)可得;(3)问由(2)问的结果得出.
解:(1)图形中共有两个等腰三角形,它们分别是△OBD和△OCE.
以△OBD为例.
∵BO平分∠ABC,∴∠1=∠2.
又∵OD∥AB,∴∠1=∠3.
∴∠2=∠3.∴DB=OD.
∴△OBD是等腰三角形.
(2)由(1)可知,DB=DO.同理EO=EC.
∴△ODE的周长=OD+DE+EO=DB+DE+EC=BC.
∴△ODE的周长与BC的关系是:△ODE的周长=BC.
(3)由(2)可知,△ODE的周长=BC.
又∵BC=12cm,
∴△ODE的周长=12cm.
学生做一做 如图14-76所示,在△ABC中,BO,CO分别为∠ABC,∠ACB的平分线,经过点O的直线DE∥BC,交AB于点D,交AC于点E.
(1)图中等腰三角形分别是 ;
(2)DE与BD+EC的关系是:BD= .
老师评一评 欲证等腰三角形,需证角相等.
(1)∵DE∥BC,∴∠DOB=∠OBC.
又∵BO平分∠ABC,∴∠ABO=∠OBC.
∴∠DOB=∠ABO.∴DB=DO.
∴△DBO是等腰三角形.
同理EO=EC.
∴△EOC是等腰三角形.
(2)DE=DO+OE=BD+EC,
∴DE=BD+EC.
例14 如图14-77所示,在△ABC中,∠ACB=90°,BD=BC,AE=AC.试问:∠DCE是否与∠A有关?如果无关,求∠DCE的大小.
解:∠DCE与∠A无关,∠DCE=45°.理由如下:
∵BD=BC,∴∠BDC=∠BCD.
∴∠BDC=(180°-∠B)=90°-∠B.
又∵AE=AC,∴∠AEC=∠ACE.
∴∠AEC=(180°-∠A)=90°-∠A.
∴∠AEC+∠BDC=(90°-∠A)+(90°-∠B)
=180°-(∠A+∠B).
又∵∠ACB=90°,
∴∠BDC+∠AEC=180°-×90°=135°.
∴∠BDC+∠AEC=135°.
∴∠DCE=45°.
例15 如图14-78所示,在△ABC中,AD⊥BC于D,∠B=2∠C.求证AB+BD=CD.
(分析)如何利用条件∠B=2∠C,又如何得到AB+BD,不同的思考方向,会找到不同的解题方法.
证明:在CD上截取DE=DB,连接AE,
∵AD⊥BC,∴AE=AB.
∴∠B=∠AEB.
又∵∠AEB=∠C+∠CAE=2∠C,
∴∠CAE=∠C.∴AE=EC.
∴AB+BD=AE+BD=EC+ED=CD.
∴AB+BD=CD.
例16 (2003·杭州)如图14-79所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若OC=4,则PD等于( )
A.4 B.3 C.2 D.1
(分析)本题中有角平分线、平行线,这是等腰三角形的重要形成条件,另外,PD⊥OA于D,显然需要作另外一个垂直,这是角平分线性质的一个重要应用.
如图14-80所示,
过点P作PE⊥OB于E.
又∵OP平分∠BOA,PD⊥OA于D.
∴PD=PE.
∵PC∥OA,∴∠2=∠3.
又∵∠1=∠2,∠1=15°,
∴∠3=15°,CO=CP.
∴∠4=∠1+∠3=2∠1=15°×2=30°.
在Rt△CPE中,∠4=30°,∠CEP=90°,
∴PE=PC=OC=×4=2.
∴PD=2,故正确答案为C项.
学生做一做 如图14-81所示,已知矩形ABCD,沿对角线AC把△DAC翻折,AD′与BC相交于点E.判断△AEC的形状.
老师评一评 △AEC是等腰三角形,关键是证明∠EAC=∠ECA.
理由如下:
由题意可知,△ADC≌△AD′C,
∴∠DAC=∠D′AC.
又∵AD∥BC,∴∠DAC=∠ACE.
∴∠D′AC=∠ACE.∴EA=EC.
∴△EAC是等腰三角形.
小结 (1)证明线段相等是最基本的几何问题,目前常用证法有:
①若两条线段属于两个三角形,则考虑对应的三角形全等;
②若两条线段是同一个三角形两边,则考虑用等角对等边证明;
③寻找中间线段,通过等量代换来证明.
(2)类似地,我们可以对证明角相等,等边三角形的判定作归纳总结.
在证明等腰三角形时,常需应用作辅助线构造全等三角形,进而应用等腰三角形的性质为题目服务,常用的构造方法有:
①“角平分线+平行线”构造等腰三角形;
②“角平分线+垂线”构造等腰三角形;
③用“垂直平分线”构造等腰三角形;
④用“三角形中角的2倍关系”构造等腰三角形.
中考展望 点击中考
中考命题总结与展望
这部分内容在中考中多以填空、选择的形式出现,在综合题中,等腰三角形的性质和判定的知识较为常见。
中考试题预测
例1 (2004·黄冈)如图14-82所示,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证BF=2CF.
(分析)证线段2倍关系,通常考虑在直角三角形中是否有30°角.
证明:如图14-83所示,连接AF,
∵AB=AC,∠BAC=120°,
∴∠B=∠C==30°.
又∵EF是AC的垂直平分线,
∴FA=FC.∴∠C=∠FAC=30°,
∴∠BAF=∠BAC-∠FAC=120°-30°=90°.
在Rt△BAF中,∠BAF=90°,∠B=30°,
∴AF=BF.∴CF=BF.
∴BF=2CF.
例2 (2004·四川)如图14-84所示,D是△ABC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且BF=CE.求证:
(1)△ABC是等腰三角形;
(2)当∠A=90°时,试判断四边形AFDE是什么形状的四边形.
(分析)(1)只需证△BFD≌△CED,证∠B=∠C即可.
(2)只需证邻边相等,因为邻边相等的长方形是正方形.
证明:(1)∵DF⊥AB,DE⊥AC,
∴∠BFD=∠CED=90°.
又∵D是BC的中点,∴BD=CD.
在Rt△BFD和Rt△CED中,
∴Rt△BFD≌Rt△CED(HL).
∴∠B=∠C(全等三角形的对应角相等).
∴AB=AC(等角对等边).
∴△ABC是等腰三角形.
解:(2)当∠A=90°时,四边形AFDE是正方形.
理由如下:
∵∠AFD=∠AED=∠A=90°,
∴四边形AFDE是长方形.
由(1)知△BFD≌△CED,∴FD=ED.
∴四边形AFDE是正方形.
例3 (2004·陕西)如图14-85所示,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高,且CD,BE交于一点P,若∠A=50°,则∠BPC的度数是( )
A.150° B.130° C.120° D.100°
(分析)本题主要考查:(1)直角三角形两锐角互余;(2)三角形内角和是180°.具体过程如下:
∵BE⊥AC,CD⊥AB,
∴∠AEB=∠ADC=90°.
又∵∠A=50°,
∴∠ABE=∠ACD=90°-50°=40°.
又∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°.
∴∠PBC+∠PCB=(∠ABC+∠ACB)-(∠ABE+∠ACD)
=130°-(40°+40°)=50°.
∴∠BPC=180°-(∠PBC+∠PCB)=180°-50°=130°.
∴∠BPC=130°.故正确答案为B项.
例4 (中考预测题)如图14-86所示,在梯形ABCD中,AB=AD,AD∥BC,∠A=100°,试求∠DBC的度数.
(分析)本题要求一个角的度数,已知条件中的AD∥BC恰与角有密切联系,所以应该充分利用.
解:由AD=AB知,∠ADB=∠ABD(等腰三角形的底角相等),由AD∥BC知,∠ADB=∠DBC(两直线平行,内错角相等).
可见∠ABD=∠DBC.
而∠A+∠ABC=180°(两直线平行,同旁内角互补),
∠A=100°,所以100°+2∠DBC=180°.
可以得出∠DBC=40°.
例5 (2004·青海)如图14-87所示,把一张平行四边形纸片ABCD沿BD对折,使C点落在E处,BE与AD相交于点O,若∠DBC=15°,则∠BOD= .
(分析)由题意可知△BDC≌△BDE.
∴∠DBC=∠DBE.
又∵AD∥BC,∴∠ODB=∠DBC.
∴∠OBD=∠ODB.
又∵∠DBC=15°,
∴∠OBD=∠ODB=15°.
∴∠BOD=180°-15°×2=150°.
课堂小结 本节归纳
本节主要学习了:
(1)等腰三角形的概念、性质和判定;
(2)等边三角形的概念、性质和判定;
(3)直角三角形(有一个角是30°的直角三角形)的性质.
习题选解 课本习题
课本第149~151页
习题14.3
1.(1)35°,35°(2)80°,20°或50°,50°
2.证明:∵AD∥BC,∴∠ADB=∠DBC.
又∵BD平分∠ABC,∴∠ABD=∠DBC.
∴∠ADB=∠ABD,∴AB=AD(等角对等边).
3.解:∵五角星的五个角都是顶角为36°的等腰三角形,
∴每个底角的度数是(180°-36°)=72°.
∴∠AMB=180°-72°=108°.
4.解:∵AB=AC,∠BAC=100°,
∴∠B=∠C=×(180°-100°)=40°.
又∵AD⊥BC,∴AD是∠BAC的平分线,
∴∠BAD=∠CAD=×100°=50°.
5.解:△ECB是等腰三角形.理由如下:
∵CE∥AD,∴∠A=∠CEB.
又∵∠A=∠B,∴∠CEB=∠B.∴CE=CB.
∴△CBE是等腰三角形.
6.证明:∵AB=AC,∴∠B=∠C.
又∵AD=AE,∴∠ADE=∠AED.
∴∠ADB=∠AEC.
在△ABD和△ACE中,
∴△ABD≌△ACE(AAS)
∴BD=CE(全等三角形的对应边相等).
7.解:∵AB=AC,∠A=40°,
∴∠ABC=∠C=×(180°-40°)=70°.
又∵MN是AB的垂直平分线,∴DA=DB.
∴∠A=∠DBA=40°.
∴∠DBC=∠ABC-∠ABD=70°-40°=30°.
9.解:∵∠PAB=∠PBA,∴PA=PB.这是利用了等腰三角形的判定
10.解:∵∠NBC=84°,∠NAC=42°,∠NBC=∠NAC+∠C,
84°=42°+∠C,∴∠C=42°.∴BC=BA.
又∵BA=15×(10-8)=30(海里),
∴BC=30海里.
即从海岛B到灯塔C的距离是30海里.
11.证明:∵△ABD,△AEC都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠EAC=60°.
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠BAE.
在△ADC和△ABE中,
∴△ADC≌△ABE(SAS).
∴DC=BE.
12.解:等腰三角形两底角的平分线相等,等腰三角形两腰上的中线相等,等腰三角形两腰上的高相等.以等腰三角形两腰上的高相等为例证明.
已知:如图14-88所示,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D,E.
求证:BD=CE.
证明:∵AB=AC,∴∠ABC=∠ACB.
又∵BD⊥AC,CE⊥AB,∴∠BEC=∠CDB=90°.
在Rt△BCE和Rt△CBD中,
∴Rt△BCE≌Rt△CBD(AAS).
∴BD=CE(全等三角形的对应边相等).
13.提示:(1)∠ECD=∠EDC;(2)OC=OD;(3)OE是CD的垂直平分线.
理由如下:
∵OE平分∠AOB,ED⊥OB,EC⊥OA,垂足分别为D,C,
∴ED=EC.∴∠EDC=∠ECD.
在Rt△ODE和Rt△OCE中,
∴Rt△ODE≌Rt△OCE(HL).
∴OD=OC.∴△ODC是等腰三角形.
又∵OE是∠DOC的平分线,
∴OE是底边CD上的高和中线.
即OE是线段DC的垂直平分线.
14.解:如图14-89所示.
作法如下:作∠CAB的平分线AD,交于BC于点D,再作DE上AB,垂足为E.
∵∠C=90°,∠B=30°,
∴∠CAB=60°.∴∠1=∠2=30°.
又∵DE⊥AB,∠C=90°,∴∠C=∠AED=90°.
在Rt△ACD和Rt△AED中,
∴Rt△ACD≌Rt△AED(AAS).
又∵∠2=∠B=30°,∴DA=DB.
又∵DE⊥AB,∴∠AED=∠BED=90°.
在Rt△ADE和Rt△BDE中,
∴Rt△ADE≌Rt△BDE(AAS).
∴Rt△ADC≌Rt△ADE≌Rt△BDE.
自我评价 知识巩固
1.等边三角形的两条中线所成的钝角的度数是( )
A.120° B.130° C.150° D.160°
2.设等腰三角形的顶角为∠A,则∠A的取值范围是( )
A.0°≤∠A<180° B.0°<∠A<180°
C.0°≤∠A<180° D.0°<∠A<90°
3.一个三角形的外角分别是135°,90°,135°,则这个三角形是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
4.如果等腰三角形一底角为α,那么( )
A.α≤45° B.0°<α<90° C.α≤90° D.90°<α<180°
5.等腰三角形一腰上的高与底边所成的角等于( )
A.顶角 B.顶角的一半 C.顶角的2倍 D.底角的一半
6.如图14-90所示,在△ABC中,AB=AC,BD,CE是角平分线,图中的等腰三角形共有( )
A.6个 B.5个 C.4个 D.3个
7.如图14-91所示,在△ABC中,BO平分∠ABC,CO平分∠ACB,MN∥BC,MN经过点O,若AB=12,AC=18,则△AMN的周长是( )
A.15 B.18 C.24 D.30
8.如图14-92所示,O是∠ABC,∠ACB的平分线的交点,OD∥AB,交BC于D,OE∥AC交BC于E,若BC=10cm,则面DOE的周长为( )
A.8cm B.9cm C.10cm D.11cm
9.在△ABC中,若AB=AC,∠A=90°,则∠B= ,∠C= .
10.如果一个三角形的两个内角分别为70°,40°,那么这个三角形是 .
11.在△ABC中,AB=AC,∠A=60°,则∠B= ,∠C= ,△ABC是 三角形.
12.已知等腰三角形的一个底角等于顶角的2倍,这个等腰三角形各角的度数分别是 .
13.如图14-93所示,BD是△ABC的角平分线,∠A=36°,∠C=72°,则图中共有 个等腰三角形,它们分别是 .
14.(1)如果等腰三角形的两边长分别是4cm,7cm,那么它的周长是 ;
(2)如果等腰三角形的两边长分别是5cm和10cm,则这个等腰三角形的周长是 .
15.等腰三角形两腰上的高、中线,两底角平分线分别 .
16.在等腰三角形中,如果顶角是一个底角的2倍,那么这个三角形是 三角形.
17.若三角形是轴对称图形,且有一个角是60°,则这个三角形是 三角形.
18.一个等腰三角形的周长为18cm,一边长为4cm,求其他两边的长.
19.如图14-94所示,在△ABC中,AB=AC,DE∥BC,交AB于D,交AC于E,求证△ADE也是等腰三角形.
20.如图14-95所示,四边形ABCD中,AD∥BC,AB=AD,试证明BD是∠ABC的平分线.
21.如图14-96所示,∠1=∠2,BD=CD,试证明△ABC是等腰三角形.
22.在△ABC中,AB=AC,CD为底边上的高,△ABC的周长为16cm,△ABD的周长为12cm,求AD的长.
23.如图14-97所示,CE是△ABC的角平分线,过点E画BC的平行线,交AC于点D,交外角∠ACG的平分线于点F.试证明DE=DF.
24.(1)如图14-98所示,∠BAC=90°,AD⊥BC,垂足为D,BE平分∠ABC,交AC于E,交AD于F.试判断△AEF的形状,并说明理由;
(2)如图14-98所示,已知∠BAC=90°,AD⊥BC,垂足为D,AE=AF.试说明BE平分∠ABC.
参考答案
1.A 2.B 3.D 4.B 5.B 6.A 7.D 8.C 9.45°,45° 10.等腰三角形
11.60° 60° 等边 12.36°,72°,72° 13.3 △ABC,△ ABD,△BCD
14.(1)15cm或18cm (2)25cm 15.相等 16.等腰直角 17.等边
18.提示:分两种情况讨论:
①若以4cm为底边长,设腰长为xcm,
则有4+2x=18,∴x=7.
∴另外两边的长为7cm,7cm.
②若以4cm为腰长,设底边长为ycm,则有
4×2+y=18,∴y=10.
∴4+4<10,不满足三角形的三边关系,
∴4cm,4cm,10cm不能组成三角形.
∴三角形的另外两条边长为7cm,7cm.
19.证明:∵AB=AC,∴∠B=∠C.
又∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.
∴∠ADE=∠AED.∴AD=AE.
∴△ADE是等腰三角形.
20.证明:∵AD∥BC,∴∠ADB=∠DBC.
又∵AB=AD,∴∠ABD=∠ADB.
∴∠DBC=∠ABD.
∴BD是∠ABC的平分线.
21.证明:∵BD=DC,∴∠DBC=∠DCB.
又∵∠1=∠2,
∴∠DBC+∠1=∠DCB+∠2,
即∠ABC=∠ACB.∴AB=AC.
∴△ABC是等腰三角形.
22.解:如图14-99所示.
∵AB=AC,AD为BC边上的高,
∴BD=DC.
又∵△ABD的周长为12cm,△ABC的周长为16cm,
∴AB+BD=16÷2=8(cm).
AB+BD+AD=12(cm).
∴AD=12-8=4(cm).
23.证明:∵CE是∠ACB的平分线,∴∠ACE=∠ECB.
又∵EF∥BC,∴∠DEC=∠ECB.
∴∠ACE=∠DEC.∴DE=DC.
同理DF=DC.∴DE=DF.
24.解:(1)如图14-100所示.
∵BE平分∠ABC,∴∠1=∠2.
又∵∠BAC=90°,AD⊥BC,
∴∠3=90°-∠1,∠4=90°-∠2,∴∠3=∠4.
又∵∠4=∠5,∴∠3=∠5,∴AE=AF.
∴△AEF是等腰三角形.
(2)如图14-101所示.
∵AE=AF,∴∠1=∠2.
又∵∠1=∠3,∴∠2=∠3.
又∵∠BAC=90°,AD⊥BC,
∴∠4=90°-∠2,∠5=90°-∠3,∴∠4=∠5.
∴BE是∠ABC的平分线.
