等腰三角形的性质2[上学期]
文档属性
| 名称 | 等腰三角形的性质2[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-10 00:00:00 | ||
图片预览




文档简介
课件11张PPT。等腰三角形的性质复习提问1、等腰三角形的性质?2、等腰三角形的性质的两个推论?1.等腰三角形 、 、 、
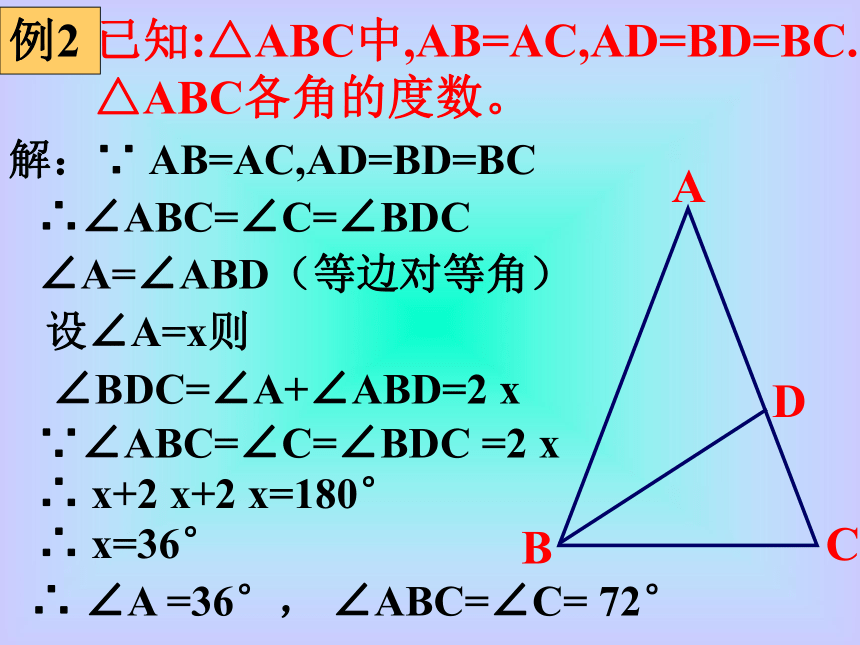
互相重合。顶角平分线底边中线底边高填空:45°30°45°和45°题 型 探 究例2已知:△ABC中,AB=AC,AD=BD=BC.求: △ABC各角的度数。解:∵ AB=AC,AD=BD=BC∴∠ABC=∠C=∠BDC∠A=∠ABD(等边对等角)设∠A=x则∠BDC=∠A+∠ABD=2 x∵∠ABC=∠C=∠BDC =2 x∴ x+2 x+2 x=180°∴ x=36°∴ ∠A =36°, ∠ABC=∠C= 72°变式1ABCD已知:△ABC中,AB=AC, AD=ED=EC.CD=BD求△ABC各角的度数。E变式2ABCD已知:如图,AB=BC=CD=ED=EF.EFMN∠A=15°,你能求出哪些角的度数?例3已知:点D、E在△ABC中, AB=AC,AD=AE. 求证:BD=CE。ABCDE练习:1.△ABC是等边三角形,中线BD、CE相交于点O,则以点O为顶点的4个角的度数是2.已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC。 求证:AO⊥BCC小结1.等腰三角形的性质及其的应用。2.培养方程的思想。3.利用“三线合一”的一般辅助线。
互相重合。顶角平分线底边中线底边高填空:45°30°45°和45°题 型 探 究例2已知:△ABC中,AB=AC,AD=BD=BC.求: △ABC各角的度数。解:∵ AB=AC,AD=BD=BC∴∠ABC=∠C=∠BDC∠A=∠ABD(等边对等角)设∠A=x则∠BDC=∠A+∠ABD=2 x∵∠ABC=∠C=∠BDC =2 x∴ x+2 x+2 x=180°∴ x=36°∴ ∠A =36°, ∠ABC=∠C= 72°变式1ABCD已知:△ABC中,AB=AC, AD=ED=EC.CD=BD求△ABC各角的度数。E变式2ABCD已知:如图,AB=BC=CD=ED=EF.EFMN∠A=15°,你能求出哪些角的度数?例3已知:点D、E在△ABC中, AB=AC,AD=AE. 求证:BD=CE。ABCDE练习:1.△ABC是等边三角形,中线BD、CE相交于点O,则以点O为顶点的4个角的度数是2.已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC。 求证:AO⊥BCC小结1.等腰三角形的性质及其的应用。2.培养方程的思想。3.利用“三线合一”的一般辅助线。
