数学人教A版(2019)必修第一册3.3幂函数(共32张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.3幂函数(共32张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 17:11:51 | ||
图片预览










文档简介
(共32张PPT)
人教A版2019 必修第一册
第三章 函数的概念与性质
3. 3 幂函数
幂函数的概念
【探究】(1)如果卢老师以1元/kg的价格购买了某种蔬菜t千克,那么他需要支付
的钱数P=t元,这里P是t的函数;
(2)如果正方形的边长为a,那么正方形的面积S=a2,这里S是a的函数;
(3)如果立方体的棱长为b,那么立方体的体积V=b3,这里V是b的函数;
(4)如果正方形广场的面积为S,那么广场的边长c= ,这里c是S的函数;
(5)如果某人t秒内汽车前进了1km,那么他的平均速度v= km/s,这里
v是t的函数;
【以下各个函数有什么共同的特征?】
可以发现,这些函数的表达式都具有幂的形式,而且都是以幂的底数为自变量,
幂的指数都是常数.分别是1,2,3,0.5,-1;它们都是形如 的函数.
一般地,函数 叫做幂函数,其中 是自变量, 是常数.
【1】在函数① ② ③ ④
⑤ ⑥ 中,是幂函数的是( ) .
【解】根据幂函数的定义,只有①⑤⑥是幂函数.
选项②系数不为1;选项③系数不为1且多了常数项
选项④同理.
①⑤⑥
幂函数的特征
【1】 的系数为1
【2】 的底数为自变量
【3】 的指数为常数
只有同时满足这三个条件的,才是幂函数.形如
等的函数不是幂函数.
判断一个函数是不是幂函数的依据是该函数是否为
( 为常数)的形式.反过来,若一个函数为幂函数,那么它也一定具有这个形式.在我们解决某些问题的时候这个结论有奇效.
【1】已知幂函数 的图像经过点 ,求这个函数的表达式.
【解】由题意设函数的表达式为
把点 代入,得:
即 ,所以
所以这个函数的表达式为
和初中解决一次函数一样,利用待定系数法.因为幂函数只有一个系数,所以只需要一个点的坐标就可以求写出幂函数的表达式.
幂函数的图像
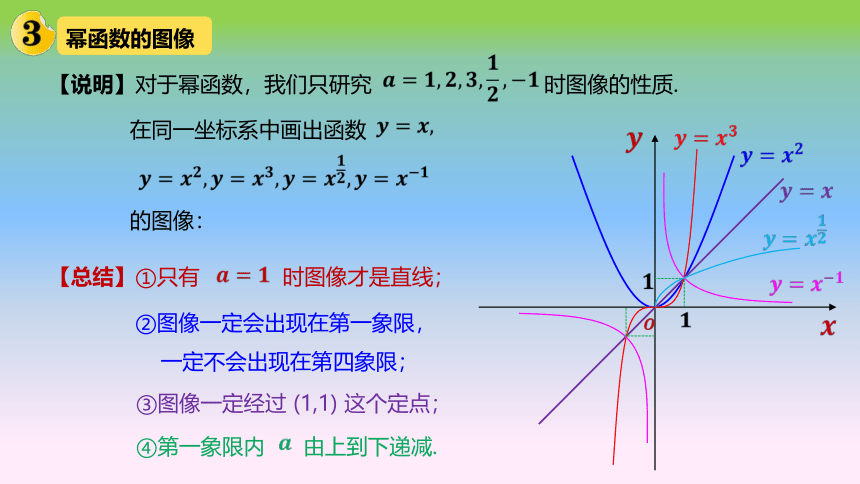
【说明】对于幂函数,我们只研究 时图像的性质.
在同一坐标系中画出函数
的图像:
【总结】①只有 时图像才是直线;
②图像一定会出现在第一象限,
一定不会出现在第四象限;
③图像一定经过 (1,1) 这个定点;
④第一象限内 由上到下递减.
幂函数的图像
【说明】对于幂函数,我们只研究 时图像的性质.
在同一坐标系中画出函数
的图像:
【总结】⑤ 时,图像在定义域内上升;
⑥ 时,图像在第一象限下降;
⑦只有 时,图像才与坐标轴
相交,且交点一定为原点;
⑧ 时,图像是y=1这条直线,除去一个点.
幂函数的性质:
(1)过定点(1,1);
(2)幂函数的图象一定会在第一象限,一定不在第四象限;
(3)当时,函数在区间上是增函数;
(4)当时,函数在区间上是减函数;
(5)在上,指数越大,幂函数图象越靠近轴(指大图低);
(6)在上,指数越大,幂函数图象越远离轴(指大图高);
幂函数的性质
奇函数
奇函数
奇函数
偶函数
非奇非偶函数
增函数
增函数
增函数
【1】求幂函数 的定义域并讨论其奇偶性和单调性.
【解】因为 , ,又 为
两个连续的正整数相乘,其结果必为正偶数,所以
为正奇数,所以函数的定义域为R.
由 为正奇数,得
,所以 为增函数.
因为 ,所以 是正的奇次方根,所以
在定义域内为增函数.
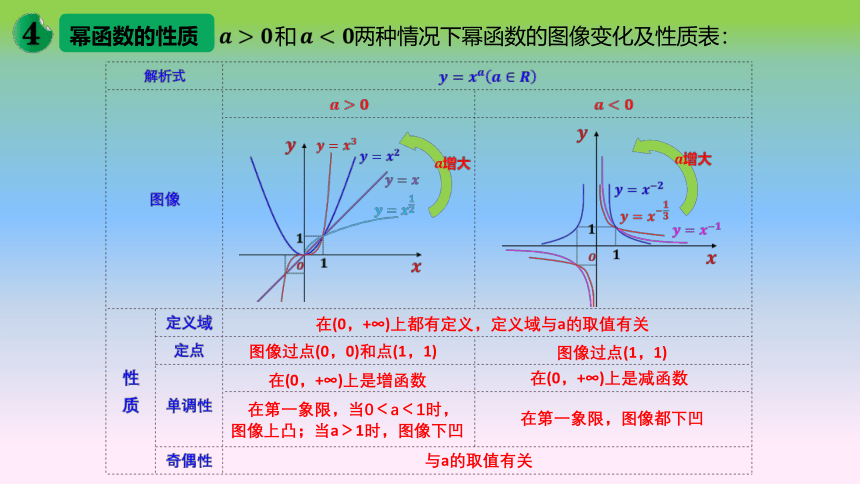
幂函数的性质
和 两种情况下幂函数的图像变化及性质表:
在(0,+∞)上都有定义,定义域与a的取值有关
图像过点(0,0)和点(1,1)
图像过点(1,1)
在(0,+∞)上是增函数
在(0,+∞)上是减函数
在第一象限,当0<a<1时,
图像上凸;当a>1时,图像下凹
在第一象限,图像都下凹
与a的取值有关
【2】利用幂函数的性质,比较下列两个数的大小.
【解】设 ,则 在R上为增函数.
比较大小用作差法.由增减性,根据自变量的大小,比较函数值的大小;或者根据函数值的大小,比较自变量的大小.
∵ -1.5<-1.4,∴ (-1.5)3<(-1.4)3
(-1.5)3 和 (-1.4)3
幂函数 奇偶性的判断方法
奇函数
偶函数
奇函数
偶函数
非奇非偶函数
证明幂函数的增减性
【例题】证明幂函数 是增函数.
【证明】函数的定义域是[0,+∞).
因为 , ,所以
即幂函数 是增函数.
题①
已知幂函数的图像经过点(9,3),求这个幂函数的解析式.
设幂函数为 ,
因为图像经过点(9,3),
所以 ,
所以 .
所以 ,
变1.已知幂函数在上为减函数,则等于().
解:∵为幂函数
∴=1,
又∵幂函数在上为减函数
∴.即
∴=
题型二:幂函数的图象及应用
若点在幂函数的图象上,点在幂函数的图象上,问当为何值时,(1)
解:∵设,则
∴=2.即
同理可得,
画出和的函数图象,
则由图象可知:当或时,;
当时,;
当时,.
题②
变2:若四个幂函数图象在同一坐标系中的图象如图所示,则的大小关系是().
答案:B.在(1,+)上,指大图高.
解决幂函数图象问题的原则:
(1)根据图象的高低判断幂指数的大小:在上,指数越大,幂函数图象越靠近轴(指大图低);在上,指数越大,幂函数图象越远离轴(指大图高).
(2)当时,幂函数的图象都经过和点.
题③
比较下面两组数的大小.
(1) 和 (2) 和
题型三:利用幂函数的单调性比较大小
变3-1.比较下列各组数中两个数的大小.
与;与;与.
解:(1)∵幂函数在上是单调递增的,
又,∴>.
(2)∵幂函数在上是单调递减的,
又,∴.
解:(3)∵幂函数在上是单调递增的,
又,∴>
又∵在上是单调递增的,
且,∴
∴
变3.比较下列各组数中两个数的大小.
与;与;与.
变3-2.比较下列各题中两个幂的值的大小.
与;与.
解:(1)∵幂函数在上是单调递减的,
又,∴
(2)∵,幂函数在上是单调递增的,
且,∴,即
比较幂的大小的3种基本方法:
直接法 当幂指数相同时,可直接利用幂函数的单调性来比较
转化法 当幂指数不同时,可以先转化为相同的幂指数,再利用单调性来比较大小
中间量法 当底数不同且幂指数也不同时,不能运用单调性比较大小,可选取适当的中间值,从而达到比较大小的目的
题④
如果幂函数的图象不过原点,求实数m的值
题5
在同一平面直角坐标系中画出函数 与 的图象,并利用图象求不等式 的解集.
题型四:幂函数性质的综合应用
例.已知函数
(1)试确定该函数的定义域,并指明该函数在定义域上的单调性;
解:(1)∵,,
∴中有一个必为偶数,
∴该函数的定义域为,
由幂函数的性质知,该函数在定义域上单调递增.
例.已知函数
(2)若该函数图象经过点,试确定的值,并求满足条件的实数的取值范围.
解:(2)∵该函数图象经过点,∴,
∴,即=2,∴
由,得解之得
故的值为1,满足条件的实数的取值范围为
.
变.已知幂函数为偶函数.
(1)求的值;
(2)若,求实数的值.
解:(1)∵幂函数为偶函数,
∴,解得(舍去)或
∴,∴ .
(2)由,可得.
即
.
解之得
练习
解决幂函数的综合问题,要注意以下几点:
(1)充分利用幂函数的图象、性质解题,如图象过定点、单调性、奇偶性等;
(2)注意运用常见的思想方法解题,如分类讨论、数形结合等.
题⑤
已知在区间上,函数与都是减函数,试求的取值范围.
人教A版2019 必修第一册
第三章 函数的概念与性质
3. 3 幂函数
幂函数的概念
【探究】(1)如果卢老师以1元/kg的价格购买了某种蔬菜t千克,那么他需要支付
的钱数P=t元,这里P是t的函数;
(2)如果正方形的边长为a,那么正方形的面积S=a2,这里S是a的函数;
(3)如果立方体的棱长为b,那么立方体的体积V=b3,这里V是b的函数;
(4)如果正方形广场的面积为S,那么广场的边长c= ,这里c是S的函数;
(5)如果某人t秒内汽车前进了1km,那么他的平均速度v= km/s,这里
v是t的函数;
【以下各个函数有什么共同的特征?】
可以发现,这些函数的表达式都具有幂的形式,而且都是以幂的底数为自变量,
幂的指数都是常数.分别是1,2,3,0.5,-1;它们都是形如 的函数.
一般地,函数 叫做幂函数,其中 是自变量, 是常数.
【1】在函数① ② ③ ④
⑤ ⑥ 中,是幂函数的是( ) .
【解】根据幂函数的定义,只有①⑤⑥是幂函数.
选项②系数不为1;选项③系数不为1且多了常数项
选项④同理.
①⑤⑥
幂函数的特征
【1】 的系数为1
【2】 的底数为自变量
【3】 的指数为常数
只有同时满足这三个条件的,才是幂函数.形如
等的函数不是幂函数.
判断一个函数是不是幂函数的依据是该函数是否为
( 为常数)的形式.反过来,若一个函数为幂函数,那么它也一定具有这个形式.在我们解决某些问题的时候这个结论有奇效.
【1】已知幂函数 的图像经过点 ,求这个函数的表达式.
【解】由题意设函数的表达式为
把点 代入,得:
即 ,所以
所以这个函数的表达式为
和初中解决一次函数一样,利用待定系数法.因为幂函数只有一个系数,所以只需要一个点的坐标就可以求写出幂函数的表达式.
幂函数的图像
【说明】对于幂函数,我们只研究 时图像的性质.
在同一坐标系中画出函数
的图像:
【总结】①只有 时图像才是直线;
②图像一定会出现在第一象限,
一定不会出现在第四象限;
③图像一定经过 (1,1) 这个定点;
④第一象限内 由上到下递减.
幂函数的图像
【说明】对于幂函数,我们只研究 时图像的性质.
在同一坐标系中画出函数
的图像:
【总结】⑤ 时,图像在定义域内上升;
⑥ 时,图像在第一象限下降;
⑦只有 时,图像才与坐标轴
相交,且交点一定为原点;
⑧ 时,图像是y=1这条直线,除去一个点.
幂函数的性质:
(1)过定点(1,1);
(2)幂函数的图象一定会在第一象限,一定不在第四象限;
(3)当时,函数在区间上是增函数;
(4)当时,函数在区间上是减函数;
(5)在上,指数越大,幂函数图象越靠近轴(指大图低);
(6)在上,指数越大,幂函数图象越远离轴(指大图高);
幂函数的性质
奇函数
奇函数
奇函数
偶函数
非奇非偶函数
增函数
增函数
增函数
【1】求幂函数 的定义域并讨论其奇偶性和单调性.
【解】因为 , ,又 为
两个连续的正整数相乘,其结果必为正偶数,所以
为正奇数,所以函数的定义域为R.
由 为正奇数,得
,所以 为增函数.
因为 ,所以 是正的奇次方根,所以
在定义域内为增函数.
幂函数的性质
和 两种情况下幂函数的图像变化及性质表:
在(0,+∞)上都有定义,定义域与a的取值有关
图像过点(0,0)和点(1,1)
图像过点(1,1)
在(0,+∞)上是增函数
在(0,+∞)上是减函数
在第一象限,当0<a<1时,
图像上凸;当a>1时,图像下凹
在第一象限,图像都下凹
与a的取值有关
【2】利用幂函数的性质,比较下列两个数的大小.
【解】设 ,则 在R上为增函数.
比较大小用作差法.由增减性,根据自变量的大小,比较函数值的大小;或者根据函数值的大小,比较自变量的大小.
∵ -1.5<-1.4,∴ (-1.5)3<(-1.4)3
(-1.5)3 和 (-1.4)3
幂函数 奇偶性的判断方法
奇函数
偶函数
奇函数
偶函数
非奇非偶函数
证明幂函数的增减性
【例题】证明幂函数 是增函数.
【证明】函数的定义域是[0,+∞).
因为 , ,所以
即幂函数 是增函数.
题①
已知幂函数的图像经过点(9,3),求这个幂函数的解析式.
设幂函数为 ,
因为图像经过点(9,3),
所以 ,
所以 .
所以 ,
变1.已知幂函数在上为减函数,则等于().
解:∵为幂函数
∴=1,
又∵幂函数在上为减函数
∴.即
∴=
题型二:幂函数的图象及应用
若点在幂函数的图象上,点在幂函数的图象上,问当为何值时,(1)
解:∵设,则
∴=2.即
同理可得,
画出和的函数图象,
则由图象可知:当或时,;
当时,;
当时,.
题②
变2:若四个幂函数图象在同一坐标系中的图象如图所示,则的大小关系是().
答案:B.在(1,+)上,指大图高.
解决幂函数图象问题的原则:
(1)根据图象的高低判断幂指数的大小:在上,指数越大,幂函数图象越靠近轴(指大图低);在上,指数越大,幂函数图象越远离轴(指大图高).
(2)当时,幂函数的图象都经过和点.
题③
比较下面两组数的大小.
(1) 和 (2) 和
题型三:利用幂函数的单调性比较大小
变3-1.比较下列各组数中两个数的大小.
与;与;与.
解:(1)∵幂函数在上是单调递增的,
又,∴>.
(2)∵幂函数在上是单调递减的,
又,∴.
解:(3)∵幂函数在上是单调递增的,
又,∴>
又∵在上是单调递增的,
且,∴
∴
变3.比较下列各组数中两个数的大小.
与;与;与.
变3-2.比较下列各题中两个幂的值的大小.
与;与.
解:(1)∵幂函数在上是单调递减的,
又,∴
(2)∵,幂函数在上是单调递增的,
且,∴,即
比较幂的大小的3种基本方法:
直接法 当幂指数相同时,可直接利用幂函数的单调性来比较
转化法 当幂指数不同时,可以先转化为相同的幂指数,再利用单调性来比较大小
中间量法 当底数不同且幂指数也不同时,不能运用单调性比较大小,可选取适当的中间值,从而达到比较大小的目的
题④
如果幂函数的图象不过原点,求实数m的值
题5
在同一平面直角坐标系中画出函数 与 的图象,并利用图象求不等式 的解集.
题型四:幂函数性质的综合应用
例.已知函数
(1)试确定该函数的定义域,并指明该函数在定义域上的单调性;
解:(1)∵,,
∴中有一个必为偶数,
∴该函数的定义域为,
由幂函数的性质知,该函数在定义域上单调递增.
例.已知函数
(2)若该函数图象经过点,试确定的值,并求满足条件的实数的取值范围.
解:(2)∵该函数图象经过点,∴,
∴,即=2,∴
由,得解之得
故的值为1,满足条件的实数的取值范围为
.
变.已知幂函数为偶函数.
(1)求的值;
(2)若,求实数的值.
解:(1)∵幂函数为偶函数,
∴,解得(舍去)或
∴,∴ .
(2)由,可得.
即
.
解之得
练习
解决幂函数的综合问题,要注意以下几点:
(1)充分利用幂函数的图象、性质解题,如图象过定点、单调性、奇偶性等;
(2)注意运用常见的思想方法解题,如分类讨论、数形结合等.
题⑤
已知在区间上,函数与都是减函数,试求的取值范围.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
