数学人教A版(2019)必修第一册3.4 函数的应用(一) (共37张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.4 函数的应用(一) (共37张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 518.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 15:45:53 | ||
图片预览










文档简介
(共37张PPT)
3.4 函数的应用(一)
学习目标
1.理解函数是描述客观世界中变量关系和规律的重要数学语言和工具.
2.在实际情境中,会选择合适的函数模型刻画现实问题的变化规律,培养数学建模、数据分析和数学运算素养.
知识梳理·自主探究
师生互动·合作探究
知识梳理·自主探究
知识探究
1.一次函数模型
形如y=kx+b(k≠0)的函数模型是一次函数模型,一次函数的图象为直线,应用一次函数的性质,可以求参数值及函数解析式等.
2.二次函数模型
(1)形如y=ax2+bx+c(a≠0)的函数模型是二次函数模型.
(2)二次函数模型是生活中最常见的一种数学模型,依据实际问题建立二次函数的解析式后,利用配方法求最值简单易懂,有时可以依据二次函数的单调性求最值,从而解决最大、最小等问题.
3.分段函数模型
(1)分段函数模型
分段函数是指函数解析式由几段组成的函数,根据自变量取值范围的不同,由题设确定出不同的函数关系式.
(2)分段函数模型的应用
①分段函数模型应用的关键是确定分段的各边界点.即明确自变量的取值区间,对每一区间进行分类讨论,从而写出函数解析式,需注意分段函数的最值,是各区间上解析式取得的最大值或最小值.
②要注意结合实际问题的实际意义,有时还可结合图象去求解.
师生互动·合作探究
探究点一
一次函数模型
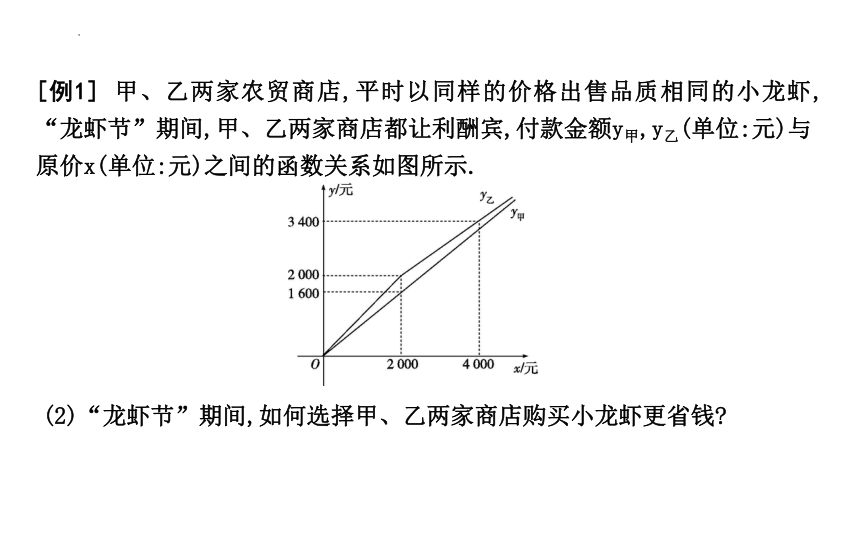
[例1] 甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾,
“龙虾节”期间,甲、乙两家商店都让利酬宾,付款金额y甲,y乙(单位:元)与原价x(单位:元)之间的函数关系如图所示.
(1)写出y甲,y乙关于x的函数关系式;
[例1] 甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾,
“龙虾节”期间,甲、乙两家商店都让利酬宾,付款金额y甲,y乙(单位:元)与原价x(单位:元)之间的函数关系如图所示.
(2)“龙虾节”期间,如何选择甲、乙两家商店购买小龙虾更省钱
解:(2)当00.7x+600,解得x>6 000;若到甲、乙两商店购买花钱一样,则0.8x=0.7x+600,解得x=6 000;故当购买金额按原价小于6 000元时,到甲商店购买更省钱;当购买金额按原价大于6 000元时,到乙商店购买更省钱;当购买金额按原价等于6 000元时,到甲、乙两商店购买花钱一样.
方法总结
建立一次函数模型,常设为y=kx+b(k≠0),然后用待定系数法求出k,b的值,再根据单调性求最值或利用方程、不等式思想解题.
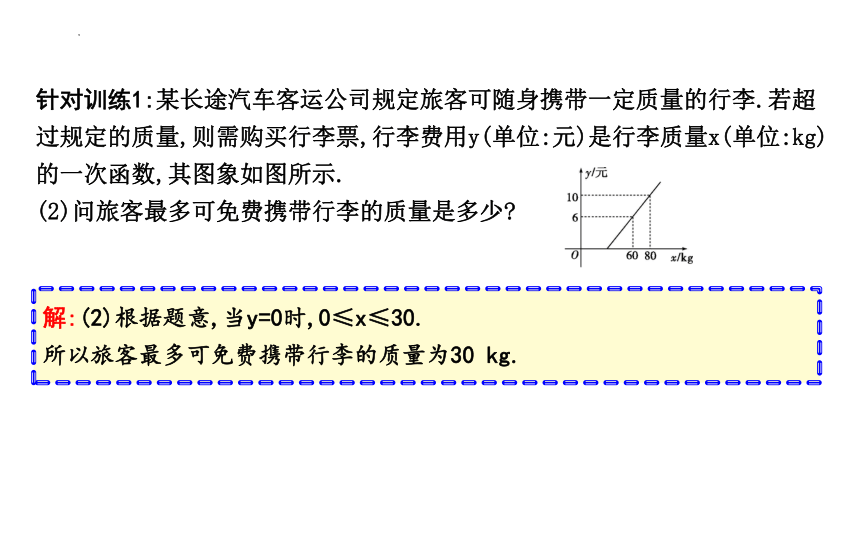
针对训练1:某长途汽车客运公司规定旅客可随身携带一定质量的行李.若超过规定的质量,则需购买行李票,行李费用y(单位:元)是行李质量x(单位:kg)的一次函数,其图象如图所示.
(1)根据图象数据,求y与x之间的函数关系式;
针对训练1:某长途汽车客运公司规定旅客可随身携带一定质量的行李.若超过规定的质量,则需购买行李票,行李费用y(单位:元)是行李质量x(单位:kg)的一次函数,其图象如图所示.
(2)问旅客最多可免费携带行李的质量是多少
解:(2)根据题意,当y=0时,0≤x≤30.
所以旅客最多可免费携带行李的质量为30 kg.
探究点二
二次函数模型
[例2] 某农家旅游公司有客房160间,每间房单价为200元时,每天都客满.已知每间房单价每提高20元,则客房出租数就会减少10间,若不考虑其他因素,旅游公司把每间房单价提到多少时,每天客房的租金总收入最高
解:设每间房单价提高x个20元时,每天客房的租金总收入为y元.
此时每间房单价为(200+20x)元,而客房出租数将减少10x间,即为(160-10x)间,因此
y=(200+20x)(160-10x)=200(10+x)(16-x)
=200(-x2+6x+160)=200[-(x-3)2+169]=-200(x-3)2+33 800.
从而可知,当x=3时,y的最大值为33 800.
因此每间房单价提到200+20×3=260元时,每天客房的租金总收入最高.
方法总结
(1)二次函数与二次方程之间有密切的关系,解题时要注意题目中的约束
条件.
(2)求解二次函数问题应注意二次函数图象的对称性与单调性.
(3)解决实际生活中用料最省、利润最大等问题时,一般建立二次函数模型,还需掌握一些常见的关系式,如利润=(商品销售单价-商品成本单价)×销售量等.
针对训练2:某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(单位:件)与销售单价x(单位:元/件)的关系可近似看作一次函数y=kx+b(如图所示).
(1)根据图象,求一次函数y=kx+b的解析式;
针对训练2:某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(单位:件)与销售单价x(单位:元/件)的关系可近似看作一次函数y=kx+b(如图所示).
(2)设公司获得的利润为S(单位:元)(利润=销售总价-成本总价,销售总价=销售单价×销售量,成本总价=成本单价×销售量).
①试用销售单价x表示利润S;
解:(2)①由(1)知,S=xy-50y=(-x+100)(x-50)
=-x2+150x-5 000(50≤x≤80).
针对训练2:某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(单位:件)与销售单价x(单位:元/件)的关系可近似看作一次函数y=kx+b(如图所示).
(2)设公司获得的利润为S(单位:元)(利润=销售总价-成本总价,销售总价=销售单价×销售量,成本总价=成本单价×销售量).
②当销售单价定为多少时,该公司可获得最大利润 最大利润是多少 此时的销售量是多少
解:②由①可知,S=-(x-75)2+625(50≤x≤80),
其图象开口向下,对称轴为直线x=75,所以当x=75时,Smax=625,
即该公司可获得的最大利润为625元,
此时相应的销售单价为75元/件,销售量为25件.
探究点三
[例3] 现计划建造一个室内面积为1 500 m2的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留1.5 m宽的通道,两养殖池之间保留2 m宽的通道.设温室的一边长度为x m,如图所示.
(1)将两个养殖池的总面积y表示为x的函数,并写出定义域;
[例3] 现计划建造一个室内面积为1 500 m2的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留1.5 m宽的通道,两养殖池之间保留2 m宽的通道.设温室的一边长度为x m,如图所示.
(2)当温室的边长x取何值时,总面积y最大 最大值是多少
方法总结
针对训练3:某建筑公司打算在一处工地上修建一座简易储物间.该储物间室内地面呈矩形形状,面积为50 m2,并且一面紧靠工地现有围墙,另三面用高度一定的矩形彩钢板围成,顶部用防雨布遮盖,其平面图如图所示.已知该型号彩钢板价格为100元/米,整理地面及防雨布总费用为500元,不受地形限制,不考虑彩钢板的厚度,记与墙面平行的彩钢板的长度为x m.
(1)用x表示修建储物间的总造价f(x)(单位:元);
针对训练3:某建筑公司打算在一处工地上修建一座简易储物间.该储物间室内地面呈矩形形状,面积为50 m2,并且一面紧靠工地现有围墙,另三面用高度一定的矩形彩钢板围成,顶部用防雨布遮盖,其平面图如图所示.已知该型号彩钢板价格为100元/米,整理地面及防雨布总费用为500元,不受地形限制,不考虑彩钢板的厚度,记与墙面平行的彩钢板的长度为x m.
(2)如何设计该储物间,可使总造价最低 最低总造价为多少元
分段函数模型
探究点四
(1)试写出该超市这种商品的日销售额y与时间t(0(2)求该超市这种商品的日销售额y的最大值与最小值.
解:(2)由(1)知①当0函数图象开口向下,对称轴为直线t=5,该函数在(0,5]上单调递增,在(5,10]上单调递减,
所以ymax=1 225(当t=5时取得),ymin=1 200(当t=10时取得);
②当10由①②知ymax=1 225(当t=5时取得),ymin=600(当t=20时取得).
所以该超市这种商品日销售额的最大值为1 225元,最小值为600元.
方法总结
应用分段函数时的三个注意点
(1)分段函数的“段”一定要分得合理,不重不漏.
(2)分段函数的定义域为对应每一段自变量取值范围的并集.
(3)分段函数的值域求法为逐段求函数值的范围,最后取并集.
(1)写出总成本函数p(x)和利润函数f(x)的解析式;
(2)要使工厂有盈利,生产的产品数量x应控制在什么范围
(3)当生产的产品数量x为何值时,利润最大 最大利润为多少万元
当堂检测
B
1.某公司市场营销人员的个人月收入y(单位:元)与其每月的销售量x(单位:万件)成一次函数关系,其图象如图所示,由图中给出的信息可知,营销人员没有月销售量时的月收入是( )
A.310元 B.300元
C.290元 D.280元
解析:由题意可知,月收入y是月销售量x的一次函数,设y=ax+b(a≠0),将(1,800),(2,1 300)代入得a=500,b=300.故y=500x+300,当x=0时,y=300.故选B.
D
2.一条长为80 cm的铁丝截成两段,分别弯成两个正方形,要使两个正方形的面积和最小,两段铁丝的长度分别是( )
A.10 cm,70 cm B.20 cm,60 cm
C.30 cm,50 cm D.40 cm,40 cm
解析:设其中一个正方形的边长为x cm,则另一个正方形的边长为(20-x)cm.
两个正方形的面积和为S=x2+(20-x)2=2x2-40x+400=2(x-10)2+200,
所以x=10 cm时,两个正方形的面积和最小为200 cm2,此时20-x=10 cm,所以两段铁丝的长度分别是40 cm,40 cm.故选D.
解析:y=x(1+2%)(1-2%),
即y=0.999 6x,x>0.
3.一种商品的售价上涨2%后,又下降了2%,则商品的最终售价y与原来的售价x之间的关系为 .
答案:y=0.999 6x(x>0)
答案:200 10 000元
备用例题
某家庭(父亲、母亲和孩子们)去某地旅游,甲旅行社说:“如果父亲买一张全票,其余人可享受半票优惠.”乙旅行社说:“家庭旅行为集体票,按原价的三分之二优惠.”这两家旅行社的原价是一样的,根据该家庭中孩子数的不同,分别建立表达式,计算两家旅行社的收费,并讨论哪家旅行社更优惠.
3.4 函数的应用(一)
学习目标
1.理解函数是描述客观世界中变量关系和规律的重要数学语言和工具.
2.在实际情境中,会选择合适的函数模型刻画现实问题的变化规律,培养数学建模、数据分析和数学运算素养.
知识梳理·自主探究
师生互动·合作探究
知识梳理·自主探究
知识探究
1.一次函数模型
形如y=kx+b(k≠0)的函数模型是一次函数模型,一次函数的图象为直线,应用一次函数的性质,可以求参数值及函数解析式等.
2.二次函数模型
(1)形如y=ax2+bx+c(a≠0)的函数模型是二次函数模型.
(2)二次函数模型是生活中最常见的一种数学模型,依据实际问题建立二次函数的解析式后,利用配方法求最值简单易懂,有时可以依据二次函数的单调性求最值,从而解决最大、最小等问题.
3.分段函数模型
(1)分段函数模型
分段函数是指函数解析式由几段组成的函数,根据自变量取值范围的不同,由题设确定出不同的函数关系式.
(2)分段函数模型的应用
①分段函数模型应用的关键是确定分段的各边界点.即明确自变量的取值区间,对每一区间进行分类讨论,从而写出函数解析式,需注意分段函数的最值,是各区间上解析式取得的最大值或最小值.
②要注意结合实际问题的实际意义,有时还可结合图象去求解.
师生互动·合作探究
探究点一
一次函数模型
[例1] 甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾,
“龙虾节”期间,甲、乙两家商店都让利酬宾,付款金额y甲,y乙(单位:元)与原价x(单位:元)之间的函数关系如图所示.
(1)写出y甲,y乙关于x的函数关系式;
[例1] 甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾,
“龙虾节”期间,甲、乙两家商店都让利酬宾,付款金额y甲,y乙(单位:元)与原价x(单位:元)之间的函数关系如图所示.
(2)“龙虾节”期间,如何选择甲、乙两家商店购买小龙虾更省钱
解:(2)当0
方法总结
建立一次函数模型,常设为y=kx+b(k≠0),然后用待定系数法求出k,b的值,再根据单调性求最值或利用方程、不等式思想解题.
针对训练1:某长途汽车客运公司规定旅客可随身携带一定质量的行李.若超过规定的质量,则需购买行李票,行李费用y(单位:元)是行李质量x(单位:kg)的一次函数,其图象如图所示.
(1)根据图象数据,求y与x之间的函数关系式;
针对训练1:某长途汽车客运公司规定旅客可随身携带一定质量的行李.若超过规定的质量,则需购买行李票,行李费用y(单位:元)是行李质量x(单位:kg)的一次函数,其图象如图所示.
(2)问旅客最多可免费携带行李的质量是多少
解:(2)根据题意,当y=0时,0≤x≤30.
所以旅客最多可免费携带行李的质量为30 kg.
探究点二
二次函数模型
[例2] 某农家旅游公司有客房160间,每间房单价为200元时,每天都客满.已知每间房单价每提高20元,则客房出租数就会减少10间,若不考虑其他因素,旅游公司把每间房单价提到多少时,每天客房的租金总收入最高
解:设每间房单价提高x个20元时,每天客房的租金总收入为y元.
此时每间房单价为(200+20x)元,而客房出租数将减少10x间,即为(160-10x)间,因此
y=(200+20x)(160-10x)=200(10+x)(16-x)
=200(-x2+6x+160)=200[-(x-3)2+169]=-200(x-3)2+33 800.
从而可知,当x=3时,y的最大值为33 800.
因此每间房单价提到200+20×3=260元时,每天客房的租金总收入最高.
方法总结
(1)二次函数与二次方程之间有密切的关系,解题时要注意题目中的约束
条件.
(2)求解二次函数问题应注意二次函数图象的对称性与单调性.
(3)解决实际生活中用料最省、利润最大等问题时,一般建立二次函数模型,还需掌握一些常见的关系式,如利润=(商品销售单价-商品成本单价)×销售量等.
针对训练2:某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(单位:件)与销售单价x(单位:元/件)的关系可近似看作一次函数y=kx+b(如图所示).
(1)根据图象,求一次函数y=kx+b的解析式;
针对训练2:某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(单位:件)与销售单价x(单位:元/件)的关系可近似看作一次函数y=kx+b(如图所示).
(2)设公司获得的利润为S(单位:元)(利润=销售总价-成本总价,销售总价=销售单价×销售量,成本总价=成本单价×销售量).
①试用销售单价x表示利润S;
解:(2)①由(1)知,S=xy-50y=(-x+100)(x-50)
=-x2+150x-5 000(50≤x≤80).
针对训练2:某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(单位:件)与销售单价x(单位:元/件)的关系可近似看作一次函数y=kx+b(如图所示).
(2)设公司获得的利润为S(单位:元)(利润=销售总价-成本总价,销售总价=销售单价×销售量,成本总价=成本单价×销售量).
②当销售单价定为多少时,该公司可获得最大利润 最大利润是多少 此时的销售量是多少
解:②由①可知,S=-(x-75)2+625(50≤x≤80),
其图象开口向下,对称轴为直线x=75,所以当x=75时,Smax=625,
即该公司可获得的最大利润为625元,
此时相应的销售单价为75元/件,销售量为25件.
探究点三
[例3] 现计划建造一个室内面积为1 500 m2的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留1.5 m宽的通道,两养殖池之间保留2 m宽的通道.设温室的一边长度为x m,如图所示.
(1)将两个养殖池的总面积y表示为x的函数,并写出定义域;
[例3] 现计划建造一个室内面积为1 500 m2的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留1.5 m宽的通道,两养殖池之间保留2 m宽的通道.设温室的一边长度为x m,如图所示.
(2)当温室的边长x取何值时,总面积y最大 最大值是多少
方法总结
针对训练3:某建筑公司打算在一处工地上修建一座简易储物间.该储物间室内地面呈矩形形状,面积为50 m2,并且一面紧靠工地现有围墙,另三面用高度一定的矩形彩钢板围成,顶部用防雨布遮盖,其平面图如图所示.已知该型号彩钢板价格为100元/米,整理地面及防雨布总费用为500元,不受地形限制,不考虑彩钢板的厚度,记与墙面平行的彩钢板的长度为x m.
(1)用x表示修建储物间的总造价f(x)(单位:元);
针对训练3:某建筑公司打算在一处工地上修建一座简易储物间.该储物间室内地面呈矩形形状,面积为50 m2,并且一面紧靠工地现有围墙,另三面用高度一定的矩形彩钢板围成,顶部用防雨布遮盖,其平面图如图所示.已知该型号彩钢板价格为100元/米,整理地面及防雨布总费用为500元,不受地形限制,不考虑彩钢板的厚度,记与墙面平行的彩钢板的长度为x m.
(2)如何设计该储物间,可使总造价最低 最低总造价为多少元
分段函数模型
探究点四
(1)试写出该超市这种商品的日销售额y与时间t(0
解:(2)由(1)知①当0
所以ymax=1 225(当t=5时取得),ymin=1 200(当t=10时取得);
②当10
所以该超市这种商品日销售额的最大值为1 225元,最小值为600元.
方法总结
应用分段函数时的三个注意点
(1)分段函数的“段”一定要分得合理,不重不漏.
(2)分段函数的定义域为对应每一段自变量取值范围的并集.
(3)分段函数的值域求法为逐段求函数值的范围,最后取并集.
(1)写出总成本函数p(x)和利润函数f(x)的解析式;
(2)要使工厂有盈利,生产的产品数量x应控制在什么范围
(3)当生产的产品数量x为何值时,利润最大 最大利润为多少万元
当堂检测
B
1.某公司市场营销人员的个人月收入y(单位:元)与其每月的销售量x(单位:万件)成一次函数关系,其图象如图所示,由图中给出的信息可知,营销人员没有月销售量时的月收入是( )
A.310元 B.300元
C.290元 D.280元
解析:由题意可知,月收入y是月销售量x的一次函数,设y=ax+b(a≠0),将(1,800),(2,1 300)代入得a=500,b=300.故y=500x+300,当x=0时,y=300.故选B.
D
2.一条长为80 cm的铁丝截成两段,分别弯成两个正方形,要使两个正方形的面积和最小,两段铁丝的长度分别是( )
A.10 cm,70 cm B.20 cm,60 cm
C.30 cm,50 cm D.40 cm,40 cm
解析:设其中一个正方形的边长为x cm,则另一个正方形的边长为(20-x)cm.
两个正方形的面积和为S=x2+(20-x)2=2x2-40x+400=2(x-10)2+200,
所以x=10 cm时,两个正方形的面积和最小为200 cm2,此时20-x=10 cm,所以两段铁丝的长度分别是40 cm,40 cm.故选D.
解析:y=x(1+2%)(1-2%),
即y=0.999 6x,x>0.
3.一种商品的售价上涨2%后,又下降了2%,则商品的最终售价y与原来的售价x之间的关系为 .
答案:y=0.999 6x(x>0)
答案:200 10 000元
备用例题
某家庭(父亲、母亲和孩子们)去某地旅游,甲旅行社说:“如果父亲买一张全票,其余人可享受半票优惠.”乙旅行社说:“家庭旅行为集体票,按原价的三分之二优惠.”这两家旅行社的原价是一样的,根据该家庭中孩子数的不同,分别建立表达式,计算两家旅行社的收费,并讨论哪家旅行社更优惠.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
