等腰三角形复习2[上学期]
图片预览





文档简介
课件25张PPT。等腰三角形复习 等腰三角形的性质与判定
1.性质 性质定理:等腰三角形的两个底角相等。 定理:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
2.判定
定义:有两边相等的三角形是等腰三角形。
判定定理:有两个角相等的三角形是等腰三角形。
推论1 三个角都相等的三角形是等边三角形。
推论2 有一个角等于60°的等腰三角形是等边三角形。
推论3 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半等腰三角形性质与判定的应用 (1)计算角的度数 利用等腰三角形的性质,结合三角形内角和定理及推论计算角的度数,是等腰三角形性质的重要应用。 ①已知角的度数,求其它角的度数 ②已知条件中有较多的等腰三角形(此时往往设法用未知数表示图中的角,从中得到含这些未知数的方程或方程组) (2)证明线段或角相等 以等腰三角形为条件时的常用辅助线:
如图:若AB=AC
①作AD⊥BC于D,必有结论:∠1=∠2,BD=DC
②若BD=DC,连结AD,必有结论:∠1=∠2,AD⊥BC
③作AD平分∠BAC必有结论:AD⊥BC,BD=DC
作辅助线时,一定要作满足其中一个性质的辅助线,然后证出其它两个性质,不能这样作:作AD⊥BC,使∠1=∠2. 2. 若等腰三角形的一个内角是45°,则它的顶角为90°( ) 1.若等腰三角形两条边的长分别是5和8,则它的周长为 .21或18总结:在解等腰三角形的题目时,经常会运用
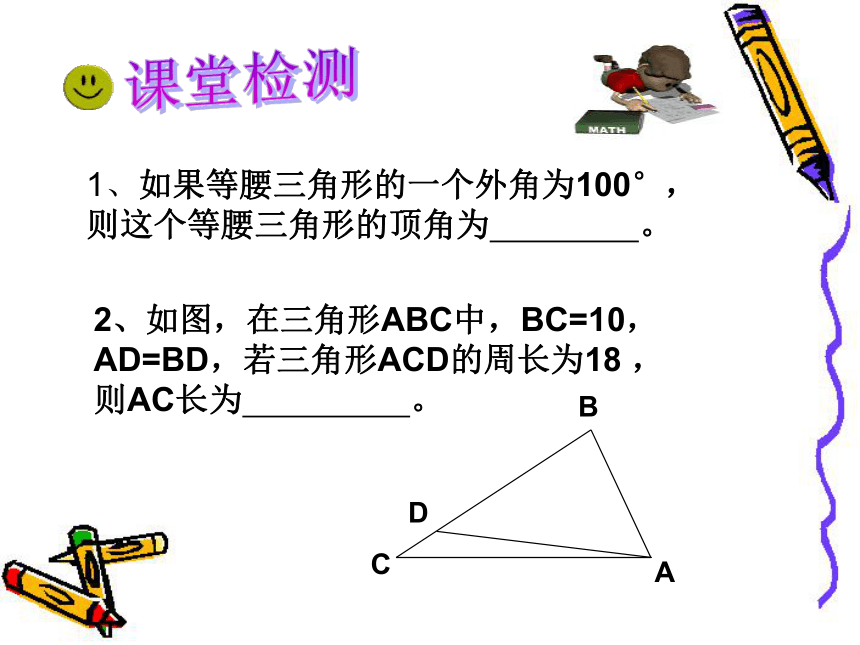
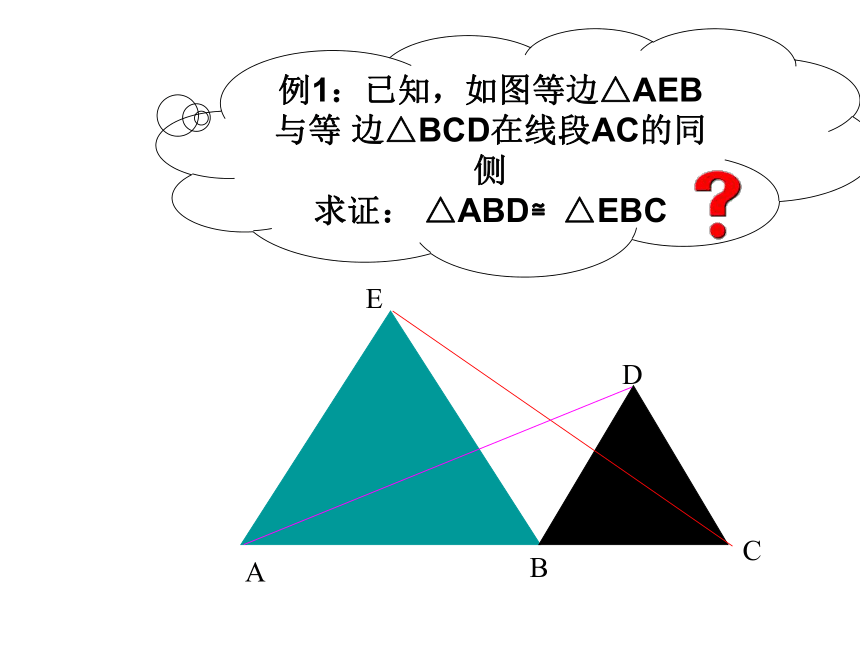
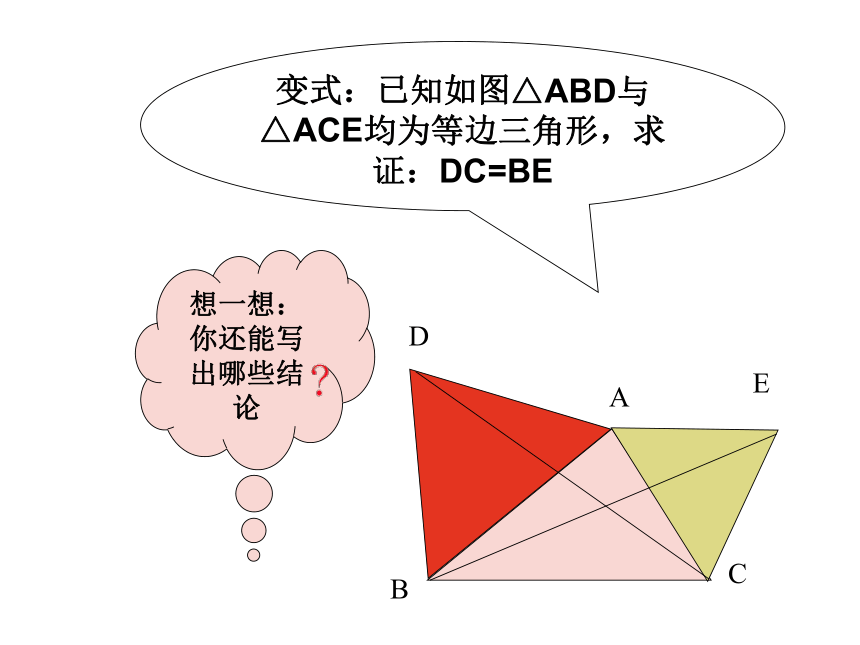
分类思想讨论,以防止掉入数学“陷阱”!1、如果等腰三角形的一个外角为100°, 则这个等腰三角形的顶角为 。2、如图,在三角形ABC中,BC=10,AD=BD,若三角形ACD的周长为18 , 则AC长为 。课堂检测ABCED例1:已知,如图等边△AEB与等 边△BCD在线段AC的同侧 求证: △ABD≌△EBCA B C DE变式:已知如图△ABD与△ACE均为等边三角形,求证:DC=BE想一想:
你还能写出哪些结论
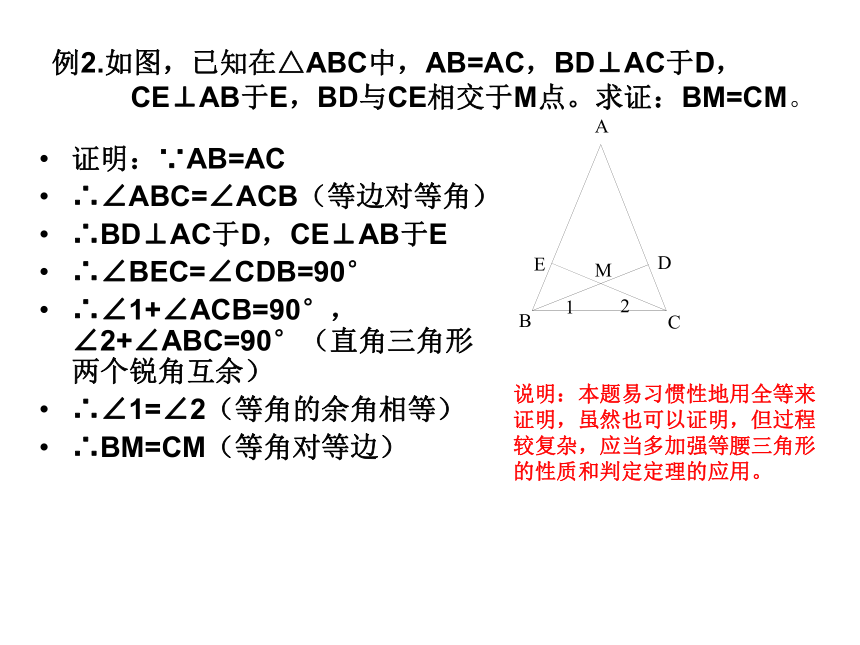
例2.如图,已知在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD与CE相交于M点。求证:BM=CM。证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∴BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠CDB=90°
∴∠1+∠ACB=90°,∠2+∠ABC=90°(直角三角形两个锐角互余)
∴∠1=∠2(等角的余角相等)
∴BM=CM(等角对等边)说明:本题易习惯性地用全等来证明,虽然也可以证明,但过程较复杂,应当多加强等腰三角形的性质和判定定理的应用。例3 已知:如图,∠A=90°,∠B=15°,BD=DC. 求证:AC= BD.证明:
∵BD=DC,∠B=15°
∴∠DCB=∠B=15°(等角对等边)
∴∠ADC=∠B+∠DCB=30°
(三角形的外角等于和它不相邻的两个内角的和)
∵∠A=90°
∴AC= DC
∴AC= BD例4.如图,已知△ABC中,AB=AC,BD=BC,AD=DE=EB. 求∠A的度数.分析:本题有较多的等腰三角形的条件,最好用列方程组的方法来求解,应当在图形上标出各未知数,可使解题过程清晰明了。解:设∠A=x ,∠EBD=y,∠C=z
∵AB=AC
∴∠ABC=∠C=z
∵BD=BC
∴∠C=∠BDC=z
∵BE=DE
∴∠EBD=∠EDB=90°
∵AD=DE
∴∠A=∠AED=x
又∵∠BDC=∠A+∠ABD,∠AED=∠EBD+∠EDB (三角形的外角等于和它不相邻的两个内角的和)
∠A+∠ABC+∠ACB=180°(三角形内角和为180°)
∴解得x=45°
即:∠A=45°例5.已知:如图,∠C=90°,BC=AC,D、E分别在BC和AC上,且BD=CE,M是AB的中点. 求证:△MDE是等腰三角形.分析:要证△MDE是等腰三角形,只需证MD=ME。连结CM,可利用△BMD≌△CME得到结果。证明:连结CM
∵∠C=90°,BC=AC
∴∠A=∠B=45°
∵M是AB的中点
∴CM平分∠BCA(等腰三角形顶角的平分线和底边上的中线重合)
∴∠MCE=∠MCB=∠BCA=45°
∴∠B=∠MCE=∠MCB
∴CM=MB(等角对等边)
在△BDE和△CEM中
∴△BDM≌△CEM(SAS)
∴MD=ME
∴△MDE是等腰三角形例6.如图,在等边△ABC中,AF=BD=CE, 求证:△DEF也是等边三角形.证明:∵△ABC是等边三角形
∴AC=BC,∠A=∠C
∵CE=BD
∴BC-BD=AC-CE
∴CD=AE
在△AEF和△CDE中
∴△AEF≌△CDE(SAS)
∴EF=DE
同理可证EF=DF
∴EF=DE=DF
∴△DEF是等边三角形说明:证明等边三角形有三种思路:
①证明三边相等 ②证明三角相等 ③证明三角形是有一个角为60°的等腰三角形。
具体问题中可利用不同的方式进行求解。例7 如图2-8-1,中,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G 求证:DG=EG思路 因为△GDB和△GEC不全等,所以考虑在△GDB内作出一个与△GEC全等的三角形。 证明:过D作DH∥AE,交BC于H
∴
∵AB=AC ∴
∴
∴DB=DH
又∵DB=CE
∴DH=CE
又∵
∴
∴DG=EG.说明 本题易明显得出DG和EG所在的△DBG和△ECG不全等,故要构造三角形的全等,本题的另一种证法是过E作EF∥BD,交BC的延长线于F,证明△DBG≌△EFG,同学们不妨试一试。例8 如图2-8-6,在△ABC中,AB=AC=CB,AE=CD,AD、BE相交于P,BQ⊥AD于Q. 求证:BP=2PQ思路 在Rt△BPQ中,本题的结论等价于证明∠PBQ=30° 证明 ∵AB=CA,∠BAE=∠ACD=60°,AE=CD,
∴△BAE≌△ACD
∴∠ABE=∠CAD
∴∠BPQ=∠ABE+∠BAP
=∠CAD+∠BAP=60°
又∵BQ⊥AD
∴∠PBQ=30°
∴BP=2PQ说明 本题把证明线段之间的关系转化为证明角的度数,这种转换问题的方法值得同学们细心体会。1.等腰三角形顶角为36°,底角为_________。
2.等腰三角形顶角和一个底角之和为100°,则顶角度数为_____________。
3.等腰三角形两个角之比为4:1,则顶角为__________,底角为___________。
4.等腰三角形两边长为4、6,这个三角形周长为_____________。
5.已知△ABC中AB=AC,AB垂直平分线交AC于E,交AB于D,连结BE,若∠A=50°,∠EBC=__________。
6.△ABC中,AB=AC,AD⊥BC于D,若△ABC的周长为50,△ABD的周长为40,则AD=____________。
7.若等腰三角形顶角为n度,则腰上的高与底边的夹角为_____________。练习8.已知两边及其一边上的高,求作三角形。
9.如图,在△ABC中,AB=AC,点D、E分别在AC、AB上,且BC=BD=DE=EA,求∠A的度数。 在等腰直角三角形中,折出∠CAB的平分线AE,交BC边于点E. C点在AB边上的落点为D,连结DE.
2. 若CE=1,则DE=_____.
3. 你还能找出哪些相等的线段吗? 4. 若AB=6,则△DEB的周长等于多少?
1. DE⊥AB吗?
11DB=______.即:CE=DE=DBAD=AC=BCCABO 等腰直角三角形ABC两底角的平分线AO与BO交于点O, 过O点作底边AB的平行线交AC于点F,交BC于点E. 则:
3. 若AC=10,则△CEF的周长为多少?2. AF、FE、EB三条线段的长度有何关系?1. 图中有几个等腰三角形?
AF+ EB=FE相等角之间的转化相等线段之间的转化如图(二)当AC=12,BC=8.求△CFE的周长?
解:因为OA平分∠CAB.
所以∠FAO=∠OAB.
又因为EF∥AB.
所以∠FOA=∠OAB.
所以∠FAO=∠FOA
即:AF=OF 所以AC=AF+FC=OF+FC.
同理可得:BC=BE+EC=OE+EC.
所以△CFE的周长: =OF+FC+OE+EC
=AC+BC=12+8=20 如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?OD150°⌒CaEFH 请把这个等腰三角形纸片折成两个等腰三角形!36°⌒
ABC请把这个三角形纸片折成两个等腰三角形! 在下图三角形的边上找出一点,使得该点与
三角形的其中两顶点构成等腰三角形!BAC50°110°20°1、对∠A进行讨论2、对∠B进行讨论3、对∠C进行讨论(分类讨论)
1.性质 性质定理:等腰三角形的两个底角相等。 定理:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
2.判定
定义:有两边相等的三角形是等腰三角形。
判定定理:有两个角相等的三角形是等腰三角形。
推论1 三个角都相等的三角形是等边三角形。
推论2 有一个角等于60°的等腰三角形是等边三角形。
推论3 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半等腰三角形性质与判定的应用 (1)计算角的度数 利用等腰三角形的性质,结合三角形内角和定理及推论计算角的度数,是等腰三角形性质的重要应用。 ①已知角的度数,求其它角的度数 ②已知条件中有较多的等腰三角形(此时往往设法用未知数表示图中的角,从中得到含这些未知数的方程或方程组) (2)证明线段或角相等 以等腰三角形为条件时的常用辅助线:
如图:若AB=AC
①作AD⊥BC于D,必有结论:∠1=∠2,BD=DC
②若BD=DC,连结AD,必有结论:∠1=∠2,AD⊥BC
③作AD平分∠BAC必有结论:AD⊥BC,BD=DC
作辅助线时,一定要作满足其中一个性质的辅助线,然后证出其它两个性质,不能这样作:作AD⊥BC,使∠1=∠2. 2. 若等腰三角形的一个内角是45°,则它的顶角为90°( ) 1.若等腰三角形两条边的长分别是5和8,则它的周长为 .21或18总结:在解等腰三角形的题目时,经常会运用
分类思想讨论,以防止掉入数学“陷阱”!1、如果等腰三角形的一个外角为100°, 则这个等腰三角形的顶角为 。2、如图,在三角形ABC中,BC=10,AD=BD,若三角形ACD的周长为18 , 则AC长为 。课堂检测ABCED例1:已知,如图等边△AEB与等 边△BCD在线段AC的同侧 求证: △ABD≌△EBCA B C DE变式:已知如图△ABD与△ACE均为等边三角形,求证:DC=BE想一想:
你还能写出哪些结论
例2.如图,已知在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD与CE相交于M点。求证:BM=CM。证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∴BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠CDB=90°
∴∠1+∠ACB=90°,∠2+∠ABC=90°(直角三角形两个锐角互余)
∴∠1=∠2(等角的余角相等)
∴BM=CM(等角对等边)说明:本题易习惯性地用全等来证明,虽然也可以证明,但过程较复杂,应当多加强等腰三角形的性质和判定定理的应用。例3 已知:如图,∠A=90°,∠B=15°,BD=DC. 求证:AC= BD.证明:
∵BD=DC,∠B=15°
∴∠DCB=∠B=15°(等角对等边)
∴∠ADC=∠B+∠DCB=30°
(三角形的外角等于和它不相邻的两个内角的和)
∵∠A=90°
∴AC= DC
∴AC= BD例4.如图,已知△ABC中,AB=AC,BD=BC,AD=DE=EB. 求∠A的度数.分析:本题有较多的等腰三角形的条件,最好用列方程组的方法来求解,应当在图形上标出各未知数,可使解题过程清晰明了。解:设∠A=x ,∠EBD=y,∠C=z
∵AB=AC
∴∠ABC=∠C=z
∵BD=BC
∴∠C=∠BDC=z
∵BE=DE
∴∠EBD=∠EDB=90°
∵AD=DE
∴∠A=∠AED=x
又∵∠BDC=∠A+∠ABD,∠AED=∠EBD+∠EDB (三角形的外角等于和它不相邻的两个内角的和)
∠A+∠ABC+∠ACB=180°(三角形内角和为180°)
∴解得x=45°
即:∠A=45°例5.已知:如图,∠C=90°,BC=AC,D、E分别在BC和AC上,且BD=CE,M是AB的中点. 求证:△MDE是等腰三角形.分析:要证△MDE是等腰三角形,只需证MD=ME。连结CM,可利用△BMD≌△CME得到结果。证明:连结CM
∵∠C=90°,BC=AC
∴∠A=∠B=45°
∵M是AB的中点
∴CM平分∠BCA(等腰三角形顶角的平分线和底边上的中线重合)
∴∠MCE=∠MCB=∠BCA=45°
∴∠B=∠MCE=∠MCB
∴CM=MB(等角对等边)
在△BDE和△CEM中
∴△BDM≌△CEM(SAS)
∴MD=ME
∴△MDE是等腰三角形例6.如图,在等边△ABC中,AF=BD=CE, 求证:△DEF也是等边三角形.证明:∵△ABC是等边三角形
∴AC=BC,∠A=∠C
∵CE=BD
∴BC-BD=AC-CE
∴CD=AE
在△AEF和△CDE中
∴△AEF≌△CDE(SAS)
∴EF=DE
同理可证EF=DF
∴EF=DE=DF
∴△DEF是等边三角形说明:证明等边三角形有三种思路:
①证明三边相等 ②证明三角相等 ③证明三角形是有一个角为60°的等腰三角形。
具体问题中可利用不同的方式进行求解。例7 如图2-8-1,中,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G 求证:DG=EG思路 因为△GDB和△GEC不全等,所以考虑在△GDB内作出一个与△GEC全等的三角形。 证明:过D作DH∥AE,交BC于H
∴
∵AB=AC ∴
∴
∴DB=DH
又∵DB=CE
∴DH=CE
又∵
∴
∴DG=EG.说明 本题易明显得出DG和EG所在的△DBG和△ECG不全等,故要构造三角形的全等,本题的另一种证法是过E作EF∥BD,交BC的延长线于F,证明△DBG≌△EFG,同学们不妨试一试。例8 如图2-8-6,在△ABC中,AB=AC=CB,AE=CD,AD、BE相交于P,BQ⊥AD于Q. 求证:BP=2PQ思路 在Rt△BPQ中,本题的结论等价于证明∠PBQ=30° 证明 ∵AB=CA,∠BAE=∠ACD=60°,AE=CD,
∴△BAE≌△ACD
∴∠ABE=∠CAD
∴∠BPQ=∠ABE+∠BAP
=∠CAD+∠BAP=60°
又∵BQ⊥AD
∴∠PBQ=30°
∴BP=2PQ说明 本题把证明线段之间的关系转化为证明角的度数,这种转换问题的方法值得同学们细心体会。1.等腰三角形顶角为36°,底角为_________。
2.等腰三角形顶角和一个底角之和为100°,则顶角度数为_____________。
3.等腰三角形两个角之比为4:1,则顶角为__________,底角为___________。
4.等腰三角形两边长为4、6,这个三角形周长为_____________。
5.已知△ABC中AB=AC,AB垂直平分线交AC于E,交AB于D,连结BE,若∠A=50°,∠EBC=__________。
6.△ABC中,AB=AC,AD⊥BC于D,若△ABC的周长为50,△ABD的周长为40,则AD=____________。
7.若等腰三角形顶角为n度,则腰上的高与底边的夹角为_____________。练习8.已知两边及其一边上的高,求作三角形。
9.如图,在△ABC中,AB=AC,点D、E分别在AC、AB上,且BC=BD=DE=EA,求∠A的度数。 在等腰直角三角形中,折出∠CAB的平分线AE,交BC边于点E. C点在AB边上的落点为D,连结DE.
2. 若CE=1,则DE=_____.
3. 你还能找出哪些相等的线段吗? 4. 若AB=6,则△DEB的周长等于多少?
1. DE⊥AB吗?
11DB=______.即:CE=DE=DBAD=AC=BCCABO 等腰直角三角形ABC两底角的平分线AO与BO交于点O, 过O点作底边AB的平行线交AC于点F,交BC于点E. 则:
3. 若AC=10,则△CEF的周长为多少?2. AF、FE、EB三条线段的长度有何关系?1. 图中有几个等腰三角形?
AF+ EB=FE相等角之间的转化相等线段之间的转化如图(二)当AC=12,BC=8.求△CFE的周长?
解:因为OA平分∠CAB.
所以∠FAO=∠OAB.
又因为EF∥AB.
所以∠FOA=∠OAB.
所以∠FAO=∠FOA
即:AF=OF 所以AC=AF+FC=OF+FC.
同理可得:BC=BE+EC=OE+EC.
所以△CFE的周长: =OF+FC+OE+EC
=AC+BC=12+8=20 如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?OD150°⌒CaEFH 请把这个等腰三角形纸片折成两个等腰三角形!36°⌒
ABC请把这个三角形纸片折成两个等腰三角形! 在下图三角形的边上找出一点,使得该点与
三角形的其中两顶点构成等腰三角形!BAC50°110°20°1、对∠A进行讨论2、对∠B进行讨论3、对∠C进行讨论(分类讨论)
