等腰三角形和直角三角形[上学期]
文档属性
| 名称 | 等腰三角形和直角三角形[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 280.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-16 00:00:00 | ||
图片预览





文档简介
课件28张PPT。等腰三角形与直角三角形(一)数学 初二一、提出问题:
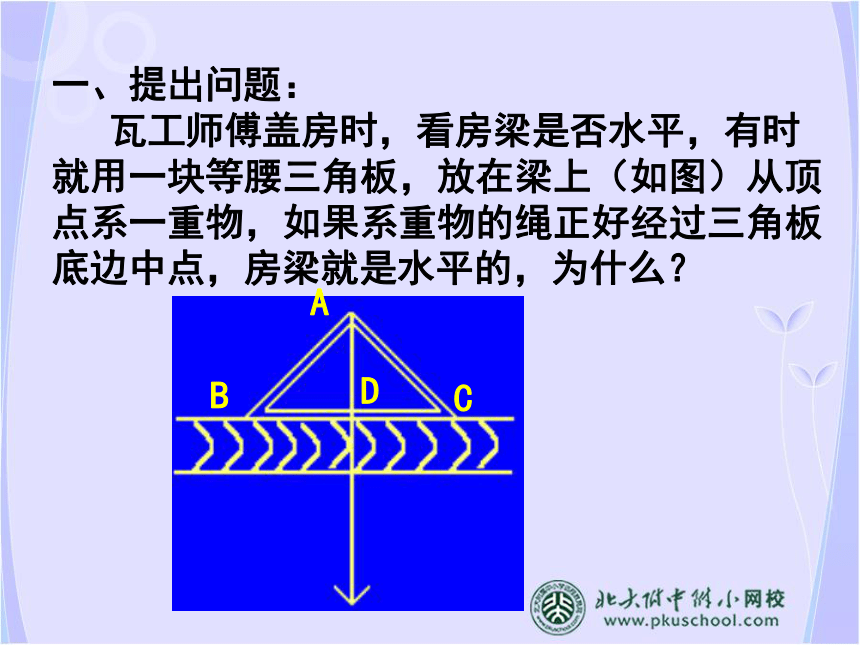
瓦工师傅盖房时,看房梁是否水平,有时
就用一块等腰三角板,放在梁上(如图)从顶点系一重物,如果系重物的绳正好经过三角板底边中点,房梁就是水平的,为什么?二、问题的解决
等腰三角形的性质:
1.等腰三角形的两个底角相等。(简写成“等边对等角)
注意:“等边对等角”是指同一三角形中的边角关系。
2.等腰三角形顶角的平分线平分底边并且垂直于底边。问题解决:若系重物的绳经过BC中点,根据等腰三角形“三线合一”的性质,有AD⊥BC,因为AD是竖直向下,垂直于地面,所以此时房梁是水平的。
等腰三角形的“三线合一”的性质提供了构造直角三角形及证明垂直的方法。三、例题解析
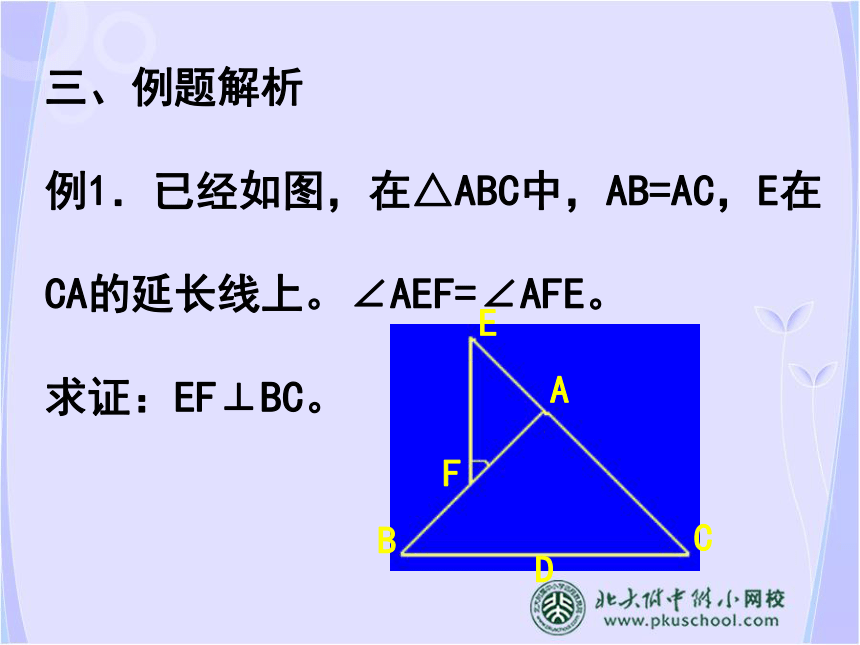
例1.已经如图,在△ABC中,AB=AC,E在
CA的延长线上。∠AEF=∠AFE。
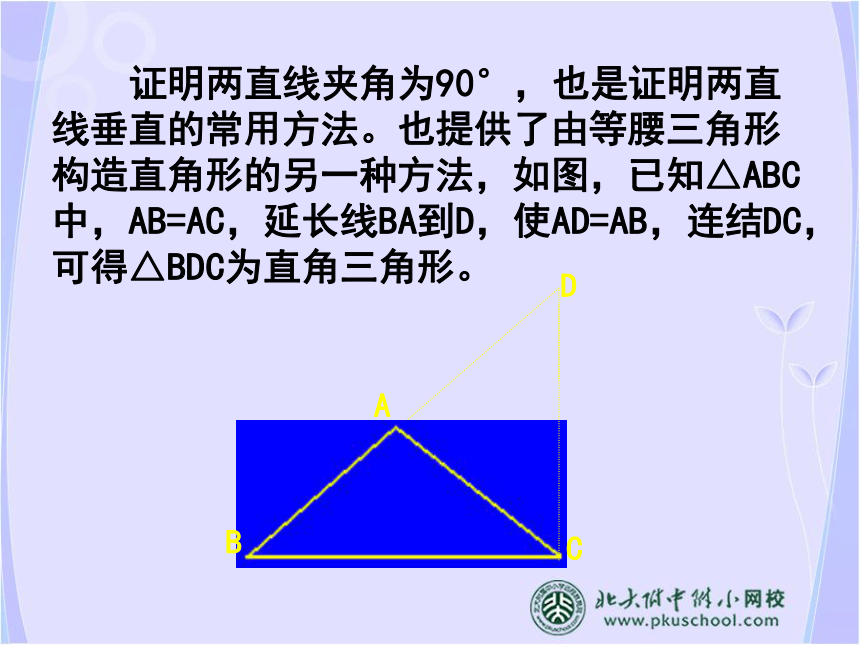
求证:EF⊥BC。∴EF⊥BC。证法一、作BC边上的高AD,D为垂足。∵AB=AC,AD⊥BC∴∠BAC=2∠1又∵∠BAC是△AEF的一个外角,∠E=∠3∴∠BAC=∠E+∠3=2∠3∴2∠1=2∠3∴AD//EF231∴EF⊥BC证法二、过E作EM//BC交BA的延长线于M∵AB=AC∴∠B=∠C∴∠1=∠C,∠B=∠M∴∠1=∠M∵在△EFM中,∠M+∠MEF+∠EFM=180°即∠M+∠1+∠2+∠3=180°∵∠2=∠3∴2(∠1+∠2)=180°即∠1+∠2=90°∴EF⊥EMM123 证明两直线夹角为90°,也是证明两直线垂直的常用方法。也提供了由等腰三角形构造直角形的另一种方法,如图,已知△ABC中,AB=AC,延长线BA到D,使AD=AB,连结DC,可得△BDC为直角三角形。D例题解析
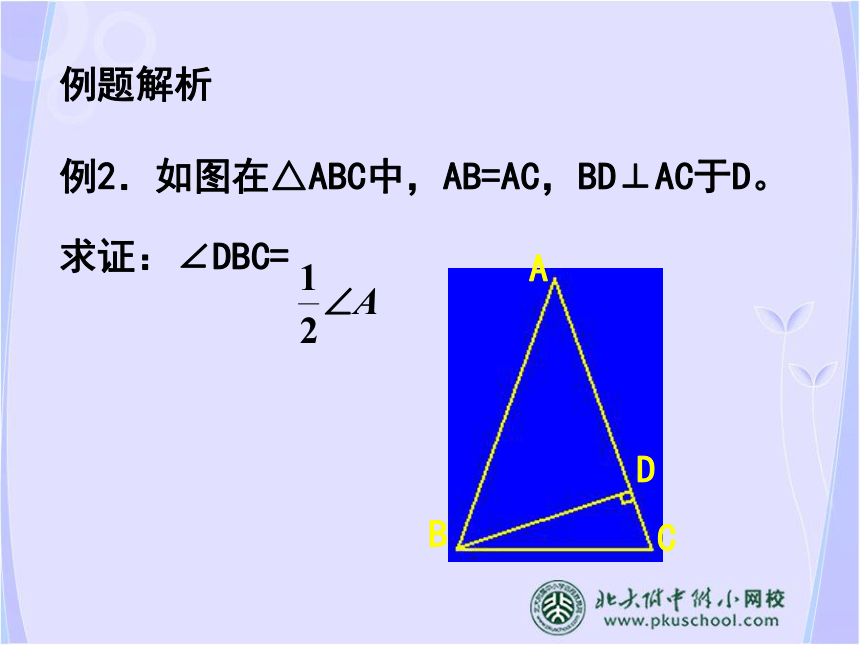
例2.如图在△ABC中,AB=AC,BD⊥AC于D。
求证:∠DBC=证法一:∵在△ABC中,AB=AC,∵BD⊥AC于D证法三:如图,作AE⊥BC于E∵AB=AC∵BD⊥AC于D∴∠DBC+∠C=90°∴∠1=∠DBC(折半法)1证法二:(加倍法) 如图作∠C′BD=∠CBD,交AC于C′∴C′B=CB∵BD⊥AC∴∠C′BC=2∠DBC=180°-2∠C∵AB=AC∴∠ABC=∠C∴∠A=180°-2∠C∴∠C′BC=∠AC′例3.已知,如图△ABC是等边三角形,AE平分∠BAC交BC于E,以BE为边向△ABC的外部作等边△BED。
求证:BD⊥CD
∴BD⊥CD证明:∵△ABC是等边三角形,AE平分∠BAC交BC于E∴BE=EC∵△BED为等边△∴∠1=∠2=60°BE=ED∴DE=EC∴∠3=∠4∵∠2=∠3+∠4∴∠3=30°∴∠BDC=∠1+∠3=60°+30°=90°2341例4.在等腰Rt△ABC中,∠C=90°,D是AB边上任一点。
AE⊥CD于E,CH⊥AB于H,交AE于G
求证:BD=CG∵AE⊥CD于E证明:∵在等腰Rt△ABC中,∠C=90°∴∠CAB=45°∵CH⊥AB于H∴∠1=45°,AH=BH∴∠1=∠CAB∴CH=AH=BH4123∴∠2+∠3=90°∴BD=CG∵∠4+∠3=90°∴∠2=∠4∴在△DHC和△GHA中∴△DHC≌△GHA(ASA)∴DH=GH∴BH-DH=CH―GH例5.如图在△ABC中,∠A=90°,AB=AC,BE平分∠ABC交AC于D,CE⊥BE于E。
求证:CE= 。∴∠3=∠1证明:延长BA、CE交于M点∵BE平分∠ABC∴∠1=∠2∵BE⊥CE∴∠2+∠BCE=90°,∠1+∠M=90°∴∠M=∠BCE∴BC=BM∴CE=∵AB⊥AB∴∠3+∠M=90°1M23等腰直角三角形为我们证明三角形全等提供了条件。在△ACM和△ABD中∴△ACM≌△ABD(ASA)∴BD=CM四、问题探究
现在有一块长方形木板的残留部分,它的两条对边AB、CD整齐且平行,但另两条对边参差不齐,现在没有直角尺,请你在毛边附近画出一条与AB、CD都垂直的边来。由例1中方法二的证明可知FN⊥AB。解:(1)在AB边上靠近A、B的位置分别取点E、F(2)以E、F为圆心,EF长为半径画弧相交于M点(3)以M为圆心,EF长为半径画弧,
交EM的延长线于N(4)连结FN(5)延长FN交CD于KEMNFK五、作业
1.如图,在△ABC中,∠C=∠ABC=2∠A
BD是AC边上的高
求∠DBC的度数
2.如图在△ABC中,已知AB=AC,∠BAC=90°。D是BC上一点,EC⊥BC,EC=BD,DF=FE。
求证:AF⊥DE3.某中学师生在工厂参观中,看到工人师傅在材料的边角处画直角时,用“三弧法”。方法如下(如图)
(1)画线段AB,分别以A、B为圆心,AB长为半径画弧相交于C。
(2)以C为圆心,仍以AB长为半径画弧交AC延长线于D
(3)连结DB
请问∠ABD是△直角吗,为什么?C参考答案
1.18°
2.证明:∵在△ABC中,AB=AC,∠BAC=90°
∴∠B=∠1=45°
∵EC⊥BC
∴∠2=45°
∴∠2=∠B在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴AD=AE
∵DF=FE
∴AF⊥DE
3.参考例1证法二。再见教师:白芳
瓦工师傅盖房时,看房梁是否水平,有时
就用一块等腰三角板,放在梁上(如图)从顶点系一重物,如果系重物的绳正好经过三角板底边中点,房梁就是水平的,为什么?二、问题的解决
等腰三角形的性质:
1.等腰三角形的两个底角相等。(简写成“等边对等角)
注意:“等边对等角”是指同一三角形中的边角关系。
2.等腰三角形顶角的平分线平分底边并且垂直于底边。问题解决:若系重物的绳经过BC中点,根据等腰三角形“三线合一”的性质,有AD⊥BC,因为AD是竖直向下,垂直于地面,所以此时房梁是水平的。
等腰三角形的“三线合一”的性质提供了构造直角三角形及证明垂直的方法。三、例题解析
例1.已经如图,在△ABC中,AB=AC,E在
CA的延长线上。∠AEF=∠AFE。
求证:EF⊥BC。∴EF⊥BC。证法一、作BC边上的高AD,D为垂足。∵AB=AC,AD⊥BC∴∠BAC=2∠1又∵∠BAC是△AEF的一个外角,∠E=∠3∴∠BAC=∠E+∠3=2∠3∴2∠1=2∠3∴AD//EF231∴EF⊥BC证法二、过E作EM//BC交BA的延长线于M∵AB=AC∴∠B=∠C∴∠1=∠C,∠B=∠M∴∠1=∠M∵在△EFM中,∠M+∠MEF+∠EFM=180°即∠M+∠1+∠2+∠3=180°∵∠2=∠3∴2(∠1+∠2)=180°即∠1+∠2=90°∴EF⊥EMM123 证明两直线夹角为90°,也是证明两直线垂直的常用方法。也提供了由等腰三角形构造直角形的另一种方法,如图,已知△ABC中,AB=AC,延长线BA到D,使AD=AB,连结DC,可得△BDC为直角三角形。D例题解析
例2.如图在△ABC中,AB=AC,BD⊥AC于D。
求证:∠DBC=证法一:∵在△ABC中,AB=AC,∵BD⊥AC于D证法三:如图,作AE⊥BC于E∵AB=AC∵BD⊥AC于D∴∠DBC+∠C=90°∴∠1=∠DBC(折半法)1证法二:(加倍法) 如图作∠C′BD=∠CBD,交AC于C′∴C′B=CB∵BD⊥AC∴∠C′BC=2∠DBC=180°-2∠C∵AB=AC∴∠ABC=∠C∴∠A=180°-2∠C∴∠C′BC=∠AC′例3.已知,如图△ABC是等边三角形,AE平分∠BAC交BC于E,以BE为边向△ABC的外部作等边△BED。
求证:BD⊥CD
∴BD⊥CD证明:∵△ABC是等边三角形,AE平分∠BAC交BC于E∴BE=EC∵△BED为等边△∴∠1=∠2=60°BE=ED∴DE=EC∴∠3=∠4∵∠2=∠3+∠4∴∠3=30°∴∠BDC=∠1+∠3=60°+30°=90°2341例4.在等腰Rt△ABC中,∠C=90°,D是AB边上任一点。
AE⊥CD于E,CH⊥AB于H,交AE于G
求证:BD=CG∵AE⊥CD于E证明:∵在等腰Rt△ABC中,∠C=90°∴∠CAB=45°∵CH⊥AB于H∴∠1=45°,AH=BH∴∠1=∠CAB∴CH=AH=BH4123∴∠2+∠3=90°∴BD=CG∵∠4+∠3=90°∴∠2=∠4∴在△DHC和△GHA中∴△DHC≌△GHA(ASA)∴DH=GH∴BH-DH=CH―GH例5.如图在△ABC中,∠A=90°,AB=AC,BE平分∠ABC交AC于D,CE⊥BE于E。
求证:CE= 。∴∠3=∠1证明:延长BA、CE交于M点∵BE平分∠ABC∴∠1=∠2∵BE⊥CE∴∠2+∠BCE=90°,∠1+∠M=90°∴∠M=∠BCE∴BC=BM∴CE=∵AB⊥AB∴∠3+∠M=90°1M23等腰直角三角形为我们证明三角形全等提供了条件。在△ACM和△ABD中∴△ACM≌△ABD(ASA)∴BD=CM四、问题探究
现在有一块长方形木板的残留部分,它的两条对边AB、CD整齐且平行,但另两条对边参差不齐,现在没有直角尺,请你在毛边附近画出一条与AB、CD都垂直的边来。由例1中方法二的证明可知FN⊥AB。解:(1)在AB边上靠近A、B的位置分别取点E、F(2)以E、F为圆心,EF长为半径画弧相交于M点(3)以M为圆心,EF长为半径画弧,
交EM的延长线于N(4)连结FN(5)延长FN交CD于KEMNFK五、作业
1.如图,在△ABC中,∠C=∠ABC=2∠A
BD是AC边上的高
求∠DBC的度数
2.如图在△ABC中,已知AB=AC,∠BAC=90°。D是BC上一点,EC⊥BC,EC=BD,DF=FE。
求证:AF⊥DE3.某中学师生在工厂参观中,看到工人师傅在材料的边角处画直角时,用“三弧法”。方法如下(如图)
(1)画线段AB,分别以A、B为圆心,AB长为半径画弧相交于C。
(2)以C为圆心,仍以AB长为半径画弧交AC延长线于D
(3)连结DB
请问∠ABD是△直角吗,为什么?C参考答案
1.18°
2.证明:∵在△ABC中,AB=AC,∠BAC=90°
∴∠B=∠1=45°
∵EC⊥BC
∴∠2=45°
∴∠2=∠B在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴AD=AE
∵DF=FE
∴AF⊥DE
3.参考例1证法二。再见教师:白芳
