等腰三角形[上学期]
图片预览





文档简介
课件18张PPT。等腰三角形的判定授课老师:杨辉1.什么叫等腰三角形?答:有两边相等的三角形叫做等腰三角形.2.等腰三角形有哪些性质?(1)等腰三角形的两个底角相等。一、概念回顾(2)等腰三角形顶角平分线,底边上中线和高线互相重合。(3)等腰三角形是轴对称图形,对称轴是底边的中垂线。等腰三角形的判定:
?等角对等边;
?有两边相等;
?“三线合一”的逆定理.等边三角形的性质:
?三边相等,三个角都是60o;
?内心和外心重合;
?是轴对称图形,有三条对称轴。等边三角形的判定:
?三条边都相等的三角形;
?三个角都相等的三角形;
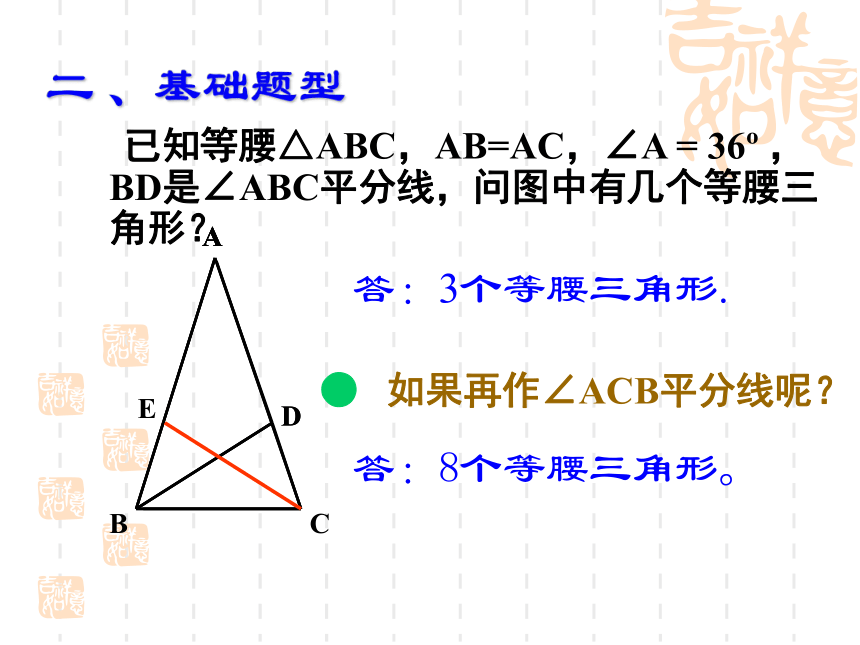
?有一个角是60o的等腰三角形.ACD 已知等腰△ABC,AB=AC,∠A = 36o ,BD是∠ABC平分线,问图中有几个等腰三角形?
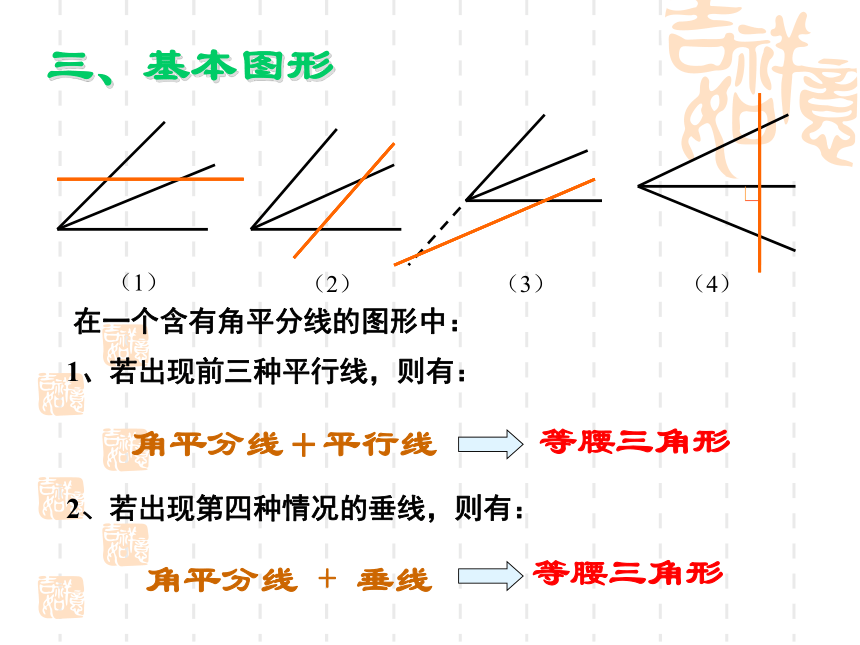
A答:3个等腰三角形.● 如果再作∠ACB平分线呢?答:8个等腰三角形。ADBAE二 、基础题型 在一个含有角平分线的图形中:等腰三角形 角平分线+平行线三、基本图形1、若出现前三种平行线,则有:2、若出现第四种情况的垂线,则有:角平分线 + 垂线等腰三角形(2)(1)(3)(4)例1 已知:ABC,CE、CG分别平分 ACB和 ACD,
EG ∥BD,求 证:EF=GFABCEFG证明:EG ∥BDEF=FC同理:FG=FCEF=FG 41235∠1=∠5∠1=∠2∠2=∠5D分析: 能否直接证明 EF = GF?四、例题例 2、如图,已知:∠1 = ∠2 , AE⊥BE ,
E 是 DC 的中点 ,求证:AB = AD + BC ABD12 EC方法1:截长法)
F在AB上截取AF=AD,连结EF,3456先证 △ADE≌△AFE ∠3=∠4
AF=AD再证 ∠5=∠6后证 △EFB≌△ECBFB=BC∟(注:该题可用多种方法证明)ABCD 12 EF 延长BE交AD的延长线于F,等腰△FAB AB=AF DF=BC△DEF≌△CEB先证 ∠1=∠2
AE⊥BE再证证法 2:补短法∟ 例 2 如图,已知:∠1 = ∠2 , AE⊥BE ,
E 是 DC 的中点 ,求证:AB = AD + BC 得出AF=AD+BC3、如图,已知:A是直线MN上的一点,AD、AC分别是?BAN和?BAM的角平分线,KL∥MN,并分别与AC、AB、AD相交于K、P、L,求证:KP=PL.分析:本题的条件只有两类,角平分线和平行线,因此容易找出它的基本图形是等腰三角形,从而证明,AP=PL,同理可证:AP=KP ∴KP=PL 证明:∵AD是?BAN的平分线 ∴ ?1=?2
又∵ KL∥MN ∴?2=?3
∴?1=?3 ∴AP=PL
同理可证;AP=KP ∴KP=PL基本题扫描例如、如图,点D是△ABC的BC边的中点,M、N分别是边AB和AC上的点,且DM⊥DN. 求证:BM+CN>MN.分析:由点D是BC边的中点,可延长MD至E,使DE=DM,连接NE、CE,易知MN=NE,且△BDM≌△CDE.从而可知BM=EC,
这样BM+CN=EC+CN >NE=MN.E 如图,已知三角形ABC中,AD垂直于∠C 的平分线于D,DE∥BC交AB于E.
求证:EA=EBF分析:等腰三角形具有“顶角平分线垂直平分底边”的性质若“三线合一”,则三角形必为等腰三角形。因此,可延长AD构造出等腰三角形。中考链接 (2004泉州)我们来探究“雪花曲线”的有关问题,图中是边长为1的正三角形,将此正三角形的每条边三等分,以居中的线段为底再作正三角形,然后以其两腰代替底边,得到第二个图形,重复上述的作法得到第三个图形,则得到第五个图形的周长应等于( )析解:从第一个图开始,每进行一次操作,所得
图形的周长是原来的 倍,所以第二个图形的
周长为 ;第三个图形的周长为
第四个图形的周长为 第五个图形的周
长为 因此选B. 这是一道与三角形的周长有关的探索型 问题,我们要发现规律,根据规律解决问题五、课堂练习1.等腰三角形一边长等于4cm,一边长等于9cm,则周长为2. △ABC中, ∠A的外角平分线AE ∥BC,则△ABC是 三角形22cm等腰3.如图,△ABC中,AD平分∠BAC交BC于点D,
DE ∥AC,若DE=5cm,则AE=5cmACEBD5. 如图,AB=AC, ∠A=40°,AB的垂直平
分线MN交AC于点D,则∠DBC=30°4.如图,△ABC中, AB=AC, D在BC上,且
AD=BD,AC=CD,则∠ABC=36°ABDCABCMND谢谢,再见!
?等角对等边;
?有两边相等;
?“三线合一”的逆定理.等边三角形的性质:
?三边相等,三个角都是60o;
?内心和外心重合;
?是轴对称图形,有三条对称轴。等边三角形的判定:
?三条边都相等的三角形;
?三个角都相等的三角形;
?有一个角是60o的等腰三角形.ACD 已知等腰△ABC,AB=AC,∠A = 36o ,BD是∠ABC平分线,问图中有几个等腰三角形?
A答:3个等腰三角形.● 如果再作∠ACB平分线呢?答:8个等腰三角形。ADBAE二 、基础题型 在一个含有角平分线的图形中:等腰三角形 角平分线+平行线三、基本图形1、若出现前三种平行线,则有:2、若出现第四种情况的垂线,则有:角平分线 + 垂线等腰三角形(2)(1)(3)(4)例1 已知:ABC,CE、CG分别平分 ACB和 ACD,
EG ∥BD,求 证:EF=GFABCEFG证明:EG ∥BDEF=FC同理:FG=FCEF=FG 41235∠1=∠5∠1=∠2∠2=∠5D分析: 能否直接证明 EF = GF?四、例题例 2、如图,已知:∠1 = ∠2 , AE⊥BE ,
E 是 DC 的中点 ,求证:AB = AD + BC ABD12 EC方法1:截长法)
F在AB上截取AF=AD,连结EF,3456先证 △ADE≌△AFE ∠3=∠4
AF=AD再证 ∠5=∠6后证 △EFB≌△ECBFB=BC∟(注:该题可用多种方法证明)ABCD 12 EF 延长BE交AD的延长线于F,等腰△FAB AB=AF DF=BC△DEF≌△CEB先证 ∠1=∠2
AE⊥BE再证证法 2:补短法∟ 例 2 如图,已知:∠1 = ∠2 , AE⊥BE ,
E 是 DC 的中点 ,求证:AB = AD + BC 得出AF=AD+BC3、如图,已知:A是直线MN上的一点,AD、AC分别是?BAN和?BAM的角平分线,KL∥MN,并分别与AC、AB、AD相交于K、P、L,求证:KP=PL.分析:本题的条件只有两类,角平分线和平行线,因此容易找出它的基本图形是等腰三角形,从而证明,AP=PL,同理可证:AP=KP ∴KP=PL 证明:∵AD是?BAN的平分线 ∴ ?1=?2
又∵ KL∥MN ∴?2=?3
∴?1=?3 ∴AP=PL
同理可证;AP=KP ∴KP=PL基本题扫描例如、如图,点D是△ABC的BC边的中点,M、N分别是边AB和AC上的点,且DM⊥DN. 求证:BM+CN>MN.分析:由点D是BC边的中点,可延长MD至E,使DE=DM,连接NE、CE,易知MN=NE,且△BDM≌△CDE.从而可知BM=EC,
这样BM+CN=EC+CN >NE=MN.E 如图,已知三角形ABC中,AD垂直于∠C 的平分线于D,DE∥BC交AB于E.
求证:EA=EBF分析:等腰三角形具有“顶角平分线垂直平分底边”的性质若“三线合一”,则三角形必为等腰三角形。因此,可延长AD构造出等腰三角形。中考链接 (2004泉州)我们来探究“雪花曲线”的有关问题,图中是边长为1的正三角形,将此正三角形的每条边三等分,以居中的线段为底再作正三角形,然后以其两腰代替底边,得到第二个图形,重复上述的作法得到第三个图形,则得到第五个图形的周长应等于( )析解:从第一个图开始,每进行一次操作,所得
图形的周长是原来的 倍,所以第二个图形的
周长为 ;第三个图形的周长为
第四个图形的周长为 第五个图形的周
长为 因此选B. 这是一道与三角形的周长有关的探索型 问题,我们要发现规律,根据规律解决问题五、课堂练习1.等腰三角形一边长等于4cm,一边长等于9cm,则周长为2. △ABC中, ∠A的外角平分线AE ∥BC,则△ABC是 三角形22cm等腰3.如图,△ABC中,AD平分∠BAC交BC于点D,
DE ∥AC,若DE=5cm,则AE=5cmACEBD5. 如图,AB=AC, ∠A=40°,AB的垂直平
分线MN交AC于点D,则∠DBC=30°4.如图,△ABC中, AB=AC, D在BC上,且
AD=BD,AC=CD,则∠ABC=36°ABDCABCMND谢谢,再见!
