等腰三角形的性质复习课[上学期]
文档属性
| 名称 | 等腰三角形的性质复习课[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 378.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-16 00:00:00 | ||
图片预览



文档简介
课件15张PPT。14.3.2 等腰三角形(2)
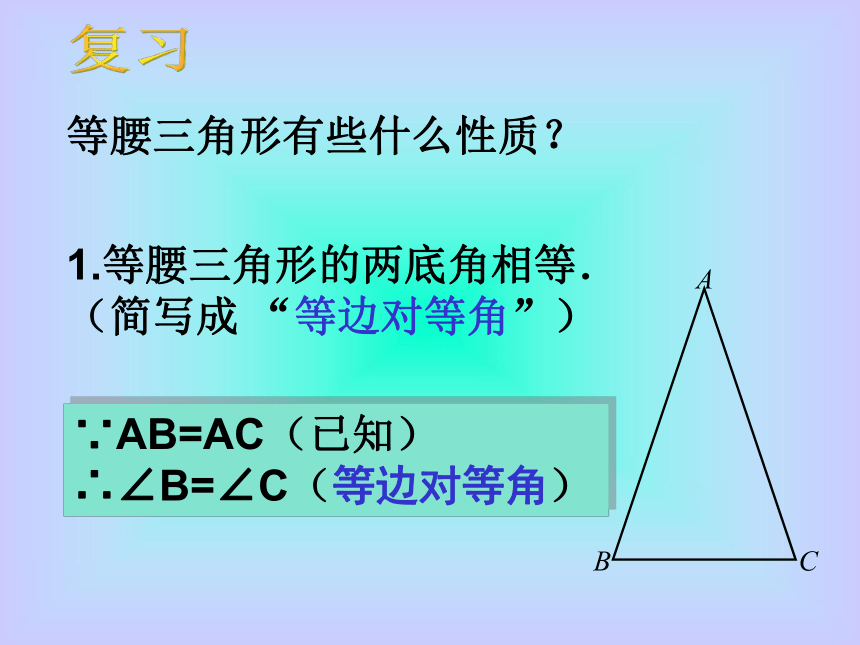
等腰三角形有些什么性质?1.等腰三角形的两底角相等.
(简写成 “等边对等角”) ∵AB=AC(已知)
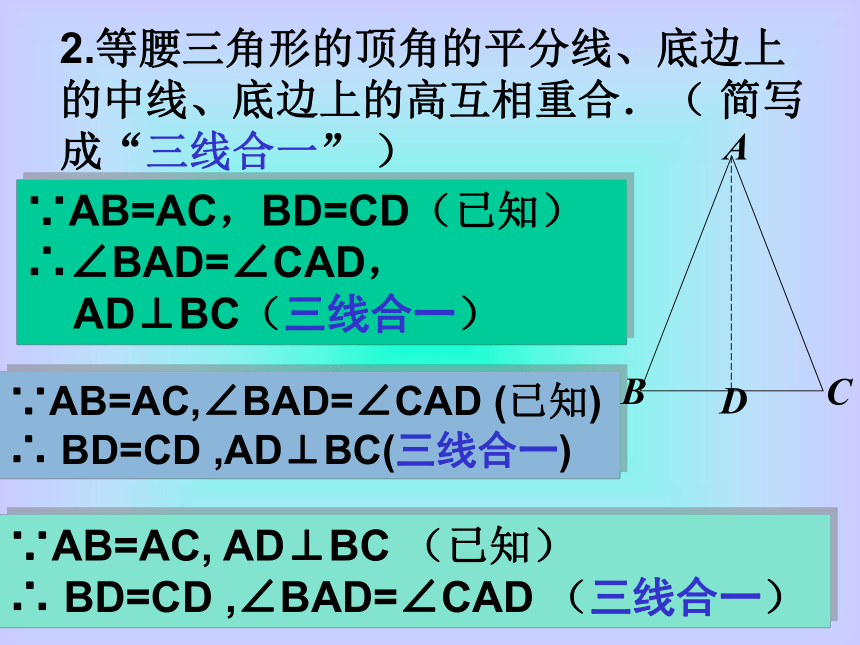
∴∠B=∠C(等边对等角)复习2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.( 简写成“三线合一” )∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(三线合一)∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(三线合一)∵AB=AC, AD⊥BC (已知)
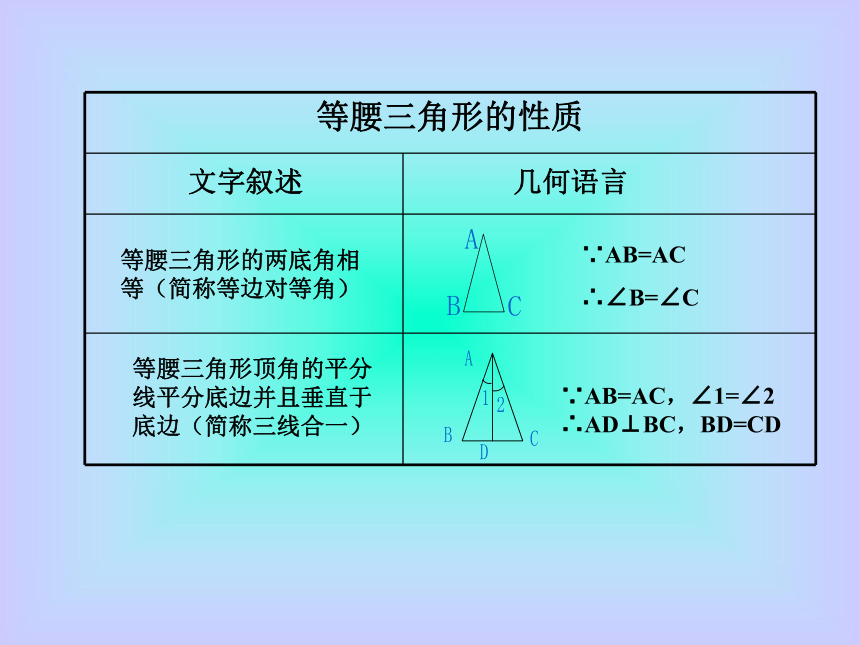
∴ BD=CD ,∠BAD=∠CAD (三线合一)文字叙述几何语言等腰三角形的两底角相等(简称等边对等角)∵AB=AC
∴∠B=∠C等腰三角形顶角的平分线平分底边并且垂直于底边(简称三线合一)∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD练习判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合。( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
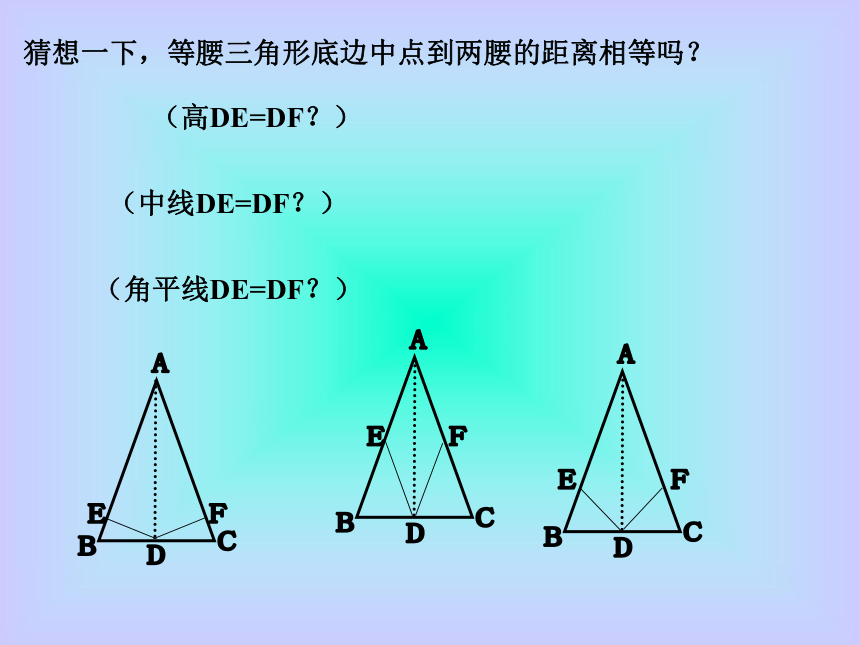
(4)钝角三角形不可能是等腰三角形 . ( )××作业猜想一下,等腰三角形底边中点到两腰的距离相等吗?(高DE=DF?)(中线DE=DF?)(角平线DE=DF?)题 型 探 究例1 已知:如图,房屋的顶角? BAC=100 ?,过屋顶A的立柱AD?BC,屋椽AB=AC.求顶架上?B, ?C,
?BAD, ?CAD
的度数。例2 已知线段a, h,用直尺和圆规作等腰三角形ABC,使底边BC=a, BC边上的高为h.ha作法:1.作线段BC=a.2.作BC的中垂线m,交BC于点D.3.在直线 m上截取DA=h,连接AB,AC.△ABC就是所求的等腰三角形.ABCD已知:△ABC中,AB=AC, AD=ED=EC.CD=BD求△ABC各角的度数。E例3ABCD已知:如图,AB=BC=CD=ED=EF.EFMN∠A=15°,你能求出哪些角的度数?例4例5已知:点D、E在△ABC中, AB=AC,AD=AE. 求证:BD=CE。ABCDE练习:1.△ABC是等边三角形,中线BD、CE相交于点O,则以点O为顶点的4个角的度数是2.已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC。 求证:AO⊥BCC小结1.等腰三角形的性质及其的应用。2.培养方程的思想。3.利用“三线合一”的一般辅助线。
(简写成 “等边对等角”) ∵AB=AC(已知)
∴∠B=∠C(等边对等角)复习2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.( 简写成“三线合一” )∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(三线合一)∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(三线合一)∵AB=AC, AD⊥BC (已知)
∴ BD=CD ,∠BAD=∠CAD (三线合一)文字叙述几何语言等腰三角形的两底角相等(简称等边对等角)∵AB=AC
∴∠B=∠C等腰三角形顶角的平分线平分底边并且垂直于底边(简称三线合一)∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD练习判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合。( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××作业猜想一下,等腰三角形底边中点到两腰的距离相等吗?(高DE=DF?)(中线DE=DF?)(角平线DE=DF?)题 型 探 究例1 已知:如图,房屋的顶角? BAC=100 ?,过屋顶A的立柱AD?BC,屋椽AB=AC.求顶架上?B, ?C,
?BAD, ?CAD
的度数。例2 已知线段a, h,用直尺和圆规作等腰三角形ABC,使底边BC=a, BC边上的高为h.ha作法:1.作线段BC=a.2.作BC的中垂线m,交BC于点D.3.在直线 m上截取DA=h,连接AB,AC.△ABC就是所求的等腰三角形.ABCD已知:△ABC中,AB=AC, AD=ED=EC.CD=BD求△ABC各角的度数。E例3ABCD已知:如图,AB=BC=CD=ED=EF.EFMN∠A=15°,你能求出哪些角的度数?例4例5已知:点D、E在△ABC中, AB=AC,AD=AE. 求证:BD=CE。ABCDE练习:1.△ABC是等边三角形,中线BD、CE相交于点O,则以点O为顶点的4个角的度数是2.已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC。 求证:AO⊥BCC小结1.等腰三角形的性质及其的应用。2.培养方程的思想。3.利用“三线合一”的一般辅助线。
