14.3 等腰三角形的判定[上学期]
文档属性
| 名称 | 14.3 等腰三角形的判定[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 188.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-17 16:50:00 | ||
图片预览




文档简介
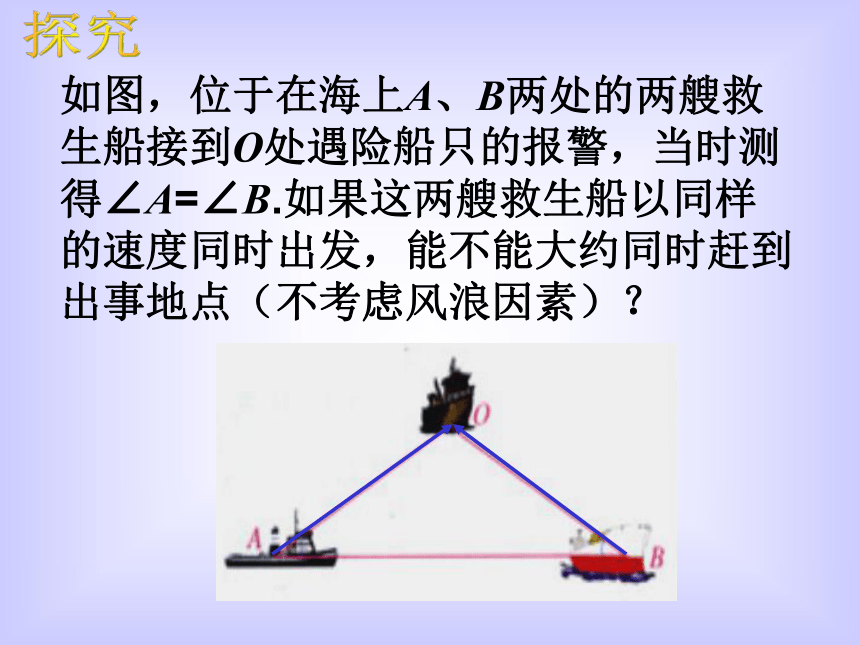
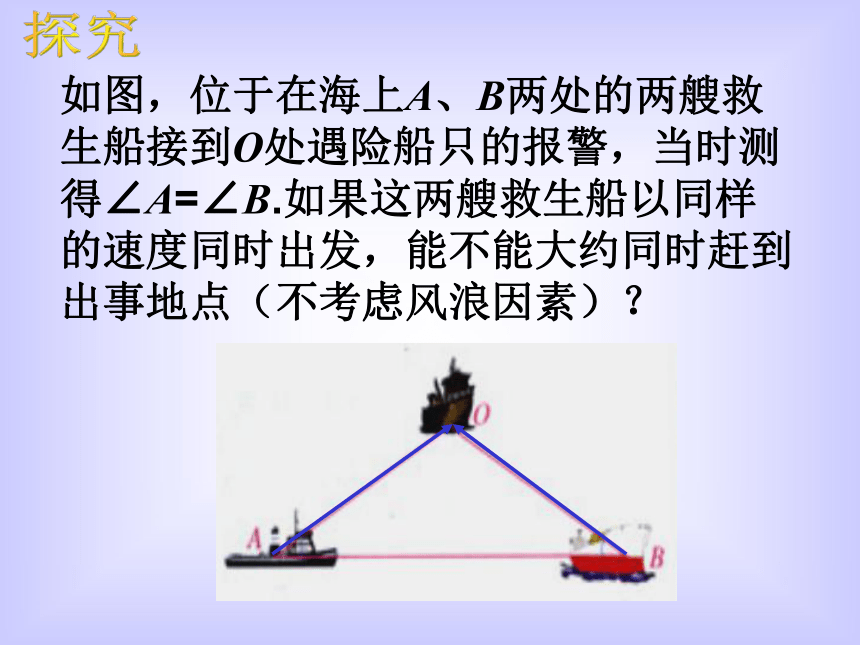
课件22张PPT。等腰三角形的判定如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?探究我们在上一节学习了等腰三角形的性质。现在你能回答我一些问题吗?
一、复习:1、等腰三角形的性质定理是什么?等腰三角形的两个底角相等。
(可以简称:等边对等角)2、这个定理的逆命题是什么?如果一个三角形有两个角相等,
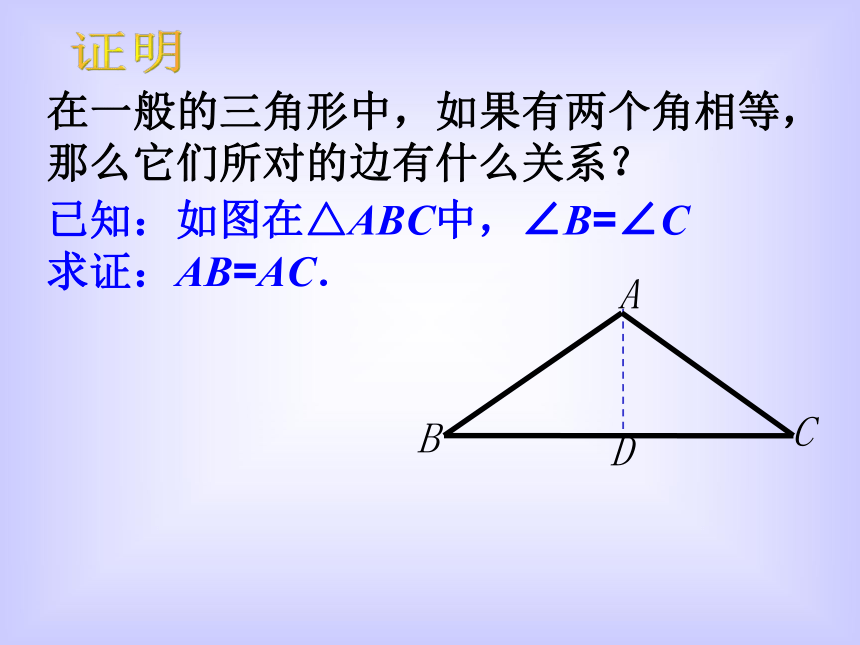
那么这个三角形是等腰三角形。3、这个命题正确吗?你能证明吗?在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?已知:如图在△ABC中,∠B=∠C
求证:AB=AC.证明等腰三角形的判定定理:
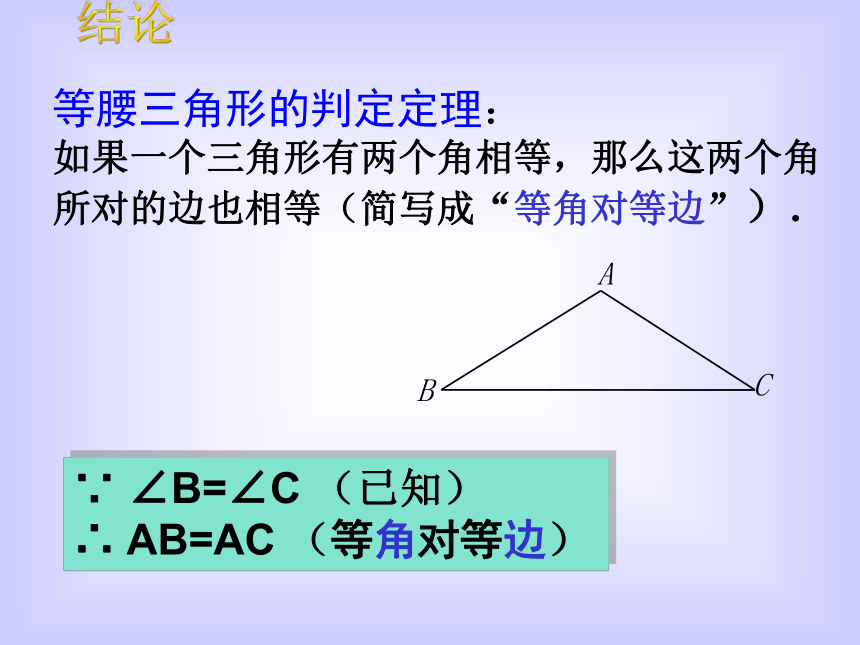
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”). 结论∵ ∠B=∠C (已知)
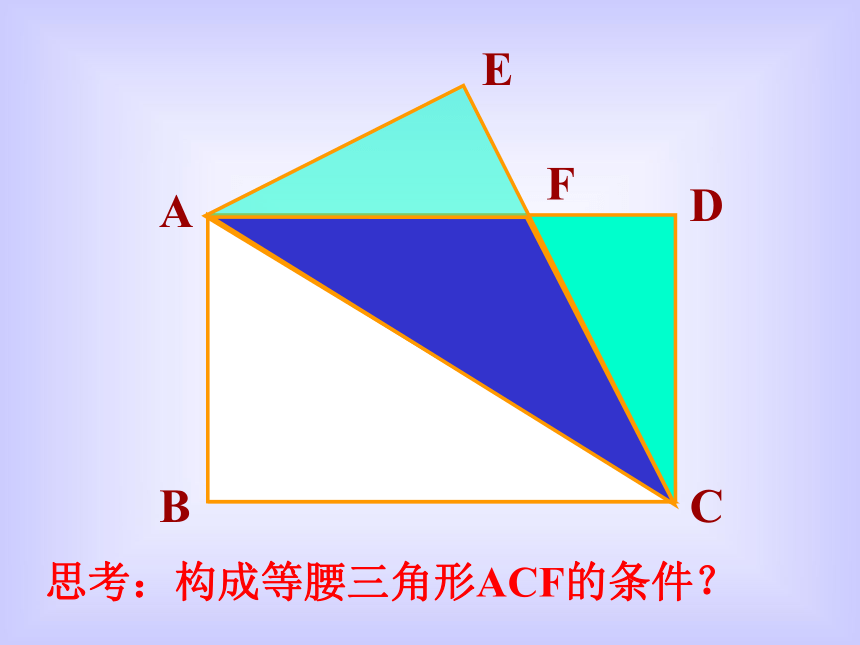
∴ AB=AC (等角对等边)如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?探究ABCDEF思考:构成等腰三角形ACF的条件?ABCEF已知:如图,AC平分∠ECB,AF//BC,△AFC是 。等腰三角形ABCEF已知:如图,AC平分∠ECB,△AFC是等腰三角形则 。AF//BCABCEF已知:如图, AF//BC ,△AFC是等腰三角形则 。AC平分∠ECBABCEF结论:在图中,平行线 ,等腰三角形,角平分线,其中有两条成立,第三条一定成立 。题型探究如图,AD∥BC,BD平分∠ABC。
求证:AB=AD。ADBC已知:∠CAE是△ABC的外角,∠1=∠2,AD//BC。求证:AB=AC例1求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。已知:∠CAE是△ABC的外角,AD//BC, AB=AC 。你能得出什么结论?∠1=∠2已知:∠CAE是△ABC的外角,。∠1=∠2 ,AB=ACAD//BC你能得出什么结论?已知:如图,△ABC中,AB=AC,BD、CE是两条角平分线,并且BD、CE交于点O。例4:求证:等腰三角形两底角的平分线的交点到底边的两端点距离相等。求证:OB=OC已知:如图,△ABC中,AB=AC,∠ABC与∠ACB的平分线相交于点O。你能得出什么结论?ACBO变式:OA已知:如图,△ABC中,∠ABC与∠ACB的平分线相交于点O。你能得出什么结论?变式:小结1、等腰三角形的性质定理。2、等腰三角形的判定定理。
一、复习:1、等腰三角形的性质定理是什么?等腰三角形的两个底角相等。
(可以简称:等边对等角)2、这个定理的逆命题是什么?如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。3、这个命题正确吗?你能证明吗?在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?已知:如图在△ABC中,∠B=∠C
求证:AB=AC.证明等腰三角形的判定定理:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”). 结论∵ ∠B=∠C (已知)
∴ AB=AC (等角对等边)如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?探究ABCDEF思考:构成等腰三角形ACF的条件?ABCEF已知:如图,AC平分∠ECB,AF//BC,△AFC是 。等腰三角形ABCEF已知:如图,AC平分∠ECB,△AFC是等腰三角形则 。AF//BCABCEF已知:如图, AF//BC ,△AFC是等腰三角形则 。AC平分∠ECBABCEF结论:在图中,平行线 ,等腰三角形,角平分线,其中有两条成立,第三条一定成立 。题型探究如图,AD∥BC,BD平分∠ABC。
求证:AB=AD。ADBC已知:∠CAE是△ABC的外角,∠1=∠2,AD//BC。求证:AB=AC例1求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。已知:∠CAE是△ABC的外角,AD//BC, AB=AC 。你能得出什么结论?∠1=∠2已知:∠CAE是△ABC的外角,。∠1=∠2 ,AB=ACAD//BC你能得出什么结论?已知:如图,△ABC中,AB=AC,BD、CE是两条角平分线,并且BD、CE交于点O。例4:求证:等腰三角形两底角的平分线的交点到底边的两端点距离相等。求证:OB=OC已知:如图,△ABC中,AB=AC,∠ABC与∠ACB的平分线相交于点O。你能得出什么结论?ACBO变式:OA已知:如图,△ABC中,∠ABC与∠ACB的平分线相交于点O。你能得出什么结论?变式:小结1、等腰三角形的性质定理。2、等腰三角形的判定定理。
