等腰三角形[上学期]
图片预览



文档简介
课件13张PPT。等腰三角形的性质广元市利州中学
周 思 波复习已知:∠A(如右图)
求作:射线AD,使
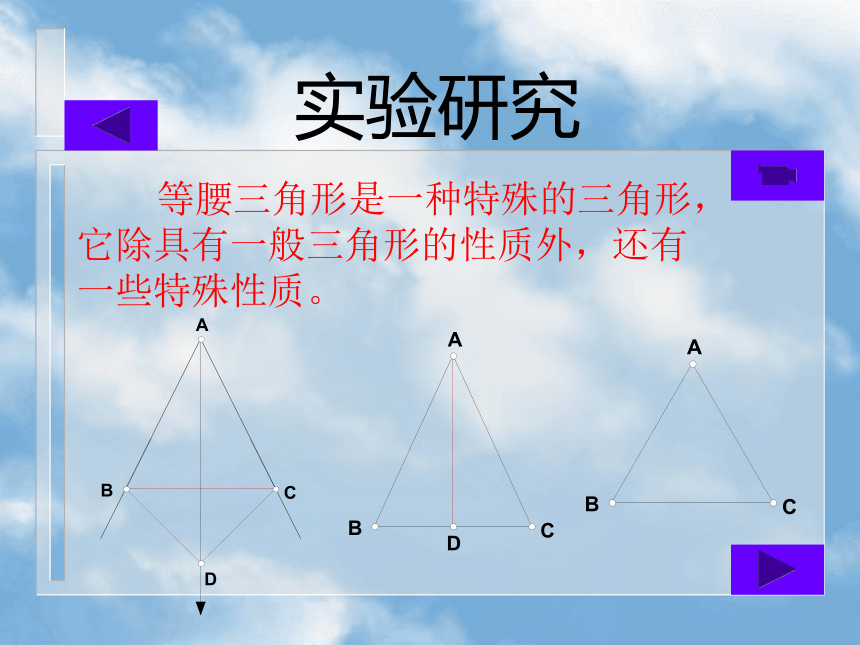
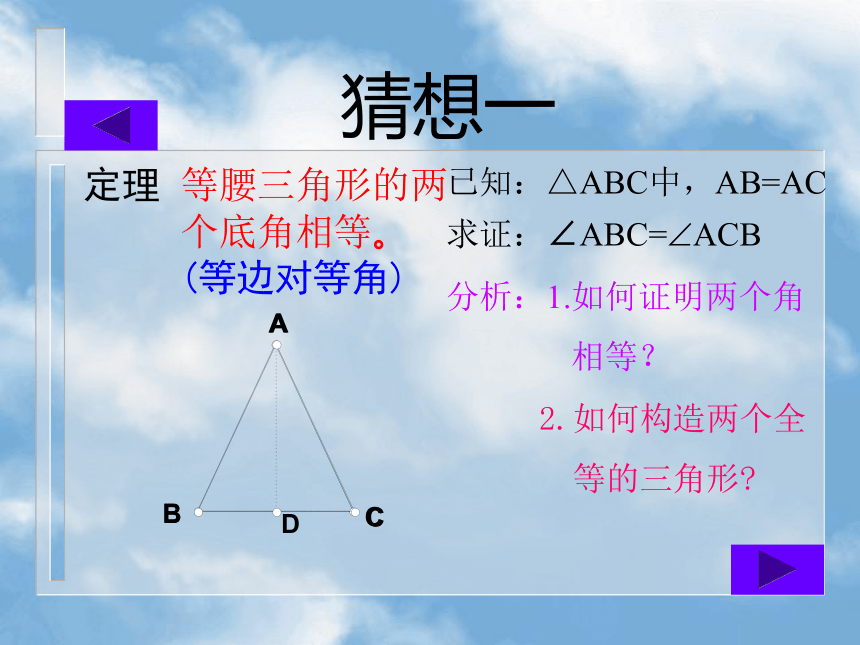
AD平分∠A.基本作图:平分已知角实验研究 等腰三角形是一种特殊的三角形,它除具有一般三角形的性质外,还有一些特殊性质。猜想一等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠ABC=?ACB分析:1.如何证明两个角
相等? 2.如何构造两个全
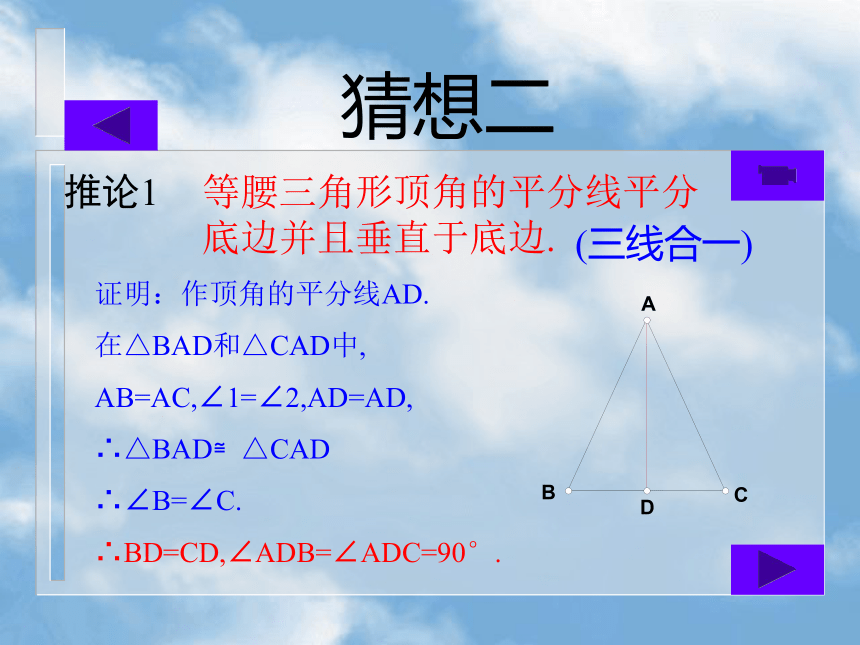
等的三角形?定理(等边对等角)猜想二等腰三角形顶角的平分线平分底边并且垂直于底边.证明:作顶角的平分线AD.
在△BAD和△CAD中,
AB=AC,∠1=∠2,AD=AD,
∴△BAD≌△CAD
∴∠B=∠C.∴BD=CD,∠ADB=∠ADC=90°.推论1(三线合一)猜想三证明: ∵AB=AC(已知)等边三角形的各角都相等,并且每一个角都等于60°.推论2已知:△ABC中,AB=AC=BC.求证:∠A=∠B=∠C=60°∴∠B=∠C(等边对等角)∵AB=BC(已知)∴∠A=∠C(等边对等角)又∵∠A+∠B+∠C=180°(三角形内角和定理)∴∠A=∠B =∠C=60°⒈等腰三角形一个底角为75°,它的另外两个角为_______
⒉等腰三角形一个角为70°,它的另外两个角为
___________________
⒊等腰三角形一个角为110°,它的另外两个角为________ 结论:在等腰三角形中,
① 顶角+2×底角=180°
② 顶角=180°-2×底角④0°<顶角<180°
⑤0°<底角<90°75°,30°70°,40°或55°,55°35°,35°巩固练习一③ 底角=(180°-顶角)÷2巩固练习二(1)∵AD⊥BC,
∴∠____ = ∠____,___= ___ (2)∵AD是中线,
∴___⊥___ ,∠____ =∠____(3)∵AD是角平分线,
∴___ ⊥___ ,___ =___BAD CADBD CD AD BC AD BCBAD CADBD CD 根据等腰三角形性质定理的推论,在△ABC中, AB=AC时, 例题巩固练习三⑴找出下面图形中相等的角:(1)在△ABC中,AC=BC, ∠ACB=90°,CD⊥AB
∠A=∠B=∠ACD=∠BCD=45°∠ADC=∠BDC=∠ACB=90°(2)在△ABC中,AC=BC=AC,AD是高
找出下面图形中相等的角:∠A=∠B=∠BAC=60°巩固练习三⑵∠BAD=∠CAD=30° ∠ADC=∠ADB=90°例题一 已知:如图,房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC, 求顶架上∠B、∠C、∠BAD、∠CAD的度数。解:在△ABC中,∵AB=AC(已知)∴∠B=∠C(等边对等角)∴∠B=∠C= (180°-∠A)=40°(三角形内角和定理)又∵AD⊥BC(已知)∴∠BAD=∠CAD(等腰三角形顶角的平分线与底边上的高互相重合)∴∠BAD=∠CAD=50°关于撑伞的数学问题已知:如图,AB=AC,DB=DC问:AD与BC有什么关系?猜想:AD垂直平分BC证明:
∵AB=AC,BD=CD,AD=CD∴△ABD≌△ACD(SSS)∴∠BAD=∠CAD∴AD垂直平分BC小结角平分线等腰三角形性质等腰三角形三线合一等边对等角等边三角形各边都相等作业:习题3.6第2、3、4题
周 思 波复习已知:∠A(如右图)
求作:射线AD,使
AD平分∠A.基本作图:平分已知角实验研究 等腰三角形是一种特殊的三角形,它除具有一般三角形的性质外,还有一些特殊性质。猜想一等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠ABC=?ACB分析:1.如何证明两个角
相等? 2.如何构造两个全
等的三角形?定理(等边对等角)猜想二等腰三角形顶角的平分线平分底边并且垂直于底边.证明:作顶角的平分线AD.
在△BAD和△CAD中,
AB=AC,∠1=∠2,AD=AD,
∴△BAD≌△CAD
∴∠B=∠C.∴BD=CD,∠ADB=∠ADC=90°.推论1(三线合一)猜想三证明: ∵AB=AC(已知)等边三角形的各角都相等,并且每一个角都等于60°.推论2已知:△ABC中,AB=AC=BC.求证:∠A=∠B=∠C=60°∴∠B=∠C(等边对等角)∵AB=BC(已知)∴∠A=∠C(等边对等角)又∵∠A+∠B+∠C=180°(三角形内角和定理)∴∠A=∠B =∠C=60°⒈等腰三角形一个底角为75°,它的另外两个角为_______
⒉等腰三角形一个角为70°,它的另外两个角为
___________________
⒊等腰三角形一个角为110°,它的另外两个角为________ 结论:在等腰三角形中,
① 顶角+2×底角=180°
② 顶角=180°-2×底角④0°<顶角<180°
⑤0°<底角<90°75°,30°70°,40°或55°,55°35°,35°巩固练习一③ 底角=(180°-顶角)÷2巩固练习二(1)∵AD⊥BC,
∴∠____ = ∠____,___= ___ (2)∵AD是中线,
∴___⊥___ ,∠____ =∠____(3)∵AD是角平分线,
∴___ ⊥___ ,___ =___BAD CADBD CD AD BC AD BCBAD CADBD CD 根据等腰三角形性质定理的推论,在△ABC中, AB=AC时, 例题巩固练习三⑴找出下面图形中相等的角:(1)在△ABC中,AC=BC, ∠ACB=90°,CD⊥AB
∠A=∠B=∠ACD=∠BCD=45°∠ADC=∠BDC=∠ACB=90°(2)在△ABC中,AC=BC=AC,AD是高
找出下面图形中相等的角:∠A=∠B=∠BAC=60°巩固练习三⑵∠BAD=∠CAD=30° ∠ADC=∠ADB=90°例题一 已知:如图,房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC, 求顶架上∠B、∠C、∠BAD、∠CAD的度数。解:在△ABC中,∵AB=AC(已知)∴∠B=∠C(等边对等角)∴∠B=∠C= (180°-∠A)=40°(三角形内角和定理)又∵AD⊥BC(已知)∴∠BAD=∠CAD(等腰三角形顶角的平分线与底边上的高互相重合)∴∠BAD=∠CAD=50°关于撑伞的数学问题已知:如图,AB=AC,DB=DC问:AD与BC有什么关系?猜想:AD垂直平分BC证明:
∵AB=AC,BD=CD,AD=CD∴△ABD≌△ACD(SSS)∴∠BAD=∠CAD∴AD垂直平分BC小结角平分线等腰三角形性质等腰三角形三线合一等边对等角等边三角形各边都相等作业:习题3.6第2、3、4题
