2022-2023学年高一数学人教B版(2019)必修第一册课件:1.1.3 集合的基本运算(共20张PPT)
文档属性
| 名称 | 2022-2023学年高一数学人教B版(2019)必修第一册课件:1.1.3 集合的基本运算(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-21 09:01:28 | ||
图片预览






文档简介
(共20张PPT)
第一章 集合与常用逻辑用语
1.1 集合
1.1.3 集合的基本运算
教学目标:
1.理解两个集合的交集、并集的含义,会求两个集合的交集和并集.
2.理解补集的含义,会求给定子集的补集.
3.能借助Venn图表达集合之间的关系.
重点:
交集与并集、全集与补集的概念.
难点:
理解交集与并集的概念,以及符号之间的区别与联系.
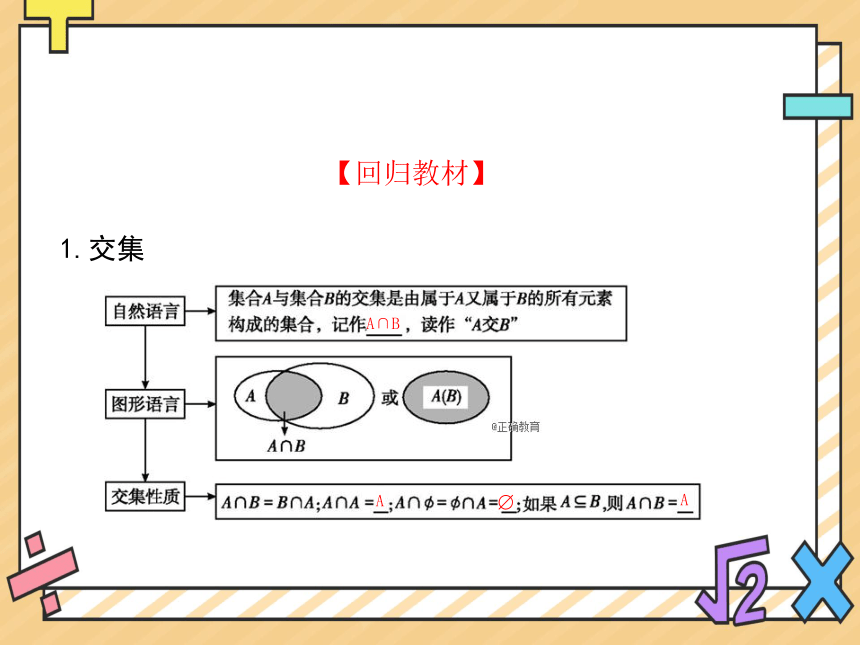
【回归教材】
A∩B
A
A
1.交集
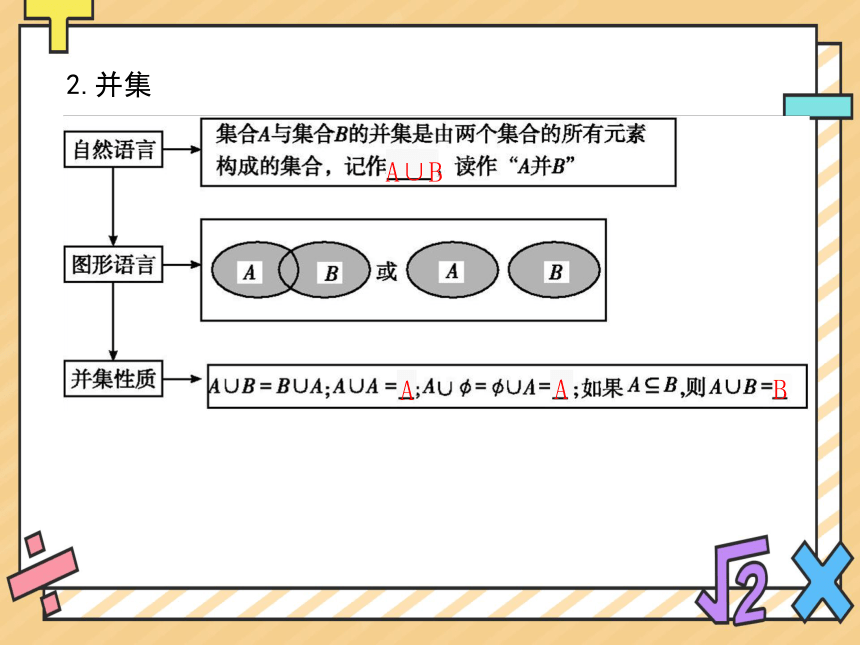
2.并集
A∪B
A
A
B
3.补集
不属于
A在U中的补集
U
A
A
A
A
=
=
U
A
1.设全集U={1,2,3,4,5},集合M={1,4},N={1,3,5},则N∩( UM)等于( )
(A){1,3} (B){1,5}
(C){4,5} (D){3,5}
【做一做】
【答案】D
全集U={1,2,3,4,5},集合M={1,4},
UM={2,3,5},N={1,3,5}
所以N∩( UM)={3,5}.故选D.
2.集合M={-1,1,3,5},集合N={-3,1,5},则以下选项正确的是( )
(A)N∈M (B)N M
(C)N∩M={1,5} (D)N∪M={-3,-1,3}
【答案】D
解析:因为1,5既是集合M={-1,1,3,5}中的元素,又是集合N={-3,1,5}中的元素,且两集合没有其他公共元素,所以N∩M={1,5},故选C.
【例1】(1)已知全集U={1,2,3,4,5,6,7},集合A={1,3,5,6},则 UA等于( )
(A){1,3,5,6} (B){2,3,7}
(C){2,4,7} (D){2,5,7}
(2)设全集U=R,集合A={x|x<-1或x≥2},集合B={x|0求交集、并集、补集
【知识点1】
(1)由题意知 UA={2,4,7}.故选C.
(2)画出数轴,标出集合A,
如图(1)所示.
则 RA={x|-1≤x<2},再将集合 RA与B画在同一数轴上,如图(2)所示.
所以( RA)∪B={x|-1≤x≤3}.
答案:(1)C (2){x|-1≤x≤3}
求交集、并集、补集
【知识点1】
【方法规律】用列举法表示的数集在求集合运算时,可直接通过观察写出满足题意的集合运算;用描述法表示的数集在求集合运算时,如果集合是无限集,且直接观察不出或不易得出运算结果,则应把两个集合在数轴上表示出来,根据集合运算的定义写出结果.
【变式训练】
若集合A={x|-2≤x≤3},B={x|x<-1或x>4},则集合A∩B等于( )
(A){x|x≤3,或x>4} (B){x|-1(C){x|3≤x<4} (D){x|-2≤x<-1}
解析:在数轴上标出A,B所表示的集合,如图所示,取其公共部分即得A∩B={x|-2≤x<-1},故选D.
【例2】已知集合S={x|x>5或x<-1},集合T={x|a已知集合求参数的运算问题
【知识点2】
解析:S={x|x>5或x<-1},T={x|a所以a的取值范围为
【例3】已知全集U={不大于20的质数},M,N是U的两个子集,且满足M∩( UN)={3,5},
( UM)∩N={7,19},( UM)∩( UN)={2,17},求M,N.
Venn图在集合运算中的应用
【知识点3】
解析:由已知得U={2,3,5,7,11,13,17,19},根据题意画出Venn图,
如图所示,可得M={3,5,11,13},N={7,11,13,19}.
1.设集合U={1,2,3,4,5,6}, A={1,3,5},B={3,4,5},则 (A∪B)= ( )
A.{2,6} B.{3,6}
C.{1,3,4,5} D.{1,2,4,6}
【答案】A
【解析】A∪B={1,3,4,5},
所以 (A∪B)={2,6}.
【练一练】
2.已知全集U={1,2,3,4},集合A={1,2},B={2,3},则( A)∪B= ( )
A.{2} B.{3} C.{2,3} D.{2,3,4}
【答案】D
【解析】依题意, A={3,4},则( A)∪B={2,3,4}.
第一章 集合与常用逻辑用语
1.1 集合
1.1.3 集合的基本运算
教学目标:
1.理解两个集合的交集、并集的含义,会求两个集合的交集和并集.
2.理解补集的含义,会求给定子集的补集.
3.能借助Venn图表达集合之间的关系.
重点:
交集与并集、全集与补集的概念.
难点:
理解交集与并集的概念,以及符号之间的区别与联系.
【回归教材】
A∩B
A
A
1.交集
2.并集
A∪B
A
A
B
3.补集
不属于
A在U中的补集
U
A
A
A
A
=
=
U
A
1.设全集U={1,2,3,4,5},集合M={1,4},N={1,3,5},则N∩( UM)等于( )
(A){1,3} (B){1,5}
(C){4,5} (D){3,5}
【做一做】
【答案】D
全集U={1,2,3,4,5},集合M={1,4},
UM={2,3,5},N={1,3,5}
所以N∩( UM)={3,5}.故选D.
2.集合M={-1,1,3,5},集合N={-3,1,5},则以下选项正确的是( )
(A)N∈M (B)N M
(C)N∩M={1,5} (D)N∪M={-3,-1,3}
【答案】D
解析:因为1,5既是集合M={-1,1,3,5}中的元素,又是集合N={-3,1,5}中的元素,且两集合没有其他公共元素,所以N∩M={1,5},故选C.
【例1】(1)已知全集U={1,2,3,4,5,6,7},集合A={1,3,5,6},则 UA等于( )
(A){1,3,5,6} (B){2,3,7}
(C){2,4,7} (D){2,5,7}
(2)设全集U=R,集合A={x|x<-1或x≥2},集合B={x|0
【知识点1】
(1)由题意知 UA={2,4,7}.故选C.
(2)画出数轴,标出集合A,
如图(1)所示.
则 RA={x|-1≤x<2},再将集合 RA与B画在同一数轴上,如图(2)所示.
所以( RA)∪B={x|-1≤x≤3}.
答案:(1)C (2){x|-1≤x≤3}
求交集、并集、补集
【知识点1】
【方法规律】用列举法表示的数集在求集合运算时,可直接通过观察写出满足题意的集合运算;用描述法表示的数集在求集合运算时,如果集合是无限集,且直接观察不出或不易得出运算结果,则应把两个集合在数轴上表示出来,根据集合运算的定义写出结果.
【变式训练】
若集合A={x|-2≤x≤3},B={x|x<-1或x>4},则集合A∩B等于( )
(A){x|x≤3,或x>4} (B){x|-1
解析:在数轴上标出A,B所表示的集合,如图所示,取其公共部分即得A∩B={x|-2≤x<-1},故选D.
【例2】已知集合S={x|x>5或x<-1},集合T={x|a
【知识点2】
解析:S={x|x>5或x<-1},T={x|a
【例3】已知全集U={不大于20的质数},M,N是U的两个子集,且满足M∩( UN)={3,5},
( UM)∩N={7,19},( UM)∩( UN)={2,17},求M,N.
Venn图在集合运算中的应用
【知识点3】
解析:由已知得U={2,3,5,7,11,13,17,19},根据题意画出Venn图,
如图所示,可得M={3,5,11,13},N={7,11,13,19}.
1.设集合U={1,2,3,4,5,6}, A={1,3,5},B={3,4,5},则 (A∪B)= ( )
A.{2,6} B.{3,6}
C.{1,3,4,5} D.{1,2,4,6}
【答案】A
【解析】A∪B={1,3,4,5},
所以 (A∪B)={2,6}.
【练一练】
2.已知全集U={1,2,3,4},集合A={1,2},B={2,3},则( A)∪B= ( )
A.{2} B.{3} C.{2,3} D.{2,3,4}
【答案】D
【解析】依题意, A={3,4},则( A)∪B={2,3,4}.
