等腰三角形性质[上学期]
文档属性
| 名称 | 等腰三角形性质[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 952.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-29 00:00:00 | ||
图片预览







文档简介
课件23张PPT。等腰三角形怀化三中数学组王红剑生活中的三角形学习目标: 1、了解等腰三角形的有关概念。
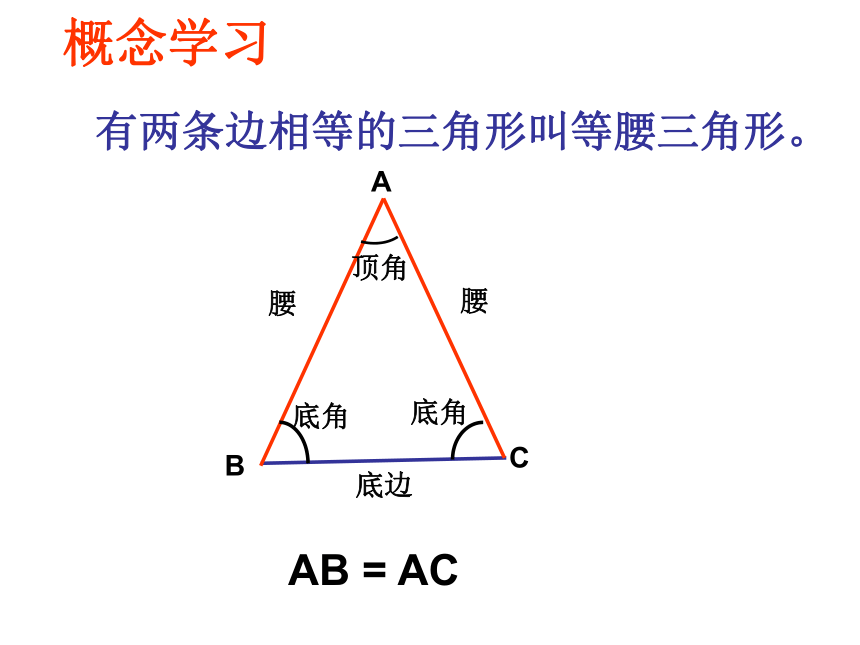
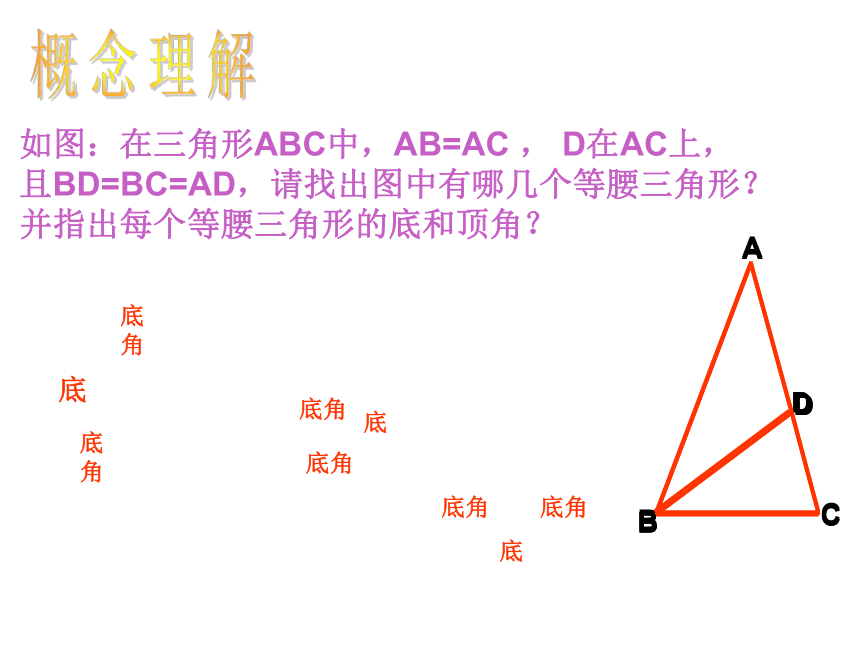
2、掌握等腰三角形的性质。等腰三角形概念学习有两条边相等的三角形叫等腰三角形。ABC腰腰底边底角底角顶角AB = AC如图:在三角形ABC中,AB=AC , D在AC上,且BD=BC=AD,请找出图中有哪几个等腰三角形?并指出每个等腰三角形的底和顶角?概念理解ACDB问题探索1
1、等腰三角形ABC是___对
称图形,折痕AD所在的直线是它的_________。2、∠B 与 ∠ ___重合,
因此∠B = ∠ ___等腰三角形的两个___ 角相等。
∵ AB = AC
∴ ∠B = ∠C操作:结论:应用:将等腰三角形ABC沿AD对折:轴对称轴CC底ABCD演 示下一页返 回思考:等腰三角形的底角可以是直角或钝角吗?为什么?(不能,因为等腰三角形两底角相等,若底角是直角或钝角,三角形的内角和大于180°)问题探索2操作: 画等腰三角形ABC顶角的平分线、底边的高和底边的中线。ACB结论: 等腰三角形顶角的平分线、底边的高和底边的中线互相____。重合(简称“三线合一”)
1、∵ AB=AC, AD⊥BC,
∴ ∠ =∠ , = 。
2、∵ AB=AC, AD是中线
∴ ⊥ , ∠ = ∠ .
3、∵ AB=AC, AD是角平分线
∴ ⊥ , = 。BADCADBDCDBADADBCCADADBCBDCD应用:演 示下一页┓顶角的平分线底边的高底边的中线返 回例题讲解例:已知:在等腰△ABC中, ,∠B=800,
求∠ C 和 ∠A的度数?
1、 AB=AC表示AB和AC是三角形的___,
底角是∠___和∠___。
2、先应根据__________, 求出∠___。
3、再根据 _____________, 求出∠___。腰等边对等角C三角形的内角和ABC 画图、讨论:解:∵AB=AC
∴ ∠C= ∠B=800
∵ ∠A+ ∠B+ ∠C=1800
∴ ∠A=1800- 800- 800=200AB=AC例:已知:在等腰△ABC中,∠B=800,
求:∠ C 和 ∠A的度数?例题变式(图一)讨论:∠B的位置有几种可能?
(可能是底角或顶角)分析:当∠B为底角时, ∠C为800,
∠A为200;当∠B为顶角时, ∠C为500,
∠A为500。题组训练题组1: ①如果等腰三角形的一个底角为500,
则其余两个角为____和___。②如果等腰三角形的顶角为800,
则它的一个底角为___。500800500题组训练题组2:1、等腰三角形的一个内角为1200,则另两角为_________。2、等腰三角形的一个外角为1300,则三个内角分别为:_______________________________。3、等腰三角形的一个内角是另一个内角的2倍,则三
个内角分别为:_______________________________。
分析:设小角为α,则大角为2α.当α为底角时, α +α+ 2α=1800
解得 α=450,则2α=900当2α为底角时, α +2α+ 2α=1800
解得α =360,则2α=720∴其内角的度数为450,450,900,或360,720,720.300和300650、650、500或500、500、800450、450、900或360、720、720如图:在三角形ABC中,AB=AC , D在 AC上,且BD=BC=AD,求△ABC各内角的度数?问题解析讨论:2、∠A与哪些角相等?1、∠C与哪些角相等?(∠3、 ∠ABC )123( ∠1、 ∠2 )3、 ∠C与∠A是什么关系?( ∠C=2 ∠A )解:∵BD=AD, ∴ ∠1= ∠A∵ ∠3= ∠1+ ∠A, ∴ ∠3=2 ∠A∵ BD=BC, ∴ ∠3= ∠C, ∴ ∠C=2 ∠A∵ AB=AC, ∴ ∠ABC= ∠C=2 ∠A∵ ∠A+ ∠ABC+ ∠C=1800, ∴ 5 ∠A=1800,
∴ ∠A=360, ∴ ∠ABC= ∠C=2 ∠A=720课堂小结等腰三角形概念性质等边对等角三线合一有两边相等的三角形腰、底、顶角、底角作业1、P86:2、3、4。
2、寻找生活中的等腰三角形。
2、掌握等腰三角形的性质。等腰三角形概念学习有两条边相等的三角形叫等腰三角形。ABC腰腰底边底角底角顶角AB = AC如图:在三角形ABC中,AB=AC , D在AC上,且BD=BC=AD,请找出图中有哪几个等腰三角形?并指出每个等腰三角形的底和顶角?概念理解ACDB问题探索1
1、等腰三角形ABC是___对
称图形,折痕AD所在的直线是它的_________。2、∠B 与 ∠ ___重合,
因此∠B = ∠ ___等腰三角形的两个___ 角相等。
∵ AB = AC
∴ ∠B = ∠C操作:结论:应用:将等腰三角形ABC沿AD对折:轴对称轴CC底ABCD演 示下一页返 回思考:等腰三角形的底角可以是直角或钝角吗?为什么?(不能,因为等腰三角形两底角相等,若底角是直角或钝角,三角形的内角和大于180°)问题探索2操作: 画等腰三角形ABC顶角的平分线、底边的高和底边的中线。ACB结论: 等腰三角形顶角的平分线、底边的高和底边的中线互相____。重合(简称“三线合一”)
1、∵ AB=AC, AD⊥BC,
∴ ∠ =∠ , = 。
2、∵ AB=AC, AD是中线
∴ ⊥ , ∠ = ∠ .
3、∵ AB=AC, AD是角平分线
∴ ⊥ , = 。BADCADBDCDBADADBCCADADBCBDCD应用:演 示下一页┓顶角的平分线底边的高底边的中线返 回例题讲解例:已知:在等腰△ABC中, ,∠B=800,
求∠ C 和 ∠A的度数?
1、 AB=AC表示AB和AC是三角形的___,
底角是∠___和∠___。
2、先应根据__________, 求出∠___。
3、再根据 _____________, 求出∠___。腰等边对等角C三角形的内角和ABC 画图、讨论:解:∵AB=AC
∴ ∠C= ∠B=800
∵ ∠A+ ∠B+ ∠C=1800
∴ ∠A=1800- 800- 800=200AB=AC例:已知:在等腰△ABC中,∠B=800,
求:∠ C 和 ∠A的度数?例题变式(图一)讨论:∠B的位置有几种可能?
(可能是底角或顶角)分析:当∠B为底角时, ∠C为800,
∠A为200;当∠B为顶角时, ∠C为500,
∠A为500。题组训练题组1: ①如果等腰三角形的一个底角为500,
则其余两个角为____和___。②如果等腰三角形的顶角为800,
则它的一个底角为___。500800500题组训练题组2:1、等腰三角形的一个内角为1200,则另两角为_________。2、等腰三角形的一个外角为1300,则三个内角分别为:_______________________________。3、等腰三角形的一个内角是另一个内角的2倍,则三
个内角分别为:_______________________________。
分析:设小角为α,则大角为2α.当α为底角时, α +α+ 2α=1800
解得 α=450,则2α=900当2α为底角时, α +2α+ 2α=1800
解得α =360,则2α=720∴其内角的度数为450,450,900,或360,720,720.300和300650、650、500或500、500、800450、450、900或360、720、720如图:在三角形ABC中,AB=AC , D在 AC上,且BD=BC=AD,求△ABC各内角的度数?问题解析讨论:2、∠A与哪些角相等?1、∠C与哪些角相等?(∠3、 ∠ABC )123( ∠1、 ∠2 )3、 ∠C与∠A是什么关系?( ∠C=2 ∠A )解:∵BD=AD, ∴ ∠1= ∠A∵ ∠3= ∠1+ ∠A, ∴ ∠3=2 ∠A∵ BD=BC, ∴ ∠3= ∠C, ∴ ∠C=2 ∠A∵ AB=AC, ∴ ∠ABC= ∠C=2 ∠A∵ ∠A+ ∠ABC+ ∠C=1800, ∴ 5 ∠A=1800,
∴ ∠A=360, ∴ ∠ABC= ∠C=2 ∠A=720课堂小结等腰三角形概念性质等边对等角三线合一有两边相等的三角形腰、底、顶角、底角作业1、P86:2、3、4。
2、寻找生活中的等腰三角形。
