第6章 幂函数、指数函数和对数函数专项训练-2022-2023学年高一上学期数学苏教版(2019)必修第一册(含答案)
文档属性
| 名称 | 第6章 幂函数、指数函数和对数函数专项训练-2022-2023学年高一上学期数学苏教版(2019)必修第一册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 54.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-21 00:00:00 | ||
图片预览


文档简介
《第6章 幂函数、指数函数和对数函数》专项训练
专项一 与指数函数有关的复合函数问题
类型1 形如f(x)=(a>0,a≠1)的函数
1.若函数f(x)=3(2a-1)x+3在R上是减函数,则实数a的取值范围是( )
A.(-∞,) B.(,+∞)
C.(,1)∪(1,+∞) D.(,1)
2.(多选)[2022安徽蚌埠高一上期中]已知函数f(x)=(,则( )
A.f(x)的定义域为R
B.f(x)的值域为(0,2]
C.f(x)在[-2,+∞)上单调递增
D.f(x)在[-2,+∞)上单调递减
3. 已知函数f(x)=(a>0,a≠1).
(1)若a=2,解关于m的不等式f(m)-f(1-2m)≤0;
(2)若函数f(x)在区间(2,3)上单调递增,求实数a的取值范围.
类型2 形如f(x)=A(ax)2+B·ax+C(a>0,a≠1)的函数
4.若函数f(x)=ax(ax-3a2-1)(a>0,a≠1)在区间[0,+∞)上是增函数,则实数a的取值范围是( )
A.(0,] B.[,1)
C.(1,] D.[,+∞)
5.若不等式(m2-m)2x-()x<1对任意x∈(-∞,-1]恒成立,则实数m的取值范围是 .
6.[2022山东枣庄三中高一期中]已知函数f(x)=4x-λ·2x+1+3,x∈[-1,2].
(1)若λ=,求f(x)的值域;
(2)若函数f(x)的最小值为1,求实数λ的值.
类型3 形如f(x)=A(a2x+a-2x)+B(ax±a-x)+C(a>0,a≠1)的函数
7.[2022江苏南通高一上调研]已知函数f(x),g(x)分别是定义在R上的偶函数与奇函数,且f(x)+2g(x)=2x.
(1)求f(x)与g(x)的解析式;
(2)若 x∈(1,2),不等式f(2x)-(m+2)g(x)+2≥0恒成立,求实数m的最大值.
专项二 与对数函数有关的复合函数问题
类型1 形如f(x)=loga(Ax2+Bx+C)(a>0且a≠1)的函数
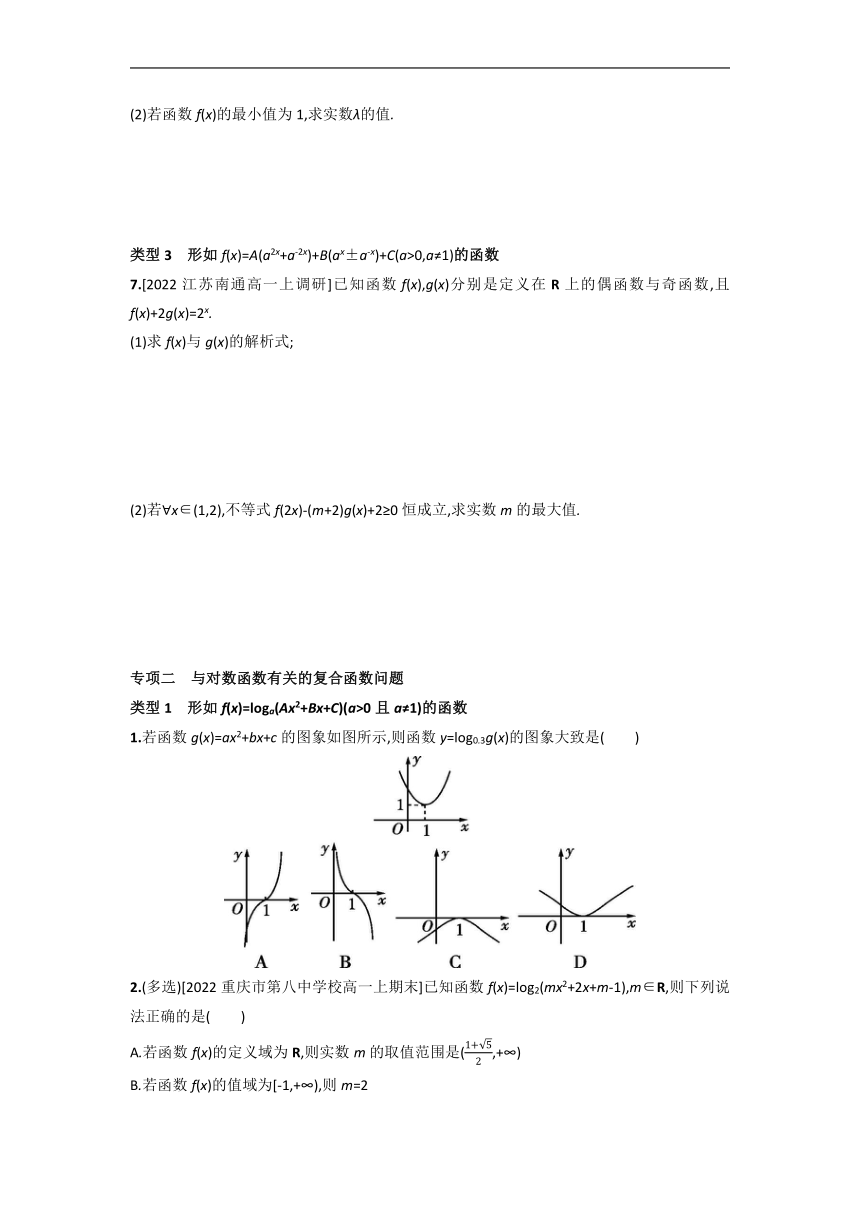
1.若函数g(x)=ax2+bx+c的图象如图所示,则函数y=log0.3g(x)的图象大致是( )
2.(多选)[2022重庆市第八中学校高一上期末]已知函数f(x)=log2(mx2+2x+m-1),m∈R,则下列说法正确的是( )
A.若函数f(x)的定义域为R,则实数m的取值范围是(,+∞)
B.若函数f(x)的值域为[-1,+∞),则m=2
C.若函数f(x)在[2,+∞)上为增函数,则实数m的取值范围是[0,+∞)
D.若m=0,则不等式f(x)<1的解集为(-∞,)
3.[2022黑龙江哈六中高一上期末]已知函数f(x)=loga(kx2-2x+6)(a>0且a≠1).
(1)若函数f(x)在[2,3]上恒有意义,求实数k的取值范围.
(2)是否存在实数k,使得函数f(x)在[2,3]上为增函数,且最大值为2 若存在,求出k的值;若不存在,请说明理由.
类型2 形如f(x)=A(logax)2+B·logax+C(a>0且a≠1)的函数
4.函数f(x)=(lg x)2-2lg x2+3(1≤x≤1 000)的值域为( )
A.[-1,0] B.[0,3]
C.[-1,3] D.[-1,+∞)
5.[2022重庆巴蜀中学高一上期中]设y=(log2x)2+(t-2)log2x-t+1,若t在[-2,2]上变化时,y恒取正值,则x的取值范围是 .
6.已知函数f(x)=(2log4x-2)(log4x+).
(1)当x∈[1,16]时,求该函数的值域;
(2)求不等式f(x)>2的解集;
(3)若存在x∈[4,16],使得不等式f(x)参考答案
专项一 与指数函数有关的复合函数问题
1.A 因为底数3∈(1,+∞),所以函数f(x)=3(2a-1)x+3的单调性与y=(2a-1)x+3的单调性相同.因为函数f(x)=3(2a-1)x+3在R上是减函数,所以y=(2a-1)x+3在R上是减函数,所以2a-1<0,即a<,即实数a的取值范围是(-∞,),选A.
2.ABD
3.(1)当a=2时,f(x)=.
f(m)-f(1-2m)≤0等价于f(m)≤f(1-2m),
即≤,
即m2-m+1≤(1-2m)2-(1-2m)+1,
化简得3m2-m≥0,解得m≤0或m≥,
即原不等式的解集为(-∞,0]∪[,+∞).
(2)当a∈(0,1)时,y=at为减函数.
令t=x2-x+1,则其图象的对称轴方程为x=.
要使函数f(x)在区间(2,3)上单调递增,则需满足≥3,解得a≤,所以a∈(0,].
当a∈(1,+∞)时,y=at为增函数.
要使函数f(x)在区间(2,3)上单调递增,
则需满足≤2,解得a≥,则a∈(1,+∞).
综上所述,实数a的取值范围是(0,]∪(1,+∞).
4.B 令t=ax,则原函数转化为y=t2-(3a2+1)t,其图象的对称轴为直线t=.若a>1,则x≥0时,t≥1,由于原函数在区间[0, +∞)上是增函数,则≤1,解得-≤a≤,与a>1矛盾;若05.(-2,3)
6.(1)当λ=时,f=4x-3×2x+3.
设t=2x,h(t)=t2-3t+3=(t-)2+.
又x∈[-1,2],所以t∈[,4],
则h(t)min=h()=,h(t)max=h(4)=7,
所以f(x)的值域为[,7].
(2)f(x)=4x-λ·2x+1+3=4x-2λ·2x+3,x∈[-1,2].
设t=2x,g(t)=t2-2λt+3,t∈[,4].
当λ≤时,g(t)min=g()=-λ+3=1,解得λ=,不符合题意,舍去.
当<λ<4时,g(t)min=g(λ)=-λ2+3=1,解得λ=-(舍去)或λ=.
当λ≥4时,g(t)min=g(4)=16-8λ+3=1,解得λ=,不符合题意,舍去.
综上,实数λ的值为.
7.(1)由f(x)+2g(x)=2x, ①
得f(-x)+2g(-x)=2-x.
又函数f(x),g(x)分别是定义在R上的偶函数与奇函数,所以f(x)=f(-x),g(-x)=-g(x),
所以f(x)-2g(x)=2-x. ②
由①②解得f(x)=,g(x)=.
(2)f(2x)-(m+2)g(x)+2=-(m+2)+2,
令t=2x-2-x,x∈(1,2),则t∈(,),22x+2-2x=t2+2.
因为 x∈(1,2),f(2x)-(m+2)g(x)+2≥0恒成立,所以-(m+2)+2≥0在t∈(,)上恒成立,
所以m+2≤2(t+)min,t∈(,).
因为t>0,>0,所以t+≥2=2,
当且仅当t=,即t=∈(,)时取等号,
所以m+2≤4,即m≤4-2,
所以m的最大值为4-2.
专项二 与对数函数有关的复合函数问题
1.C 由函数g(x)的图象,知g(x)≥1,函数g(x)在(-∞,1]上是减函数,在[1,+∞)上是增函数.因为对数函数y=log0.3t是减函数,所以y=log0.3g(x)≤0,且在(-∞,1]上是增函数,在[1,+∞)上是减函数.故选C.
2.ABC
3.(1)由题意,kx2-2x+6>0在x∈[2,3]上恒成立,即k>-在x∈[2,3]上恒成立.
令=u,则k>-6u2+2u在u∈[,]上恒成立.
令h(u)=-6u2+2u,u∈[,],则h(u)在[,]上单调递减,
故h(u)max=h()=0,则k>0.
故k的取值范围为(0,+∞).
(2)要使函数f(x)在区间[2,3]上为增函数,首先f(x)在区间[2,3]上恒有意义,于是由(1)可得k>0.
①当a>1时,要使函数f(x)在区间[2,3]上为增函数,则函数g(x)=kx2-2x+6在[2,3]上恒正且为增函数,故k>0且≤2,即k≥,
此时f(x)的最大值为loga(9k)=2,即k=,此时a≥,满足题意.
②当00且≥3,即0此时f(x)的最大值为loga(9k)=2,即k=(0综上,存在满足题意的实数k,k=(a≥或04.C f(x)=(lg x)2-2lg x2+3=(lg x)2-4lg x+3.令lg x=t,因为1≤x≤1 000,所以0≤t≤3.令y=t2-4t+3=(t-2)2-1,0≤t≤3,当t=2时,y取得最小值,为-1,当t=0时,y取得最大值,为3,所以f(x)的值域为[-1,3].
5.(0,)∪(8,+∞)
6.(1)令t=log4x,因为x∈[1,16],所以t∈[0,2].
令g(t)=(2t-2)(t+)=2t2-t-1=2(t-)2-,t∈[0,2],则g(t)在[0,)上单调递减,在(,2]上单调递增,
所以当t=时,g(t)取得最小值,为-,当t=2时,g(t)取得最大值,为5.
故当x∈[1,16]时,函数f(x)的值域为[-,5].
(2)不等式f(x)>2,即2t2-t-3>0,
解得t>或t<-1.
当t>时,log4x>,解得x>8;
当t<-1时,log4x<-1,解得0故不等式f(x)>2的解集为{x|08}.
(3)由于存在x∈[4,16],使得不等式f(x)所以存在t∈[1,2],使得m>2t--1成立.
因为函数y=-在[1,2]上单调递增,y=2t也在[1,2]上单调递增,
所以函数y=2t--1在[1,2]上单调递增,所以当t=1时,(2t--1)min=0,所以m>0.
故m的取值范围是(0,+∞).
专项一 与指数函数有关的复合函数问题
类型1 形如f(x)=(a>0,a≠1)的函数
1.若函数f(x)=3(2a-1)x+3在R上是减函数,则实数a的取值范围是( )
A.(-∞,) B.(,+∞)
C.(,1)∪(1,+∞) D.(,1)
2.(多选)[2022安徽蚌埠高一上期中]已知函数f(x)=(,则( )
A.f(x)的定义域为R
B.f(x)的值域为(0,2]
C.f(x)在[-2,+∞)上单调递增
D.f(x)在[-2,+∞)上单调递减
3. 已知函数f(x)=(a>0,a≠1).
(1)若a=2,解关于m的不等式f(m)-f(1-2m)≤0;
(2)若函数f(x)在区间(2,3)上单调递增,求实数a的取值范围.
类型2 形如f(x)=A(ax)2+B·ax+C(a>0,a≠1)的函数
4.若函数f(x)=ax(ax-3a2-1)(a>0,a≠1)在区间[0,+∞)上是增函数,则实数a的取值范围是( )
A.(0,] B.[,1)
C.(1,] D.[,+∞)
5.若不等式(m2-m)2x-()x<1对任意x∈(-∞,-1]恒成立,则实数m的取值范围是 .
6.[2022山东枣庄三中高一期中]已知函数f(x)=4x-λ·2x+1+3,x∈[-1,2].
(1)若λ=,求f(x)的值域;
(2)若函数f(x)的最小值为1,求实数λ的值.
类型3 形如f(x)=A(a2x+a-2x)+B(ax±a-x)+C(a>0,a≠1)的函数
7.[2022江苏南通高一上调研]已知函数f(x),g(x)分别是定义在R上的偶函数与奇函数,且f(x)+2g(x)=2x.
(1)求f(x)与g(x)的解析式;
(2)若 x∈(1,2),不等式f(2x)-(m+2)g(x)+2≥0恒成立,求实数m的最大值.
专项二 与对数函数有关的复合函数问题
类型1 形如f(x)=loga(Ax2+Bx+C)(a>0且a≠1)的函数
1.若函数g(x)=ax2+bx+c的图象如图所示,则函数y=log0.3g(x)的图象大致是( )
2.(多选)[2022重庆市第八中学校高一上期末]已知函数f(x)=log2(mx2+2x+m-1),m∈R,则下列说法正确的是( )
A.若函数f(x)的定义域为R,则实数m的取值范围是(,+∞)
B.若函数f(x)的值域为[-1,+∞),则m=2
C.若函数f(x)在[2,+∞)上为增函数,则实数m的取值范围是[0,+∞)
D.若m=0,则不等式f(x)<1的解集为(-∞,)
3.[2022黑龙江哈六中高一上期末]已知函数f(x)=loga(kx2-2x+6)(a>0且a≠1).
(1)若函数f(x)在[2,3]上恒有意义,求实数k的取值范围.
(2)是否存在实数k,使得函数f(x)在[2,3]上为增函数,且最大值为2 若存在,求出k的值;若不存在,请说明理由.
类型2 形如f(x)=A(logax)2+B·logax+C(a>0且a≠1)的函数
4.函数f(x)=(lg x)2-2lg x2+3(1≤x≤1 000)的值域为( )
A.[-1,0] B.[0,3]
C.[-1,3] D.[-1,+∞)
5.[2022重庆巴蜀中学高一上期中]设y=(log2x)2+(t-2)log2x-t+1,若t在[-2,2]上变化时,y恒取正值,则x的取值范围是 .
6.已知函数f(x)=(2log4x-2)(log4x+).
(1)当x∈[1,16]时,求该函数的值域;
(2)求不等式f(x)>2的解集;
(3)若存在x∈[4,16],使得不等式f(x)
专项一 与指数函数有关的复合函数问题
1.A 因为底数3∈(1,+∞),所以函数f(x)=3(2a-1)x+3的单调性与y=(2a-1)x+3的单调性相同.因为函数f(x)=3(2a-1)x+3在R上是减函数,所以y=(2a-1)x+3在R上是减函数,所以2a-1<0,即a<,即实数a的取值范围是(-∞,),选A.
2.ABD
3.(1)当a=2时,f(x)=.
f(m)-f(1-2m)≤0等价于f(m)≤f(1-2m),
即≤,
即m2-m+1≤(1-2m)2-(1-2m)+1,
化简得3m2-m≥0,解得m≤0或m≥,
即原不等式的解集为(-∞,0]∪[,+∞).
(2)当a∈(0,1)时,y=at为减函数.
令t=x2-x+1,则其图象的对称轴方程为x=.
要使函数f(x)在区间(2,3)上单调递增,则需满足≥3,解得a≤,所以a∈(0,].
当a∈(1,+∞)时,y=at为增函数.
要使函数f(x)在区间(2,3)上单调递增,
则需满足≤2,解得a≥,则a∈(1,+∞).
综上所述,实数a的取值范围是(0,]∪(1,+∞).
4.B 令t=ax,则原函数转化为y=t2-(3a2+1)t,其图象的对称轴为直线t=.若a>1,则x≥0时,t≥1,由于原函数在区间[0, +∞)上是增函数,则≤1,解得-≤a≤,与a>1矛盾;若0
6.(1)当λ=时,f=4x-3×2x+3.
设t=2x,h(t)=t2-3t+3=(t-)2+.
又x∈[-1,2],所以t∈[,4],
则h(t)min=h()=,h(t)max=h(4)=7,
所以f(x)的值域为[,7].
(2)f(x)=4x-λ·2x+1+3=4x-2λ·2x+3,x∈[-1,2].
设t=2x,g(t)=t2-2λt+3,t∈[,4].
当λ≤时,g(t)min=g()=-λ+3=1,解得λ=,不符合题意,舍去.
当<λ<4时,g(t)min=g(λ)=-λ2+3=1,解得λ=-(舍去)或λ=.
当λ≥4时,g(t)min=g(4)=16-8λ+3=1,解得λ=,不符合题意,舍去.
综上,实数λ的值为.
7.(1)由f(x)+2g(x)=2x, ①
得f(-x)+2g(-x)=2-x.
又函数f(x),g(x)分别是定义在R上的偶函数与奇函数,所以f(x)=f(-x),g(-x)=-g(x),
所以f(x)-2g(x)=2-x. ②
由①②解得f(x)=,g(x)=.
(2)f(2x)-(m+2)g(x)+2=-(m+2)+2,
令t=2x-2-x,x∈(1,2),则t∈(,),22x+2-2x=t2+2.
因为 x∈(1,2),f(2x)-(m+2)g(x)+2≥0恒成立,所以-(m+2)+2≥0在t∈(,)上恒成立,
所以m+2≤2(t+)min,t∈(,).
因为t>0,>0,所以t+≥2=2,
当且仅当t=,即t=∈(,)时取等号,
所以m+2≤4,即m≤4-2,
所以m的最大值为4-2.
专项二 与对数函数有关的复合函数问题
1.C 由函数g(x)的图象,知g(x)≥1,函数g(x)在(-∞,1]上是减函数,在[1,+∞)上是增函数.因为对数函数y=log0.3t是减函数,所以y=log0.3g(x)≤0,且在(-∞,1]上是增函数,在[1,+∞)上是减函数.故选C.
2.ABC
3.(1)由题意,kx2-2x+6>0在x∈[2,3]上恒成立,即k>-在x∈[2,3]上恒成立.
令=u,则k>-6u2+2u在u∈[,]上恒成立.
令h(u)=-6u2+2u,u∈[,],则h(u)在[,]上单调递减,
故h(u)max=h()=0,则k>0.
故k的取值范围为(0,+∞).
(2)要使函数f(x)在区间[2,3]上为增函数,首先f(x)在区间[2,3]上恒有意义,于是由(1)可得k>0.
①当a>1时,要使函数f(x)在区间[2,3]上为增函数,则函数g(x)=kx2-2x+6在[2,3]上恒正且为增函数,故k>0且≤2,即k≥,
此时f(x)的最大值为loga(9k)=2,即k=,此时a≥,满足题意.
②当0
5.(0,)∪(8,+∞)
6.(1)令t=log4x,因为x∈[1,16],所以t∈[0,2].
令g(t)=(2t-2)(t+)=2t2-t-1=2(t-)2-,t∈[0,2],则g(t)在[0,)上单调递减,在(,2]上单调递增,
所以当t=时,g(t)取得最小值,为-,当t=2时,g(t)取得最大值,为5.
故当x∈[1,16]时,函数f(x)的值域为[-,5].
(2)不等式f(x)>2,即2t2-t-3>0,
解得t>或t<-1.
当t>时,log4x>,解得x>8;
当t<-1时,log4x<-1,解得0
(3)由于存在x∈[4,16],使得不等式f(x)
因为函数y=-在[1,2]上单调递增,y=2t也在[1,2]上单调递增,
所以函数y=2t--1在[1,2]上单调递增,所以当t=1时,(2t--1)min=0,所以m>0.
故m的取值范围是(0,+∞).
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
