14.3.1等腰三角形(2)[上学期]
文档属性
| 名称 | 14.3.1等腰三角形(2)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 55.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-14 00:00:00 | ||
图片预览


文档简介
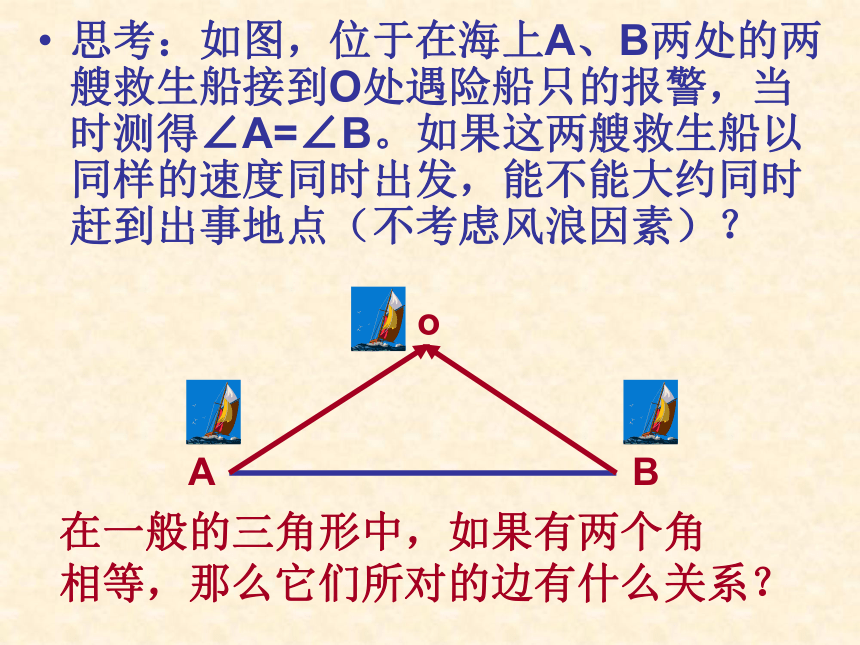
课件15张PPT。 4.13 等腰三角形14.3.1等腰三角形(2)思考:如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
在一般的三角形中,如果有两个角
相等,那么它们所对的边有什么关系?oAB判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)你能用几何证明的方法验证这个结论吗?如果:△ABC中,∠B=∠C,那么: △ABC是等腰三角形.写成几何命题试试:∴ △ABD≌△ACD( )如果一个三角形有两个角相等,
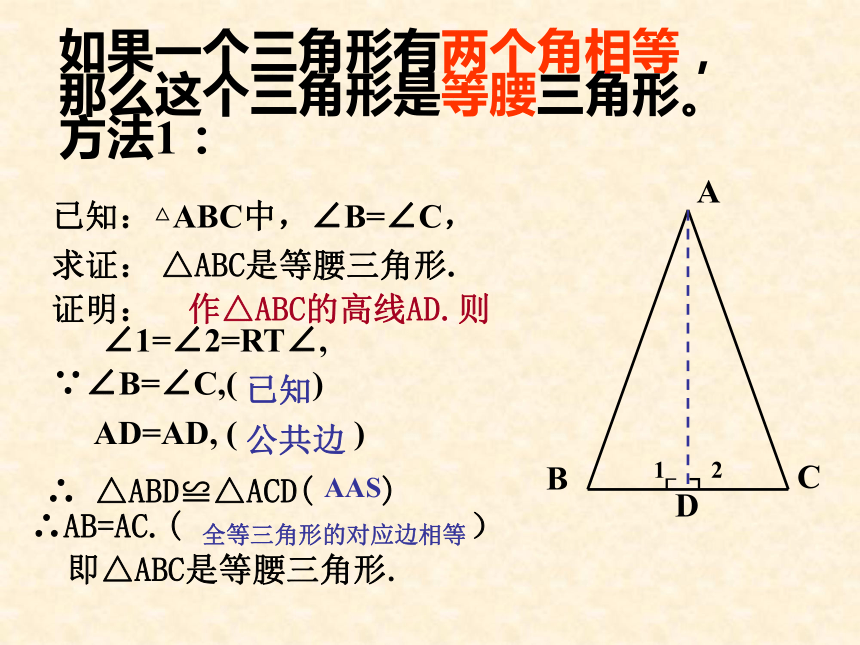
那么这个三角形是等腰三角形。
方法1:求证: △ABC是等腰三角形.已知:△ABC中,∠B=∠C,证明: 即△ABC是等腰三角形. 作△ABC的高线AD.则AAS∴AB=AC.( )全等三角形的对应边相等已知公共边∠1=∠2=RT∠,如果一个三角形有两个角相等, 那么这个三角形是等腰三角形。 方法2:已知:△ABC中,∠B=∠C.
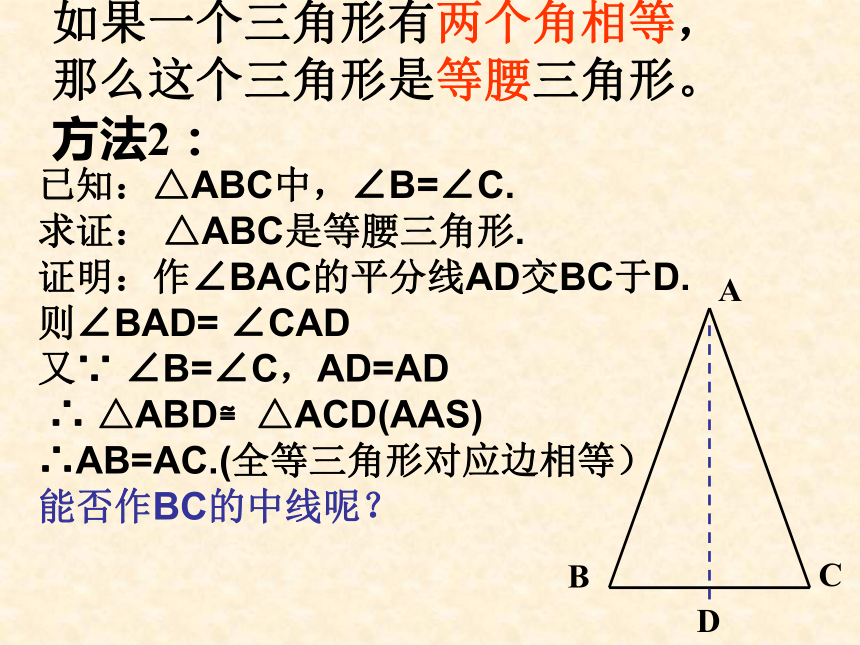
求证: △ABC是等腰三角形.
证明:作∠BAC的平分线AD交BC于D.
则∠BAD= ∠CAD
又∵ ∠B=∠C,AD=AD
∴ △ABD≌△ACD(AAS)
∴AB=AC.(全等三角形对应边相等)
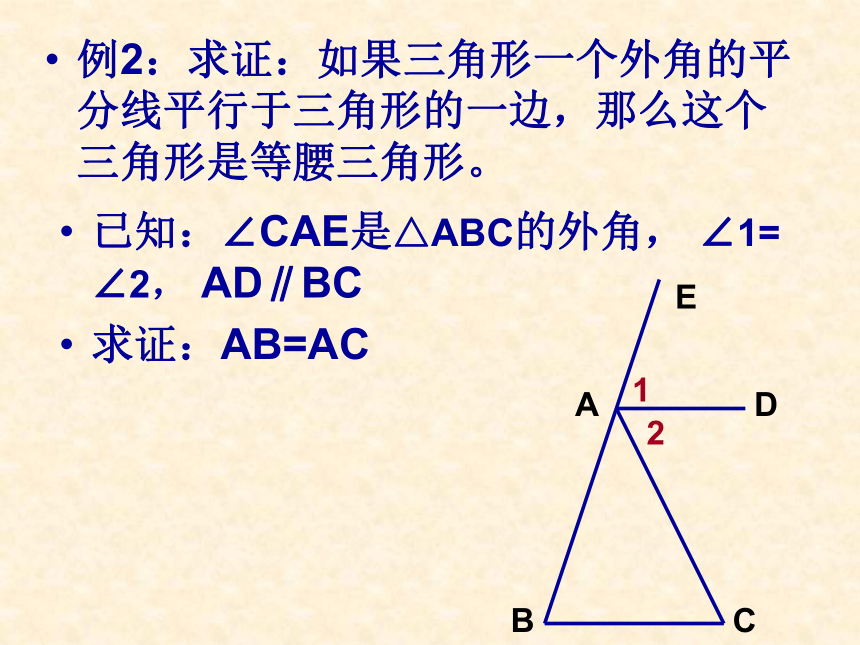
能否作BC的中线呢?例2:求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。已知:∠CAE是△ABC的外角, ∠1= ∠2, AD∥BC
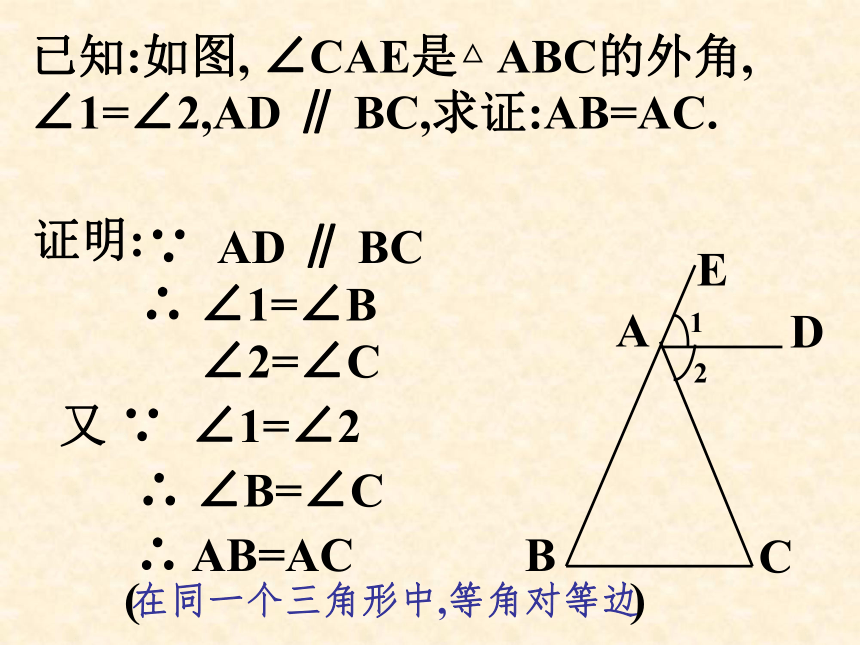
求证:AB=AC已知:如图, ∠CAE是△ ABC的外角, ∠1=∠2,AD ∥ BC,求证:AB=AC.证明:∴ ∠1=∠B ∵ AD ∥ BC ∠2=∠C ∴ ∠B=∠C又 ∵ ∠1=∠2 在同一个三角形中,等角对等边先思考,再小组合作试改变上题的条件与结论,请编出类似的问题。
已知:如图, ∠CAE是△ ABC的外角,∠1=∠2,AD ∥ BC,求证:AB=AC.(练习)已知:如图,DE ∥ BC, ∠ 1= ∠ 2.求证:BD=CE. 证明:∵ ∠ 1= ∠ 2 (已知)∴ AE=AD (在一个三角形中,等角对等边)∵ DE ∥ BC (已知)∴ ∠ 1= ∠ B,∠ 2= ∠ C (两直线平行,同位角相等) ∴ ∠ B= ∠ C,∴ AB=AC (在一个三角形中,等角对等边) ∴ AB-AD=AC-AE,即:DB=EC.(变式练习)如图∠ 1= ∠ 2 , BD=CE 。求证: DE ∥ BC。 例3:如图,标杆AB 高5m,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,绳子CD和CE要多长? 已知底边和底边上的高,你能用尺规作图方法作出这个等腰三角形吗?
如底边 是6cm,底边上的高是4cm,请作出这个等腰三角形。①定义,②判定定理 条件和结论刚好相反。在同一个三角形中小结。 作业:教材P145面内容
在一般的三角形中,如果有两个角
相等,那么它们所对的边有什么关系?oAB判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)你能用几何证明的方法验证这个结论吗?如果:△ABC中,∠B=∠C,那么: △ABC是等腰三角形.写成几何命题试试:∴ △ABD≌△ACD( )如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
方法1:求证: △ABC是等腰三角形.已知:△ABC中,∠B=∠C,证明: 即△ABC是等腰三角形. 作△ABC的高线AD.则AAS∴AB=AC.( )全等三角形的对应边相等已知公共边∠1=∠2=RT∠,如果一个三角形有两个角相等, 那么这个三角形是等腰三角形。 方法2:已知:△ABC中,∠B=∠C.
求证: △ABC是等腰三角形.
证明:作∠BAC的平分线AD交BC于D.
则∠BAD= ∠CAD
又∵ ∠B=∠C,AD=AD
∴ △ABD≌△ACD(AAS)
∴AB=AC.(全等三角形对应边相等)
能否作BC的中线呢?例2:求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。已知:∠CAE是△ABC的外角, ∠1= ∠2, AD∥BC
求证:AB=AC已知:如图, ∠CAE是△ ABC的外角, ∠1=∠2,AD ∥ BC,求证:AB=AC.证明:∴ ∠1=∠B ∵ AD ∥ BC ∠2=∠C ∴ ∠B=∠C又 ∵ ∠1=∠2 在同一个三角形中,等角对等边先思考,再小组合作试改变上题的条件与结论,请编出类似的问题。
已知:如图, ∠CAE是△ ABC的外角,∠1=∠2,AD ∥ BC,求证:AB=AC.(练习)已知:如图,DE ∥ BC, ∠ 1= ∠ 2.求证:BD=CE. 证明:∵ ∠ 1= ∠ 2 (已知)∴ AE=AD (在一个三角形中,等角对等边)∵ DE ∥ BC (已知)∴ ∠ 1= ∠ B,∠ 2= ∠ C (两直线平行,同位角相等) ∴ ∠ B= ∠ C,∴ AB=AC (在一个三角形中,等角对等边) ∴ AB-AD=AC-AE,即:DB=EC.(变式练习)如图∠ 1= ∠ 2 , BD=CE 。求证: DE ∥ BC。 例3:如图,标杆AB 高5m,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,绳子CD和CE要多长? 已知底边和底边上的高,你能用尺规作图方法作出这个等腰三角形吗?
如底边 是6cm,底边上的高是4cm,请作出这个等腰三角形。①定义,②判定定理 条件和结论刚好相反。在同一个三角形中小结。 作业:教材P145面内容
