等腰三角形复习课[上学期]
图片预览



文档简介
课件18张PPT。等腰三角形的复习 拿一张长方形的白纸,通过折叠的方法得到一个等腰三角形!
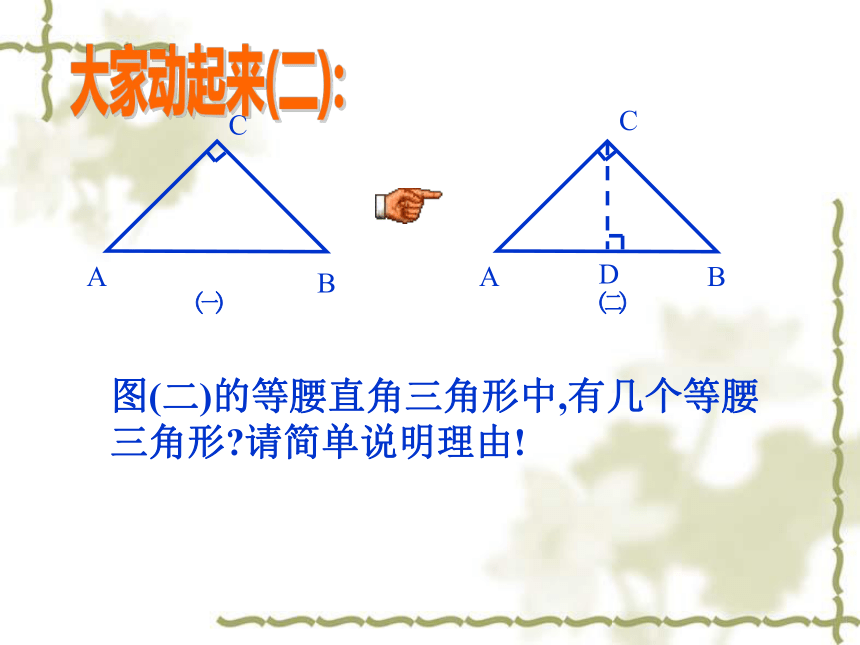
大家动起来(一):CAB图(二)的等腰直角三角形中,有几个等腰三角形?请简单说明理由!㈠大家动起来(二): 在等腰直角三角形中,折出∠CAB的平分线AE,交BC边于点E. C点在AB边上的落点为D,连结DE.
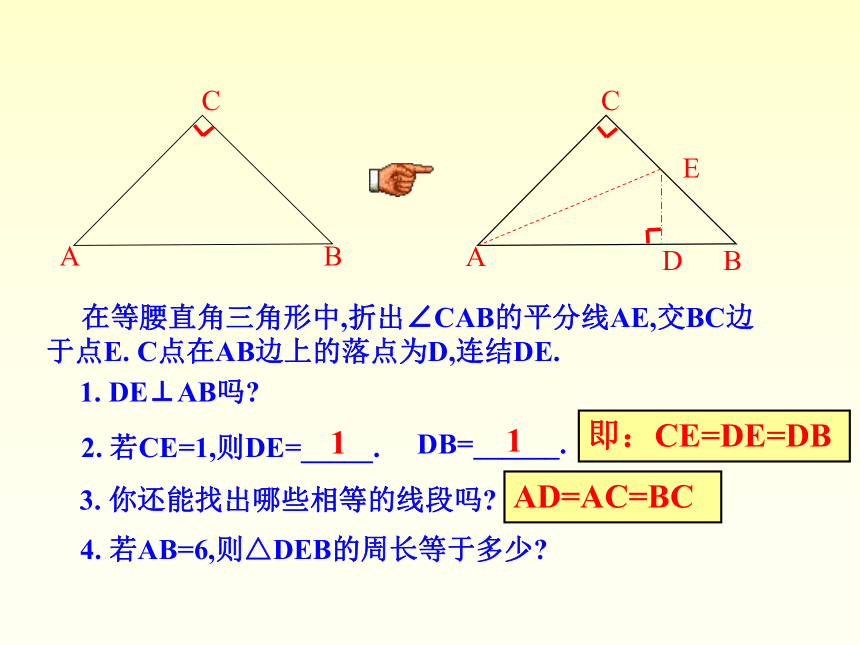
2. 若CE=1,则DE=_____.
3. 你还能找出哪些相等的线段吗? 4. 若AB=6,则△DEB的周长等于多少?
1. DE⊥AB吗?
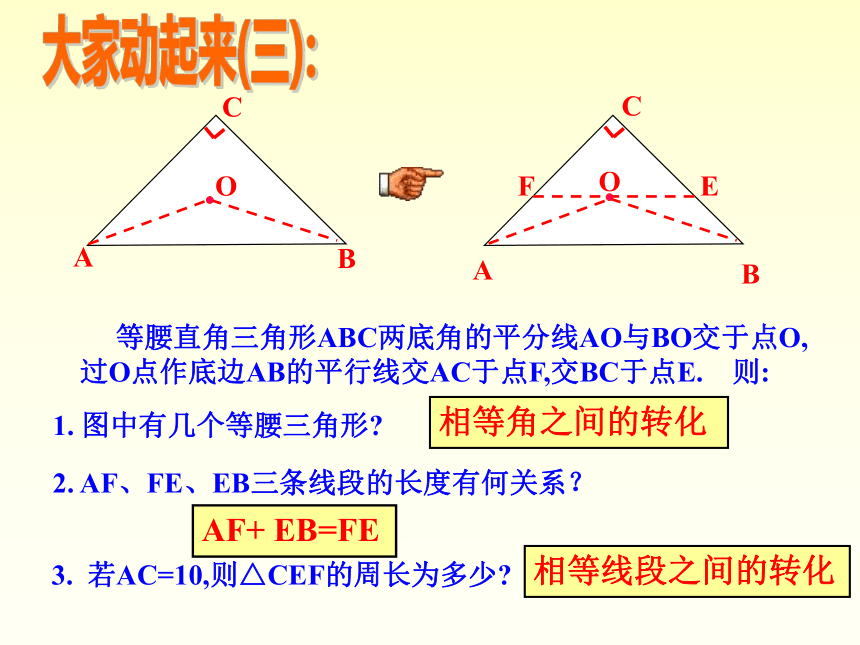
11DB=______.即:CE=DE=DBAD=AC=BCCABO 等腰直角三角形ABC两底角的平分线AO与BO交于点O, 过O点作底边AB的平行线交AC于点F,交BC于点E. 则:
3. 若AC=10,则△CEF的周长为多少?2. AF、FE、EB三条线段的长度有何关系?1. 图中有几个等腰三角形?
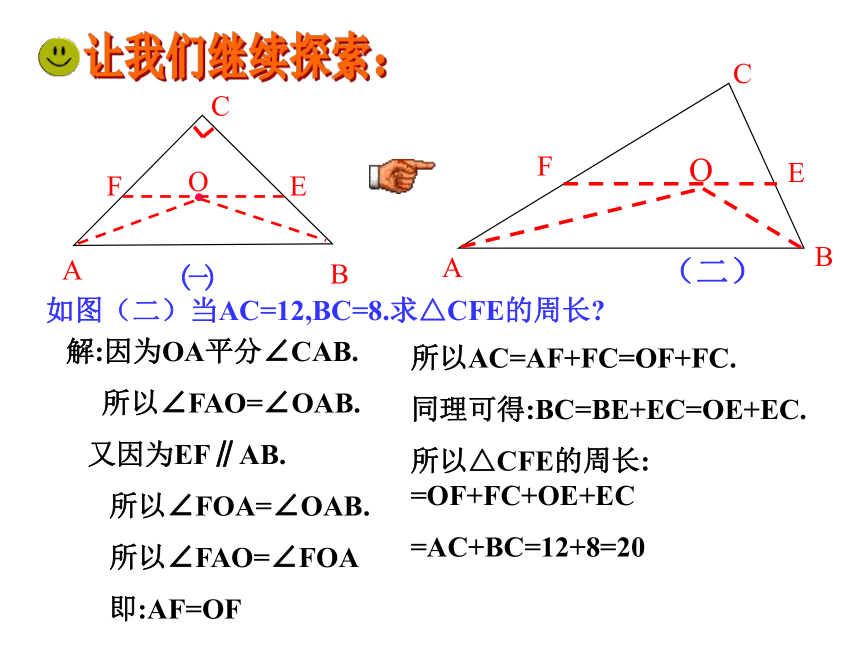
AF+ EB=FE相等角之间的转化相等线段之间的转化大家动起来(三):让我们继续探索:如图(二)当AC=12,BC=8.求△CFE的周长?
解:因为OA平分∠CAB.
所以∠FAO=∠OAB.
又因为EF∥AB.
所以∠FOA=∠OAB.
所以∠FAO=∠FOA
即:AF=OF 所以AC=AF+FC=OF+FC.
同理可得:BC=BE+EC=OE+EC.
所以△CFE的周长: =OF+FC+OE+EC
=AC+BC=12+8=20总结:(转化思想)角与角的转化: 相等角之间的代换.
边与角的转化: 等边对等角.
等角对等边.
3.边与边的转化: 相等线段之间进
行代换
(在同一个三角形)比一比!谁更快! 2. 若等腰三角形的一个内角是45°,则它的顶角为90°( ) 1.若等腰三角形两条边的长分别是5和8,则它的周长为 .21或18NO(Yes or no!)总结:在解等腰三角形的题目时,经常会运用
分类思想讨论,以防止掉入数学“陷阱”! 如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?OD150°⌒CaEFH小小探索家:总结:(分类思想)1、 角的分类2 、边的分类要注意喔!(在等腰三角形中) 数学知识: “等边对等角” 、“等角对等边”及“三线合一”
数学思想: 转化思想、分类思想!
数学策略: 构建几何模型 (基本模型与常见模型).小小演说家:通过本堂课的探索,你有何收获? 1、如果等腰三角形的一个外角为100°, 则这个等腰三角形的顶角为 。2、如图,在三角形ABC中,BC=10,AD=BD,若三角形ACD的周长为18 , 则AC长为 。课堂检测 请把这个等腰三角形纸片折成两个等腰三角形!36°⌒
ABC小小实践家(一):请把这个三角形纸片折成两个等腰三角形!小小实践家(二):小小设计家: 在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形!BAC50°110°20°小小设计家:1、对∠A进行讨论2、对∠B进行讨论3、对∠C进行讨论(分类讨论)快乐源于探索特别感谢你们的合作!祝同学们
学习进步再见
大家动起来(一):CAB图(二)的等腰直角三角形中,有几个等腰三角形?请简单说明理由!㈠大家动起来(二): 在等腰直角三角形中,折出∠CAB的平分线AE,交BC边于点E. C点在AB边上的落点为D,连结DE.
2. 若CE=1,则DE=_____.
3. 你还能找出哪些相等的线段吗? 4. 若AB=6,则△DEB的周长等于多少?
1. DE⊥AB吗?
11DB=______.即:CE=DE=DBAD=AC=BCCABO 等腰直角三角形ABC两底角的平分线AO与BO交于点O, 过O点作底边AB的平行线交AC于点F,交BC于点E. 则:
3. 若AC=10,则△CEF的周长为多少?2. AF、FE、EB三条线段的长度有何关系?1. 图中有几个等腰三角形?
AF+ EB=FE相等角之间的转化相等线段之间的转化大家动起来(三):让我们继续探索:如图(二)当AC=12,BC=8.求△CFE的周长?
解:因为OA平分∠CAB.
所以∠FAO=∠OAB.
又因为EF∥AB.
所以∠FOA=∠OAB.
所以∠FAO=∠FOA
即:AF=OF 所以AC=AF+FC=OF+FC.
同理可得:BC=BE+EC=OE+EC.
所以△CFE的周长: =OF+FC+OE+EC
=AC+BC=12+8=20总结:(转化思想)角与角的转化: 相等角之间的代换.
边与角的转化: 等边对等角.
等角对等边.
3.边与边的转化: 相等线段之间进
行代换
(在同一个三角形)比一比!谁更快! 2. 若等腰三角形的一个内角是45°,则它的顶角为90°( ) 1.若等腰三角形两条边的长分别是5和8,则它的周长为 .21或18NO(Yes or no!)总结:在解等腰三角形的题目时,经常会运用
分类思想讨论,以防止掉入数学“陷阱”! 如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?OD150°⌒CaEFH小小探索家:总结:(分类思想)1、 角的分类2 、边的分类要注意喔!(在等腰三角形中) 数学知识: “等边对等角” 、“等角对等边”及“三线合一”
数学思想: 转化思想、分类思想!
数学策略: 构建几何模型 (基本模型与常见模型).小小演说家:通过本堂课的探索,你有何收获? 1、如果等腰三角形的一个外角为100°, 则这个等腰三角形的顶角为 。2、如图,在三角形ABC中,BC=10,AD=BD,若三角形ACD的周长为18 , 则AC长为 。课堂检测 请把这个等腰三角形纸片折成两个等腰三角形!36°⌒
ABC小小实践家(一):请把这个三角形纸片折成两个等腰三角形!小小实践家(二):小小设计家: 在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形!BAC50°110°20°小小设计家:1、对∠A进行讨论2、对∠B进行讨论3、对∠C进行讨论(分类讨论)快乐源于探索特别感谢你们的合作!祝同学们
学习进步再见
