等腰三角形[上学期]
图片预览

文档简介
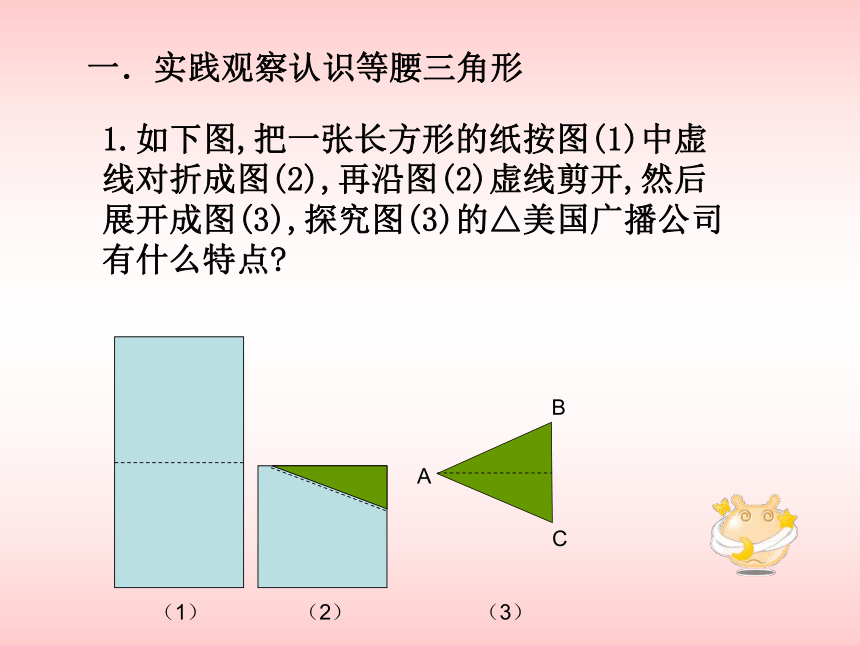
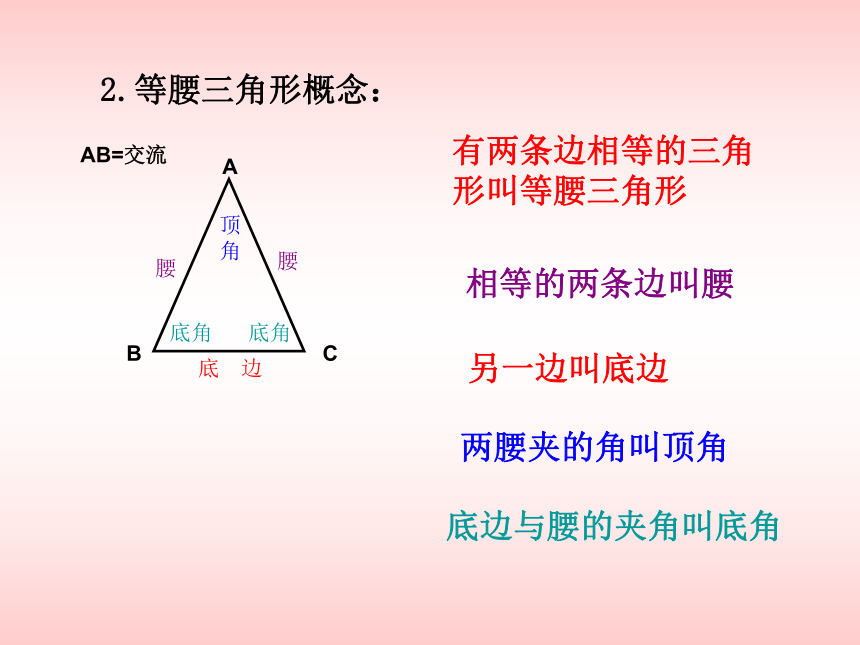
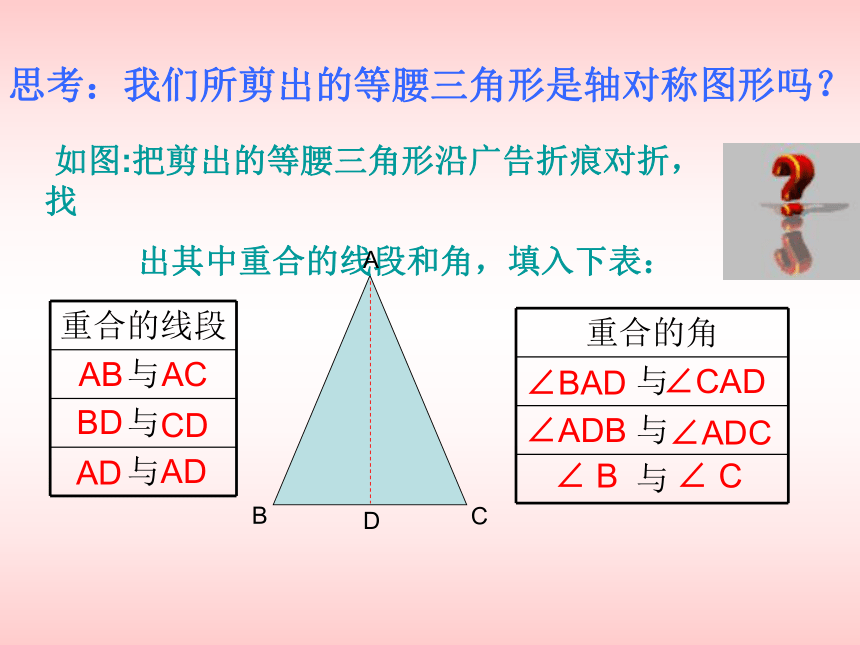
课件13张PPT。等腰三角形一.实践观察认识等腰三角形1.如下图,把一张长方形的纸按图(1)中虚线对折成图(2),再沿图(2)虚线剪开,然后展开成图(3),探究图(3)的△美国广播公司有什么特点?ABC (1) (2) (3)2.等腰三角形概念:C有两条边相等的三角形叫等腰三角形相等的两条边叫腰两腰夹的角叫顶角另一边叫底边底边与腰的夹角叫底角腰顶角底角底角AB=交流A腰B底 边思考:我们所剪出的等腰三角形是轴对称图形吗? 如图:把剪出的等腰三角形沿广告折痕对折,找
出其中重合的线段和角,填入下表:ABCD我发现了:(1)等腰三角形的两个底角相等(简写
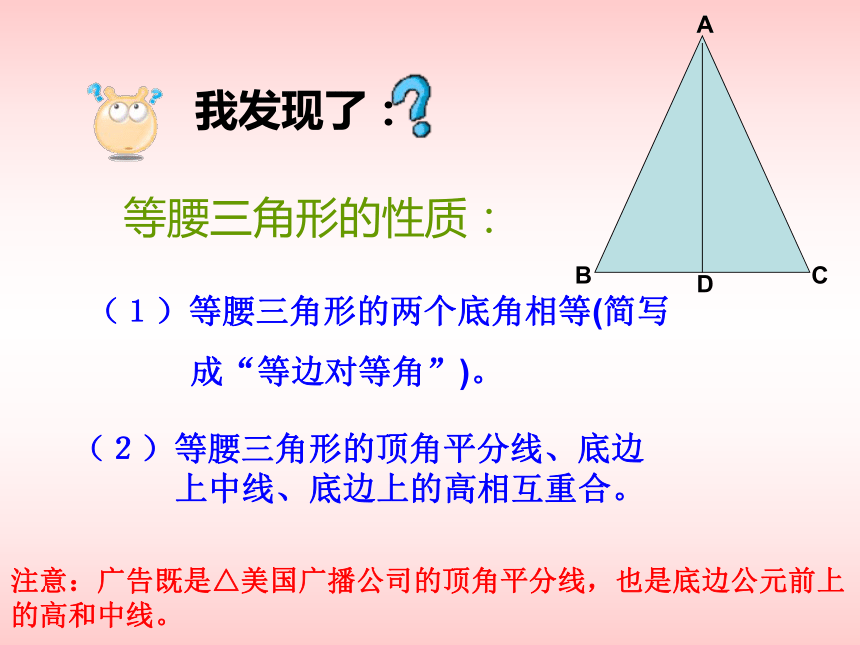
成“等边对等角”)。等腰三角形的性质:ABCD注意:广告既是△美国广播公司的顶角平分线,也是底边公元前上的高和中线。(2)等腰三角形的顶角平分线、底边
上中线、底边上的高相互重合。
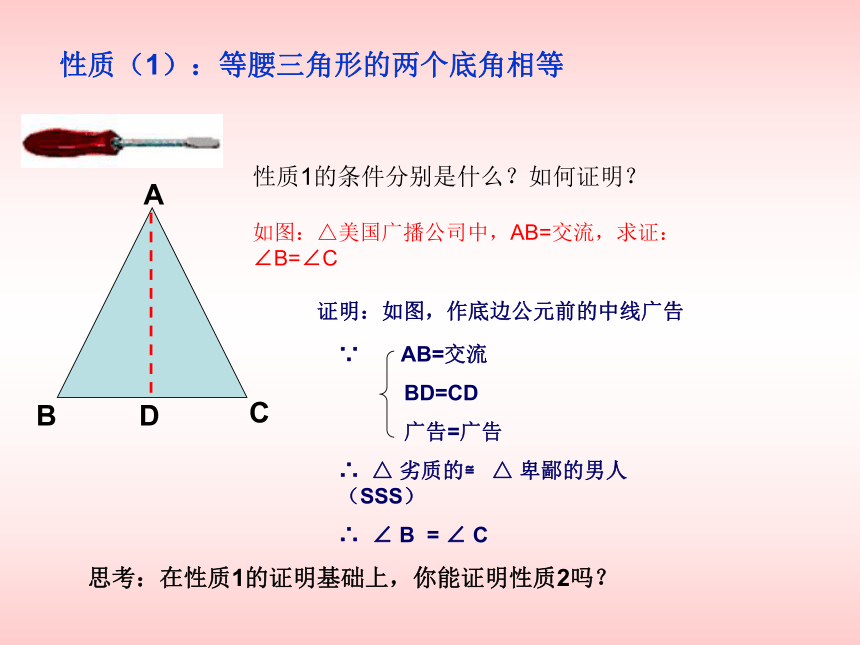
ABCD性质(1):等腰三角形的两个底角相等性质1的条件分别是什么?如何证明?如图:△美国广播公司中,AB=交流,求证:∠B=∠C证明:如图,作底边公元前的中线广告∵ AB=交流
BD=CD
广告=广告
∴ △ 劣质的≌ △ 卑鄙的男人(SSS)
∴ ∠ B = ∠ C
思考:在性质1的证明基础上,你能证明性质2吗?活动1.如图,在下列等腰三角形中,分别求出它们的底角的度数。36°120°2.如图,△美国广播公司是等腰三角形(AB=交流,∠平底渡船=90°),广告是底边公元前上的高,标出∠B、 ∠C、 ∠劣质的、 ∠DAC的度数。图中有哪些相等的线段?BCAD72°72°30°30°45°45°45°45°相等的线段有:
AB=交流,广告=BD=CD应用举例例1:如图,在△美国广播公司中,AB=交流,点D在交流上,且BD=公元前=广告,求△美国广播公司各角的度数。分折:由AB=交流,由性质1可 得_____________
DBAC设∠A=X∠美国广播公司= ∠C∠BDC= ∠C由BD=公元前,由性质1可得_____________由BD=广告,由性质1可得_____________∠A= ∠ABD应用举例例1:如图,在△美国广播公司中,AB=交流,点D在交流上,且BD=公元前=广告,求△美国广播公司各角的度数。解:∵AB=交流,BD=公元前=广告,
∴∠美国广播公司= ∠ C= ∠ BDC,
∠ A= ∠ ABD(等边对等角)
设∠ A= x ,则
∠ BDC= ∠ A+∠ ABD=2 x
从而 ∠ 美国广播公司= ∠ C= ∠ BDC=2 x
于是在△美国广播公司中,有
∠ A+ ∠ 美国广播公司+ ∠ C= x +2 x +2 x =180°
解得 x =36 °
在△ 美国广播公司中, ∠ A=36 ° , ∠ 美国广播公司= ∠ C=72 °DBAC课堂练习:ABC
(3)如图,在△美国广播公司中AB=广告=DC,∠劣质的=26 °,求∠ B和∠ C
的度数。D讨论探究:ABCDE等腰三角形底边中点到两腰的距离相等吗?F如图:△美国广播公司是等腰三角形,点D是底边公元前的中点,DE⊥AB,DF ⊥ 交流,
求证:DE=DF小结:课堂小结:这节课我们主要学习了什么内容,有哪些收获?
1、等腰三角形的有关概念
2、等腰三角形的性质:(1)等腰三角形的两个底角相等(简写成“等边
对等角”)。
(2)等腰三角形的顶角平分线、底边上中线、
底边上的高相互重合 。谢谢!再见!作业:习题14.3第4、6题
课外练习:习题14.3第3、12题
出其中重合的线段和角,填入下表:ABCD我发现了:(1)等腰三角形的两个底角相等(简写
成“等边对等角”)。等腰三角形的性质:ABCD注意:广告既是△美国广播公司的顶角平分线,也是底边公元前上的高和中线。(2)等腰三角形的顶角平分线、底边
上中线、底边上的高相互重合。
ABCD性质(1):等腰三角形的两个底角相等性质1的条件分别是什么?如何证明?如图:△美国广播公司中,AB=交流,求证:∠B=∠C证明:如图,作底边公元前的中线广告∵ AB=交流
BD=CD
广告=广告
∴ △ 劣质的≌ △ 卑鄙的男人(SSS)
∴ ∠ B = ∠ C
思考:在性质1的证明基础上,你能证明性质2吗?活动1.如图,在下列等腰三角形中,分别求出它们的底角的度数。36°120°2.如图,△美国广播公司是等腰三角形(AB=交流,∠平底渡船=90°),广告是底边公元前上的高,标出∠B、 ∠C、 ∠劣质的、 ∠DAC的度数。图中有哪些相等的线段?BCAD72°72°30°30°45°45°45°45°相等的线段有:
AB=交流,广告=BD=CD应用举例例1:如图,在△美国广播公司中,AB=交流,点D在交流上,且BD=公元前=广告,求△美国广播公司各角的度数。分折:由AB=交流,由性质1可 得_____________
DBAC设∠A=X∠美国广播公司= ∠C∠BDC= ∠C由BD=公元前,由性质1可得_____________由BD=广告,由性质1可得_____________∠A= ∠ABD应用举例例1:如图,在△美国广播公司中,AB=交流,点D在交流上,且BD=公元前=广告,求△美国广播公司各角的度数。解:∵AB=交流,BD=公元前=广告,
∴∠美国广播公司= ∠ C= ∠ BDC,
∠ A= ∠ ABD(等边对等角)
设∠ A= x ,则
∠ BDC= ∠ A+∠ ABD=2 x
从而 ∠ 美国广播公司= ∠ C= ∠ BDC=2 x
于是在△美国广播公司中,有
∠ A+ ∠ 美国广播公司+ ∠ C= x +2 x +2 x =180°
解得 x =36 °
在△ 美国广播公司中, ∠ A=36 ° , ∠ 美国广播公司= ∠ C=72 °DBAC课堂练习:ABC
(3)如图,在△美国广播公司中AB=广告=DC,∠劣质的=26 °,求∠ B和∠ C
的度数。D讨论探究:ABCDE等腰三角形底边中点到两腰的距离相等吗?F如图:△美国广播公司是等腰三角形,点D是底边公元前的中点,DE⊥AB,DF ⊥ 交流,
求证:DE=DF小结:课堂小结:这节课我们主要学习了什么内容,有哪些收获?
1、等腰三角形的有关概念
2、等腰三角形的性质:(1)等腰三角形的两个底角相等(简写成“等边
对等角”)。
(2)等腰三角形的顶角平分线、底边上中线、
底边上的高相互重合 。谢谢!再见!作业:习题14.3第4、6题
课外练习:习题14.3第3、12题
