14.3.2 十字相乘法 课件(共23张PPT)
文档属性
| 名称 | 14.3.2 十字相乘法 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-21 16:29:08 | ||
图片预览







文档简介
(共23张PPT)
14.3.2 公式法
十字相乘法
人教版八年级上册
知识回顾
因式分解的一般步骤:
(1)当多项式的各项有公因式时,应先提取公因式;当多项式的各项没有公因式时(或提取公因式后),若符合平方差公式或完全平方公式,就利用公式法分解因式;
(2)当不能直接提取公因式或用公式法分解因式时,可根据多项式的特点,把其变形为能提取公因式或能用公式法的形式,再分解因式;
(3)当乘积中的每一个因式都不能再分解时,因式分解就结束了.
教学目标
1.了解掌握并熟练运用x2+(p+q)x+pq型式子进行因式分解的方法.
2.能熟练运用适当方法对ax2+bx+c进行分解因式,及相关计算.
新知导入
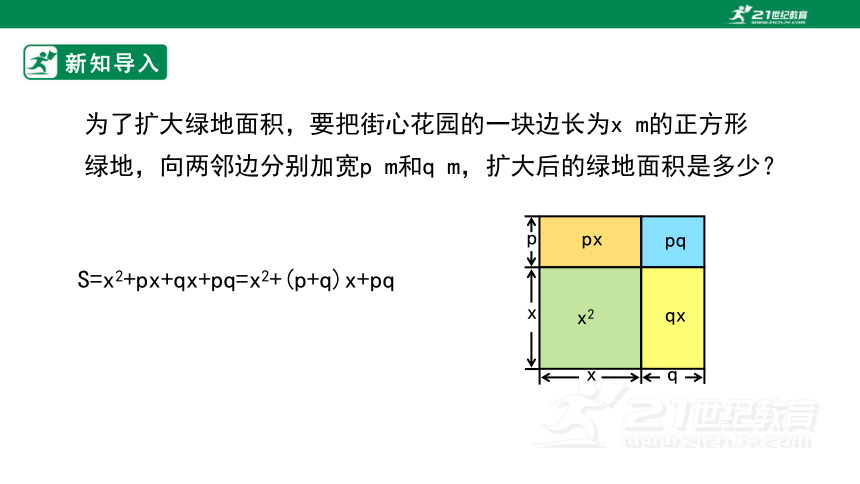
为了扩大绿地面积,要把街心花园的一块边长为x m的正方形绿地,向两邻边分别加宽p m和q m,扩大后的绿地面积是多少?
S=x2+px+qx+pq=x2+(p+q)x+pq
x
x
p
q
x2
px
pq
qx
新知探究
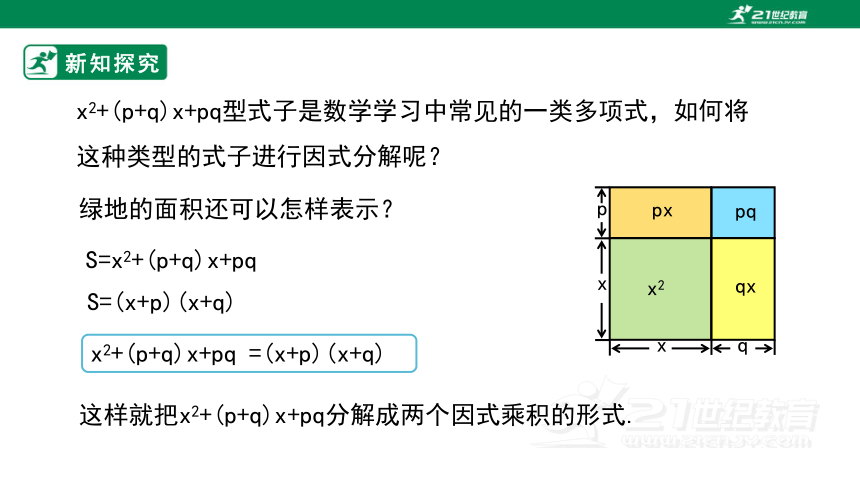
x2+(p+q)x+pq型式子是数学学习中常见的一类多项式,如何将这种类型的式子进行因式分解呢?
绿地的面积还可以怎样表示?
x
x
p
q
x2
px
pq
qx
S=x2+(p+q)x+pq
S=(x+p)(x+q)
x2+(p+q)x+pq =(x+p)(x+q)
这样就把x2+(p+q)x+pq分解成两个因式乘积的形式.
新知探究
因式分解与整式乘法是方向相反的变形,利用这种关系可以得出:
x2+(p+q)x+pq=(x+p)(x+q)
x2+(p+q)x+pq型式子的因式分解
利用上式,可以将某些二次三项式进行因式分解.
新知探究
x2+(p+q)x+pq=(x+p)(x+q)
十字相乘法分解因式的步骤:
(1)分解二次项,将二次项x2写成两个数的乘积形式(x2=x×x),分别写在十字交叉线的左上角和左下角;
x
p
x
q
(2)分解常数项(pq=p×q),分别写在十字交叉线的右上角和右下角;
(3)交叉相乘,求代数和,检验结果是否等于一次项,px+qx=(p+q)x.
(4)将十字交叉线上端两数相加、下端两数也相加,分别作为因式分解结果的一个因式相乘,得到分解因式的结果。
(x+p)
(x+q)
新知典例
例1 分解因式:
(1) x2-3x+2;
分析:(1)①
x
-1
x
-2
②检验:x×(-2)+x×(-1)=-3x
解:(1) x2-3x+2= ;
③得出因式
(x-1)
(x-2)
(x-1)(x-2)
当常数项是正数时,可以分解成两个同号的数的积,符号与一次项的符号相同;
新知典例
(2) x2+3x-10.
分析:(2)①
x
5
x
-2
②检验:x×(-2)+x×5=3x
解:(2) x2+3x-10= ;
③得出因式
(x+5)
(x-2)
(x+5)(x-2)
当常数项是负数时,可以分解成两个异号的数的积,绝对值大的因数的符号与一次项的符号相同;
新知练习
1.(1)x2﹣2x﹣15
(1)原式=(x﹣5)(x+3)
x
-5
x
3
分析:
(2)x2﹣6x+8
(2)原式=(x﹣2)(x﹣4)
x
-2
x
-4
分析:
新知探究
对于形如关于x的二次三项式ax2+bx+c,如何使用十字相乘法进行分解因式呢?
(1)二次项系数a分解成a1与a2的积,分别写在十字交叉线的左上角和左下角;
(2)常数项c分解成c1与c2的积,分别写在十字交叉线的右上角和右下角
(3)把a1,a2,c1,c2按如图所示方式排列,当且仅当a1c2x+a2c1x=bx(一次项系数)时,ax2+bx+c可分解因式.
即ax2+bx+c=(a1x+c1)(a2x+c2).
a1x
c1
a2x
c2
(a1x+c1)
(a2x+c2)
新知典例
例2. 分解因式
(1)2x2﹣x﹣6
分析:(1)①
2x
3
x
-2
②检验:2x×(-2)+x×3=-x
解:(1) 2x2﹣x﹣6= ;
(2x+3)
(x-2)
(2x+3)(x﹣2)
③得出因式
新知典例
(2)10x2+x﹣21
分析:(1)①
2x
3
5x
-7
解:(1) 10x2+x﹣21= ;
(2x+3)
(5x-7)
(2x+3)(5x﹣7)
新知练习
2.分解因式
(1)3x2﹣19x﹣14; (2)6a2﹣13ab+6b2
(1)原式=(3x+2)(x﹣7)
3x
2
x
-7
分析:
(2)原式=(2a﹣3b)(3a﹣2b)
2a
-3b
3a
-2b
分析:
新知探究
能不能用十字相乘法分解多项式a2+2ab+b2 ?
a
b
a
b
①
②检验:a×b+a×b=2ab
(a+b)
(a+b)
③得出因式
经过3个步骤我们可以得出a2+2ab+b2分解的结果为(a+b)(a+b)=(a+b)2,所以可以看出完全平方公式也是一种十字相乘法的运用,平方差公式是不是也是用的十字相乘法呢?
新知探究
例3 十字相乘分解因式a2-b2
分析:中间项为0,a2可以分解为a×a,b2可以分解为-b×b
a
-b
a
b
①
②检验:a×b-a×b=0
(a-b)
(a+b)
③得出因式
∴a2-b2=(a+b)(a-b)
∴平方差公式也是可以使用十字相乘法进行分解因式的。
由此可以看出“十字相乘法”是一种非常强大的分解因式方法。
课堂总结
十字相乘法因式分解
x2+(p+q)x+pq型式子的因式分解
十字相乘法
x
p
x
q
qx+px=(q+p)x
ax2+bx+c型式子的因式分解
十字相乘法
a1c2x+a2c1x=bx
a1x
c1
a2x
c2
反思:其实完全平方公式也是十字相乘法
课堂练习
1.分解因式:
(2)(x﹣y)2+(x﹣y)﹣6
(2)原式=(x﹣y+3)(x﹣y﹣2)
(1)x2﹣3x+2
(1)原式=(x﹣1)(x﹣2)
课堂练习
2.(2019·淄博)分解因式:x3+5x2+6x=___________.
x(x+2)(x+3)
1
2
1
3
1×3+1×2=5
分析:x3+5x2+6x
=x(x2+5x+6)
=x(x+2)(x+3).
课堂练习
3.(2019·威海)分解因式:2x2-6x+4=__________.
2(x-1)(x-2)
1
-2
1
-1
1×(-1)+1×(-2)=5
分析:2x2-6x+4
=2(x2-3x+2)
=2(x-1)(x-2).
课堂练习
(1)﹣4a3b3+6a2b﹣2ab
4.因式分解:
(2)a3﹣5a2﹣6a
解:(1)原式=﹣2ab(2a2b2﹣3ab+1)
=﹣2ab(2ab﹣1)(ab﹣1)
(2)原式=a(a2﹣5a﹣6)
=a(a﹣6)(a+1)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
14.3.2 公式法
十字相乘法
人教版八年级上册
知识回顾
因式分解的一般步骤:
(1)当多项式的各项有公因式时,应先提取公因式;当多项式的各项没有公因式时(或提取公因式后),若符合平方差公式或完全平方公式,就利用公式法分解因式;
(2)当不能直接提取公因式或用公式法分解因式时,可根据多项式的特点,把其变形为能提取公因式或能用公式法的形式,再分解因式;
(3)当乘积中的每一个因式都不能再分解时,因式分解就结束了.
教学目标
1.了解掌握并熟练运用x2+(p+q)x+pq型式子进行因式分解的方法.
2.能熟练运用适当方法对ax2+bx+c进行分解因式,及相关计算.
新知导入
为了扩大绿地面积,要把街心花园的一块边长为x m的正方形绿地,向两邻边分别加宽p m和q m,扩大后的绿地面积是多少?
S=x2+px+qx+pq=x2+(p+q)x+pq
x
x
p
q
x2
px
pq
qx
新知探究
x2+(p+q)x+pq型式子是数学学习中常见的一类多项式,如何将这种类型的式子进行因式分解呢?
绿地的面积还可以怎样表示?
x
x
p
q
x2
px
pq
qx
S=x2+(p+q)x+pq
S=(x+p)(x+q)
x2+(p+q)x+pq =(x+p)(x+q)
这样就把x2+(p+q)x+pq分解成两个因式乘积的形式.
新知探究
因式分解与整式乘法是方向相反的变形,利用这种关系可以得出:
x2+(p+q)x+pq=(x+p)(x+q)
x2+(p+q)x+pq型式子的因式分解
利用上式,可以将某些二次三项式进行因式分解.
新知探究
x2+(p+q)x+pq=(x+p)(x+q)
十字相乘法分解因式的步骤:
(1)分解二次项,将二次项x2写成两个数的乘积形式(x2=x×x),分别写在十字交叉线的左上角和左下角;
x
p
x
q
(2)分解常数项(pq=p×q),分别写在十字交叉线的右上角和右下角;
(3)交叉相乘,求代数和,检验结果是否等于一次项,px+qx=(p+q)x.
(4)将十字交叉线上端两数相加、下端两数也相加,分别作为因式分解结果的一个因式相乘,得到分解因式的结果。
(x+p)
(x+q)
新知典例
例1 分解因式:
(1) x2-3x+2;
分析:(1)①
x
-1
x
-2
②检验:x×(-2)+x×(-1)=-3x
解:(1) x2-3x+2= ;
③得出因式
(x-1)
(x-2)
(x-1)(x-2)
当常数项是正数时,可以分解成两个同号的数的积,符号与一次项的符号相同;
新知典例
(2) x2+3x-10.
分析:(2)①
x
5
x
-2
②检验:x×(-2)+x×5=3x
解:(2) x2+3x-10= ;
③得出因式
(x+5)
(x-2)
(x+5)(x-2)
当常数项是负数时,可以分解成两个异号的数的积,绝对值大的因数的符号与一次项的符号相同;
新知练习
1.(1)x2﹣2x﹣15
(1)原式=(x﹣5)(x+3)
x
-5
x
3
分析:
(2)x2﹣6x+8
(2)原式=(x﹣2)(x﹣4)
x
-2
x
-4
分析:
新知探究
对于形如关于x的二次三项式ax2+bx+c,如何使用十字相乘法进行分解因式呢?
(1)二次项系数a分解成a1与a2的积,分别写在十字交叉线的左上角和左下角;
(2)常数项c分解成c1与c2的积,分别写在十字交叉线的右上角和右下角
(3)把a1,a2,c1,c2按如图所示方式排列,当且仅当a1c2x+a2c1x=bx(一次项系数)时,ax2+bx+c可分解因式.
即ax2+bx+c=(a1x+c1)(a2x+c2).
a1x
c1
a2x
c2
(a1x+c1)
(a2x+c2)
新知典例
例2. 分解因式
(1)2x2﹣x﹣6
分析:(1)①
2x
3
x
-2
②检验:2x×(-2)+x×3=-x
解:(1) 2x2﹣x﹣6= ;
(2x+3)
(x-2)
(2x+3)(x﹣2)
③得出因式
新知典例
(2)10x2+x﹣21
分析:(1)①
2x
3
5x
-7
解:(1) 10x2+x﹣21= ;
(2x+3)
(5x-7)
(2x+3)(5x﹣7)
新知练习
2.分解因式
(1)3x2﹣19x﹣14; (2)6a2﹣13ab+6b2
(1)原式=(3x+2)(x﹣7)
3x
2
x
-7
分析:
(2)原式=(2a﹣3b)(3a﹣2b)
2a
-3b
3a
-2b
分析:
新知探究
能不能用十字相乘法分解多项式a2+2ab+b2 ?
a
b
a
b
①
②检验:a×b+a×b=2ab
(a+b)
(a+b)
③得出因式
经过3个步骤我们可以得出a2+2ab+b2分解的结果为(a+b)(a+b)=(a+b)2,所以可以看出完全平方公式也是一种十字相乘法的运用,平方差公式是不是也是用的十字相乘法呢?
新知探究
例3 十字相乘分解因式a2-b2
分析:中间项为0,a2可以分解为a×a,b2可以分解为-b×b
a
-b
a
b
①
②检验:a×b-a×b=0
(a-b)
(a+b)
③得出因式
∴a2-b2=(a+b)(a-b)
∴平方差公式也是可以使用十字相乘法进行分解因式的。
由此可以看出“十字相乘法”是一种非常强大的分解因式方法。
课堂总结
十字相乘法因式分解
x2+(p+q)x+pq型式子的因式分解
十字相乘法
x
p
x
q
qx+px=(q+p)x
ax2+bx+c型式子的因式分解
十字相乘法
a1c2x+a2c1x=bx
a1x
c1
a2x
c2
反思:其实完全平方公式也是十字相乘法
课堂练习
1.分解因式:
(2)(x﹣y)2+(x﹣y)﹣6
(2)原式=(x﹣y+3)(x﹣y﹣2)
(1)x2﹣3x+2
(1)原式=(x﹣1)(x﹣2)
课堂练习
2.(2019·淄博)分解因式:x3+5x2+6x=___________.
x(x+2)(x+3)
1
2
1
3
1×3+1×2=5
分析:x3+5x2+6x
=x(x2+5x+6)
=x(x+2)(x+3).
课堂练习
3.(2019·威海)分解因式:2x2-6x+4=__________.
2(x-1)(x-2)
1
-2
1
-1
1×(-1)+1×(-2)=5
分析:2x2-6x+4
=2(x2-3x+2)
=2(x-1)(x-2).
课堂练习
(1)﹣4a3b3+6a2b﹣2ab
4.因式分解:
(2)a3﹣5a2﹣6a
解:(1)原式=﹣2ab(2a2b2﹣3ab+1)
=﹣2ab(2ab﹣1)(ab﹣1)
(2)原式=a(a2﹣5a﹣6)
=a(a﹣6)(a+1)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
