物理人教版(2019)必修第二册8.1功和功率(共65张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册8.1功和功率(共65张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-10-20 00:00:00 | ||
图片预览








文档简介
(共65张PPT)
第一节 功与功率
必修二 第八章 机械能守恒定律
力学中功的定义
一个力作用在物体上,物体在这个力的方向上移动了一段距离,力学里就说这个力做了功。
一、知识回顾
接下来请同学们来分析A、B、C、D四组做功的实例,并请同学们分析是否做功,如果不做功,为什么?
从实例中体会一下“做功的必要因素”;
F
F
S
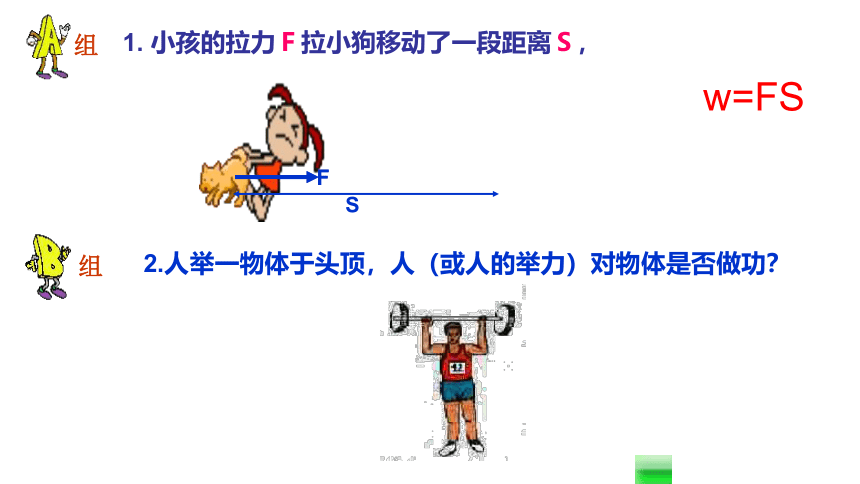
1. 小孩的拉力F拉小狗移动了一段距离S,
组
w=FS
2.人举一物体于头顶,人(或人的举力)对物体是否做功?
组
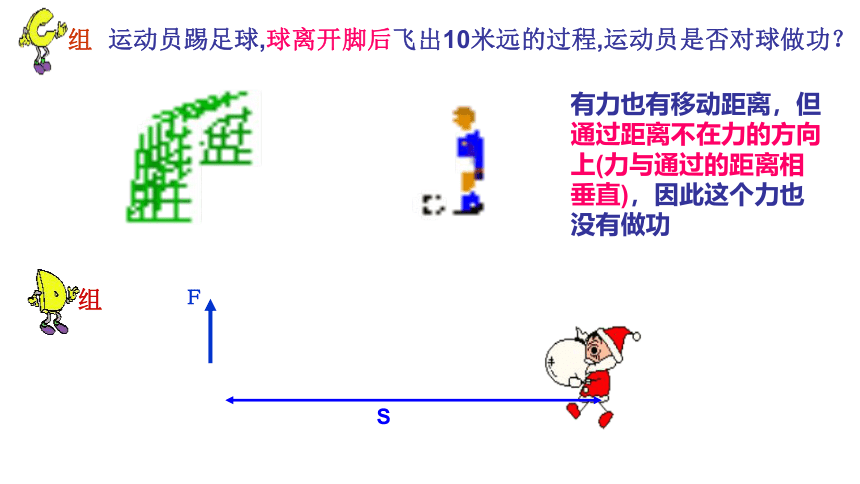
运动员踢足球,球离开脚后飞出10米远的过程,运动员是否对球做功?
组
F
组
S
有力也有移动距离,但通过距离不在力的方向上(力与通过的距离相垂直),因此这个力也没有做功
做功的两个必要因素是
1.有力作用在物体上 F
2.物体在这个力的方向上移动了一段距离 s
必要因素
必须需要,同时满足,缺一不可
1.怎样才算做功?
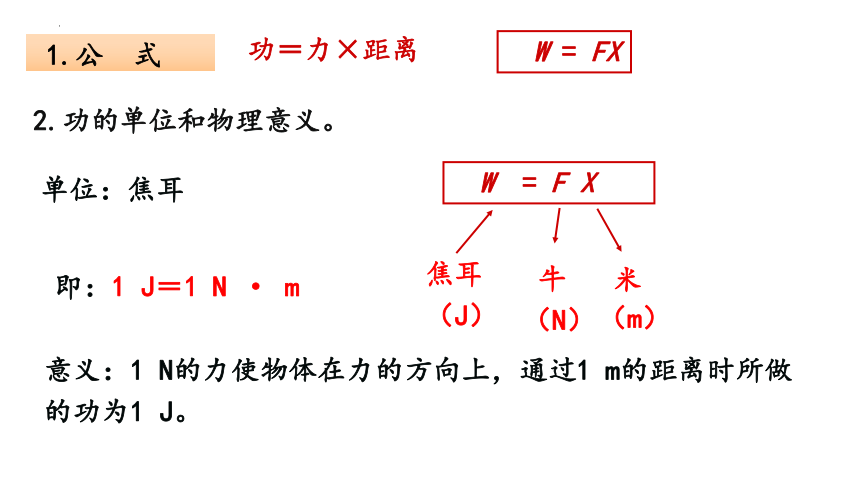
功=力×距离
W = FX
1.公 式
2.功的单位和物理意义。
牛(N)
米 (m)
焦耳(J)
即:1 J=1 N · m
W = F X
意义:1 N的力使物体在力的方向上,通过1 m的距离时所做的功为1 J。
单位:焦耳
功如何计算?
初中关于“功”的知识
当力F的方向与物体运动方向一致时:
功的公式:W=Fx
问:当力F的方向与物体运动方向不一致时功如何计算?
x
F
F
α
x
F
α
x
F
=Fcosα
F1
F2
α
x
F
x2
x1=xcosα
求该过程中F做的功?
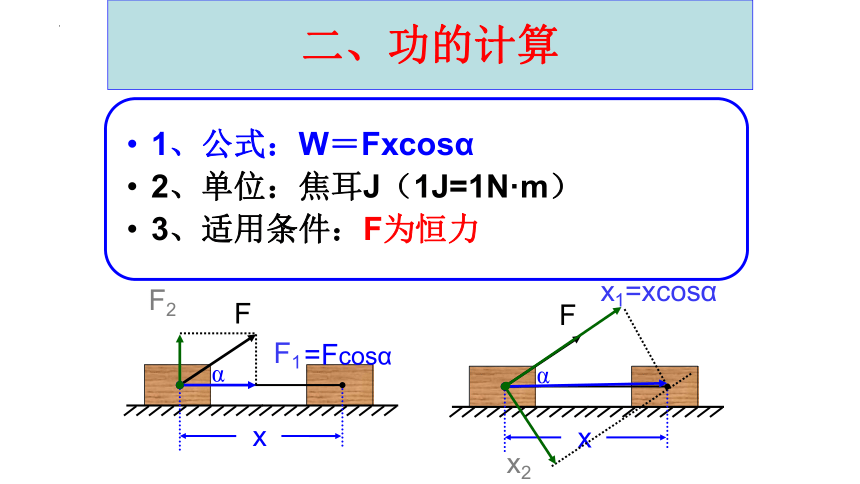
二、功的计算
1、公式:W=Fxcosα
2、单位:焦耳J(1J=1N·m)
3、适用条件:F为恒力
α
x
F
=Fcosα
F1
F2
α
x
F
x2
x1=xcosα
F
m
[例题1]:如图所示,绳的一端固定在天花板上,通过一动滑轮将质量m=10kg的物体由静止开始以2m/s2的加速度提升3s。求绳的另一端拉力F在这3s内所做的功。(g=10m/s2,滑轮和绳的质量及摩擦均不计)
m
F
[结论1]:⑴公式 中的l意义是:力的作用点的位移,不是物体的位移,但一般相等(动滑轮除外);
⑵动滑轮:省力不省功,滑轮左边绳子拉力不做功,可以说“等效”
⒊意义与性质:
⑴物理意义:描述力在空间上的积累效果;
⑵功是过程量,必须与一个过程、一段位移相对应
三、功的正负分析
当0≤α<900时,cosα>0,W>0
力对物体做正功
表明这个力是动力
对物体的运动起促进作用
α
x
F
功的正负分析
当α=900时,cosα=0,W=0
力对物体不做功
α
x
F
当900<α≤1800时, cosα<0,W<0
力对物体做负功
表明这个力是阻力
对物体的运动起阻碍作用
α
x
F
注意:当一个力做了负功也可以说成物体克服这个力做了多少正功。
功的正负分析
三、功的正负
1、功是标量但有±
功是能量转化的量度;
能量是标量,所以功也是标量
2、功的正负的含义
力对物体做正功,表明这个力对物体运动有促进作用,是动力.
力对物体做负功,表明这个力对物体运动有促进作用,是阻力.
3、正负的判定方法
公式法判定
做功效果判定
注
当一个力做了负功也可以说成物体克服这个力做了多少正功。
某一个力做了正功,物体不一定加速;某一个力做了负功,物体不一定减速;但合力做正功,物体一定加速。
判断下列四图力做功的正负:
表示力F的有向线段的箭尾与表示速度的有向线段
的箭尾重合后,看两有向线段的夹角。
丙图30度
甲图30度
丁图0度
乙图150度
如图所示,物体质量为m=10kg,受到与水平方向成370角的力F=50N作用,从静止开始运动了5m,已知物体与地面间的动摩擦因数μ=0.4,g=10m/s2,sin370=0.6,cos370=0.8
则力F对物体做的功WF= ,
重力对物体做的功WG= ,
支持力对物体做的功WN= ,
摩擦力对物体做的功Wf= ,
合力对物体做的功W= 。
实例分析
37°
F
四、总功的计算
功是标量,运算法则是:代数运算
方法1:
总功等于各个力对物体做功的代数和
W合=W1+W2+W3+…
方法2:
总功等于合外力对物体做的功
W合= F合·Xcosα(合力恒定)
[例题1]如图所示,一个质量为m=1kg的木块,放在倾角为α=370的斜面体上,当斜面与木块保持相对静止沿水平方向向右匀速移动距离s=10m的过程中,作用在木块上的各个力分别做功多少?合力的功是多少?(重力加速度为g)
重力做功为0,
支持力做功为 ,
摩擦力做功为 ,
合力做功为0.
[例题2]:如图所示,一质量为m=1kg的物体静止在光滑水平地面上。F1和F2是作用在物体上的两个水平恒力,大小分别为F1=3N,F2=4N,且方向相互垂直。在这两个力共同作用下,使物体沿水平面运动t=2s的过程中,则:
⑴该物体的加速度和位移分别是多少?
⑵F1、F2对物体各做多少功?它们对物体做功的代数和是多少?
⑶合力做功是多少?
F1
F2
A
B
(乙)
F
xB
A
B
A
B
xA
L
(甲)
F
[例题3]:如图甲所示,长为L=1m的木板B放在水平地面上,质量为m=1kg物块A(可看作质点)放在B的右端,用力F作用在物体B上使B向右运动xB=3m时,A恰好到达B的左端,A、B两物体之间的动摩擦因数为μ=0.5,g=10m/s2。试求:⑴A、B之间的滑动摩擦力为多大?⑵A对B的滑动摩擦力对B做了多少功?⑶B对A的滑动摩擦力对A做了多少功?⑷两滑动摩擦力做功的代数和是多少?⑸若将物块A用细线固定在左边墙壁上,如图乙所示,则当将B从A底下抽出时B对A的滑动摩擦力对A做多少功? A对B的滑动摩擦力对B做了多少功?
(甲)
A
B
A
B
x
F
A
B
(乙)
F
[例题4]:如图甲所示,长木板B放在光滑水平地面上,物块A(可看作质点)放在B的右端,A、B质量均为m=1kg用力F=4N作用在物体B上,使A、B保持相对静止一起向右匀加速运动,时间t=2s。⑴A、B之间的静摩擦力为多大?位移多大?⑵A、B之间的静摩擦力对A、B分别做了多少功?做功代数和是多少?⑶若将物块A用细线固定在左边墙壁上,如图乙所示,当用力F=4N作用在物体B上时,A、B均未被拉动,则t=2s内A、B之间的静摩擦力对A、B分别做了多少功?
[结论㈠]:
⑴滑动摩擦力可能做正功、负功,还可能不做功
⑵相互作用的一对滑动摩擦力,做功大小可能不相等,做功的代数和为负值
(3)静摩擦力可能做正功、负功,还可能不做功
(4)相互作用的一对静摩擦力,做功大小相等,做功的代数和为零
C
B
h2
h1
A
[例题5]:如图所示,三个斜面A、B、C,其中斜面A、B的竖直高度均为h1=3m,但倾角不同。斜面C的竖直高度为h2=4m。质量为m=1kg的物体分别从三个斜面的顶端滑到斜面底端,g=10m/s2。试求:
⑴三种情况下重力做的功分别是多少?
⑵若物体从斜面A的底端上升到顶端,重力做功为多少?
①重力做功的表达式:
②上升→负功,下降→正功;
③重力做功只与竖直高度有关,与斜面倾角无关;
h
如图所示,质量为m=1kg的物体从一高为h=3m的曲面的顶端滑到底端,g=10m/s2。试求:重力做的功是多少?
①微元法:将轨迹分割成许多小段,每一小段可看作一个斜面;
②重力做功只与竖直高度有关;
h
h
如图所示,质量为m=1kg的小球从左边斜面下滑,初始高度为h=3m,然后小球滑上右边斜面,上升的高度相同,g=10m/s2。试求:整个过程重力做的功是多少?
[结论(二)]:⑴公式:
⑵正负:上升→负功,下降→正功;
⑶特点:重力做功与路径无关,只与始末位置(高度差)有关
[注]:⑴摩擦力的恒定性具有阶段性;
⑵①保守力:力所作的功与路径无关,仅由质点的始末位置决定, 沿闭和路径所做的功为零(如重力、弹力);
②非保守力:力所做的功不仅决定于受力质点的始末位置,而且和质点经过的路径有关,即力沿闭和路径所做的功不等于零(如摩擦力);
③保守力不一定是变力;
图像法
平均法
变力做功:方向不变,大小均匀变化
[例题5]如图所示,一根劲度系数为k=100N/m的轻质弹簧放置在光滑水平地面上,其左端固定在竖直墙壁上,若用一水平力将弹簧右端向右缓慢拉动距离为x=0.5m,则:
⑴试在图中作出弹簧弹力随伸长量之间的函数图象;
⑵试求弹簧弹力做功的大小是多少?
x/m
F/N
O
0.2
0.4
20
40
Fˊ
x
变力做功:方向变化
[例题6]如图所示,一个质量为m=1kg的物体放在粗糙的圆盘上随盘一起转动一周,物体距圆盘中心轴的距离为R=1m,且始终与盘保持相对静止。试求:
⑴若圆盘匀速转动,物体所受静摩擦所做的功是多少?
⑵若使大小不变的力F=10N作用于物体上,F的方向任何时刻都沿圆弧切线与速度方向一致,则力F做功大小是多少?
ω
m
微元法
1、如图所示,一个质量为m=2.0 kg的物体放在倾角为α=37°的固定斜面上,现用F=30 N、平行于斜面的力拉物体使其由静止开始沿斜面向上运动。已知物体与斜面之间的动摩擦因数μ=0.50,斜面足够长,g取10 m/s2,sin 37°=0.60,cos 37°=0.80。物体运动2 s后,关于各力做功情况,下列说法中正确的是( )
A.重力做功为-120 J
B.摩擦力做功为-80 J
C.拉力做功为100 J
D.物体所受的合力做功为100 J
ABD
2、如图所示,水平弹簧劲度系数k=500N/m,现用一外力推物块,使弹簧压缩10cm而静止。突然撤去外力F,物块被弹开的过程,弹簧对物块做了多少功?(弹簧与物体未连接)
F
⑴公式法:
⑵面积法:如图所示;
O
x/m
F/N
0.1
50
A
O
B
3、如图所示,摆球质量为m=1kg,悬线的长为L=1m,把悬线拉到水平位置后放手,设在摆球运动过程中空气阻力f=1N大小不变,求摆球从A运动到竖直位置B时,绳的拉力T、重力mg、空气阻力f各做了多少功?
;
定义:功与完成这些功所用时间的比值,叫作功率。
1 W=1 J/s
①物理意义:描述力对物体做功的快慢。
②单位:瓦特(国际单位制),简称瓦,符号是 W
③功率是标量,且无负值。
一、功率
1kW=1000W
一个物体在水平恒力 F 的作用下,以速度 v 匀速直线运动了一段时间t,在这段时间t 内恒力F 做功的功率多大
一个沿着物体位移方向的力对物体做功的功率, 等于这个力与物体速度的乘积。
思考:当力F 和位移l之间有一夹角α时,如何表示功率?
v
F
α
v1
v2
F
α
v
F2
F1
P=vFcosα
P=Fvcosα
P=Fvcosα
二、平均功率与瞬时功率
(1)平均功率反映一段时间、一个过程内做功的整体快慢程度;
(2)瞬时功率反映一个时刻、一个位置时做功的瞬间快慢程度;
P=Fvcosa
若v表示平均速度,则P表示平均功率
若v表示瞬时速度,则P表示瞬时功率
(1)功率的定义式,适用于任何情况下的功率计算,一般用来求平均功率
(2)功率大小不由W或者t决定,反映做功的快慢程度
存在制约关系:
①当P一定时,F与v成反比
②当v一定时,P与F成正比
③当F一定时,P与v成正比
[例题1]:重100N的物体做自由落体运动,在第1s内,重力的平均功率是多少?在1s末的瞬时功率呢?(g=10m/s2)
G=100N
所以:
同理:
v瞬=gt=10m/s
⒈额定功率:机器长时间正常工作的最大功率,也就是发动机铭牌上的标称值,是反映机器性能的一项重要指标;
⒉实际功率:实际工作时的功率,可以小于或等于额定功率,不能大于额定功率,否则会损坏机器;
三、额定功率与实际功率
1、如图所示,质量m=2kg的木块在倾角为θ=370的斜面上由静止开始下滑,木块与斜面间的动摩擦因数μ=0.5,已知sin370=0.6,cos370=0.8,取g=10m/s2,斜面足够长。求:
⑴前2s内重力的功率;
⑵第1s内、第2s内重力的功率分别是多少;
⑶2s末重力的功率;
[例题2]:一辆电动自行车的铭牌上给出了如下的技术参数:①规格:车型26"电动自行车,整车质量m1=30kg,最大载量120kg;②后轮驱动直流永磁体电机:额定输出功率120w,额定电压40V,额定电流3.5A(即输入电动机的功率为40×3.5W=140W)。质量为m2=70kg的人骑此自行车沿平直公路上行驶,所受阻力恒为车和人的总重的k=0.02倍,g=10m/s2。求:
⑴此车的电机在额定功率下正常工作时的效率η;
⑵仅让电动机在额定功率提供动力的情况下,人骑自行车匀速行驶时的速度;
⑶仅让电机在额定功率提供动力的情况下,当车速为v1=1.0m/s时,人骑车的加速度大小。
汽车的功率:汽车在行驶的过程中,发动机的最大功率等于额定功率。
P = F v
汽车功率(油门)
汽车的牵引力
汽车的瞬时速度
汽车加速运动的情况有两种:
1、以额定功率P启动;
2、在恒定的牵引力F作用下匀加速启动。
机车启动问题
汽车的功率中的几个物理量:
P额:额定功率 P:实际功率 F:牵引力
v:瞬时速度 F阻:阻力
G
F
FN
F阻
机车启动问题
类型1:机车以恒定功率 P 启动
思考:汽车在行驶时受到哪些力?
(P不变,F阻不变)
思考:随着汽车启动汽车速度如何变化?
汽车所受牵引力又是如何变化?如何判断?
汽车速度V逐渐增大
P = F v
v增大
P不变
F 减小
思考:汽车启动过程中加速度如何变化?如何判断?
由牛顿第二定律
F- F阻= ma
F 减小
F阻不变
a减小
思考:汽车启动过程中做什么运动?
加速度减小的加速直线运动
机车启动问题
类型1:机车以恒定功率 P 启动
思考:汽车加速度减到0之后做什么运动?
匀速直线运动
思考:汽车匀速时速度如何求解?
汽车匀速
a=0
F=F阻
P = F vm=F阻vm
G
F
FN
F阻
P
F阻
vm=
当F=F阻时,
a=0 ,v达到最大
保持
vm
匀速
v
F=
v
P
a=
m
F-F阻
↑
→
↓
↑
→
→
↓
↓
vm=
F阻
P
加速度逐渐减小的加速直线运动
匀速直线运动
类型1:机车以恒定功率 P 启动
机车启动问题
v- t 图像
机车启动问题
类型1:机车以恒定功率 P 启动
P- t 图像
F- t 图像
vm
v- t 图像
v
t
0
机车启动问题
类型1:机车以恒定功率 P 启动
P- t 图像
P
t
0
P
vm=
F阻
F
t
0
F- t 图像
F阻
[例1]汽车发动机的额定功率为60KW,汽车的质量为5t,汽车在水平路面上行驶时,阻力是车重的0.1倍,g=10m/s2。汽车保持额定功率不变从静止启动后:
①汽车所能达到的最大速度是多大?
②当汽车的速度为5m/s时加速度多大?
③当汽车的加速度为2m/s2时速度多大?
12m/s
4m/s
1.4m/s2
例题分析
[练习]一辆重5 t的汽车,发动机的额定功率为80 kW.汽车从静止开始以额定功率启动,车受的阻力为车重的0.06倍.(g取10 m/s2)求
(1) 汽车以额定功率做匀速运动的最终速度多大?
(2) 汽车速度为20 m/s时,加速度多大?
答案: (1)26.7 m/s (2)0.2 m/s2
机车启动问题
类型2:机车以恒定加速度 a 启动
(a不变,F阻不变)
G
F
FN
F阻
由牛顿第二定律
F- F阻= ma
F 不变
F阻不变
a不变
又:P = F v
F不变
V增大
P增大
思考:汽车输出功率P能否无限制增加?
不能,输出功率最大等于额定功率
当:P =P额
当汽车达到额定功率后功率P不变,回到类型1,以恒定功率运动。
机车启动问题
类型2:机车以恒定加速度 a 启动
当:P =P额=F v
v增大
P不变
F 减小
F- F阻= ma
F 减小
F阻不变
a减小
汽车匀速
a=0
F=F阻
P额 = F vm=F阻vm
P额
vm=
F阻
当F= F阻时,
a=0 ,v达到最大
保持
vm
匀速
F=
v
P额
a=
m
F-F阻
↑
→
↓
v
↑
↓
→
→
↓
vm=
F阻
P额
加速度逐渐减小的加速直线运动
匀速直线运动
a=
m
F-F阻
→
→
→
→
F
→
v
↑
P=F v
↑
↑
→
当P= P额时,保持P额继续加速
匀加速直线运动
类型2:机车以恒定加速度 a 启动
一、机车启动问题
v- t 图像
机车启动问题
P- t 图像
F- t 图像
类型2:机车以恒定加速度 a 启动
v
t
0
vm=
F阻
P额
vm
机车启动问题
类型2:机车以恒定加速度 a 启动
v- t 图像
P- t 图像
F- t 图像
P
t
0
P额
t1
t2
v1
t1
F
t
0
F=F阻+ma
t1
t2
F阻
P = F v=Fat
v
t
0
vm=
F阻
P额
vm
机车启动问题
类型2:机车以恒定加速度 a 启动
P
t
0
P额
t1
t2
v1
t1
F
t
0
F=F阻+ma
t1
t2
F阻
P = F v=Fat
思考:如何求解v1 、t1?
由牛顿第二定律
F- F阻= ma
F=F阻+ma
v1 :P=P额=FV1
v1=
F阻+ma
P额
t1=
a
V1
由V=V0+at
=
(F阻+ma)a
P额
1.没有达到最大速度时,有瞬时加速度。
2.达到最大速度时,a=0 F牵=f
注意:发动机的功率是指牵引力的功率而不是指合外力或阻力的功率。
汽车的两种运动状态
机车启动问题
[例2]汽车在水平路面以a=2m/s2,从静止启动做匀加速直线运动,汽车额定功率为80KW,汽车能达到的最大速度为20m/s,质量为2t,汽车在水平路面上行驶时,所受阻力不变,g=10m/s2。
①汽车所受阻力为多大?
②汽车匀加速运动的时间是多少?
③汽车3s末的速度多大?
④汽车速度为16m/s时末的加速度多大?
F阻=4000N
v=6m/s
t=5s
例题分析
a1=0.5m/s2
[练习2]水平面上静止放置一质量为m=0.2 kg 的物块,固定在同一水平面上的小型电动机通过水平细线牵引物块,使物块由静止开始做匀加速直线运动,2 s末达到额定功率,其v -t图线如图所示,物块与水平面间的动摩擦因数为μ=0.1,取g=10 m/s2,电动机与物块间的距离足够长.求:
(1)物块做匀加速直线运动时受到的牵引力大小;
(2)电动机的额定功率;
(3)物块在电动机牵引下,最终能达到的最大速度.
答案: (1)0.28 N
(2)0.224 W
(3)1.12 m/s
从P = Fv可以看出,汽车、火车等交通工具和各种起重机械,当发动机的输出功率P一定时,牵引力F与速度v成反比。你认为应该怎样增大它们的牵引力呢?
从P=Fv可以看出,汽车当发动机的功率P一定时,牵引力F与速度成反比,要增大牵引力,就要减小速度。
汽车的输出功率
汽车的牵引力
汽车的瞬时速度
(油门)
发动机输出的功率不能无限制地增大,所以汽车上坡时,司机要用“换挡”的办法减小速度,来得到较大的牵引力。
不过,在发动机功率一定时,通过减小速度提高牵引力或通过减小牵引力而提高速度,效果都是有限的。所以,要提高速度和增大牵引力,必须提高发动机的额定功率,这就是高速火车、汽车和大型舰船需要大功率发动机的原因。
第一节 功与功率
必修二 第八章 机械能守恒定律
力学中功的定义
一个力作用在物体上,物体在这个力的方向上移动了一段距离,力学里就说这个力做了功。
一、知识回顾
接下来请同学们来分析A、B、C、D四组做功的实例,并请同学们分析是否做功,如果不做功,为什么?
从实例中体会一下“做功的必要因素”;
F
F
S
1. 小孩的拉力F拉小狗移动了一段距离S,
组
w=FS
2.人举一物体于头顶,人(或人的举力)对物体是否做功?
组
运动员踢足球,球离开脚后飞出10米远的过程,运动员是否对球做功?
组
F
组
S
有力也有移动距离,但通过距离不在力的方向上(力与通过的距离相垂直),因此这个力也没有做功
做功的两个必要因素是
1.有力作用在物体上 F
2.物体在这个力的方向上移动了一段距离 s
必要因素
必须需要,同时满足,缺一不可
1.怎样才算做功?
功=力×距离
W = FX
1.公 式
2.功的单位和物理意义。
牛(N)
米 (m)
焦耳(J)
即:1 J=1 N · m
W = F X
意义:1 N的力使物体在力的方向上,通过1 m的距离时所做的功为1 J。
单位:焦耳
功如何计算?
初中关于“功”的知识
当力F的方向与物体运动方向一致时:
功的公式:W=Fx
问:当力F的方向与物体运动方向不一致时功如何计算?
x
F
F
α
x
F
α
x
F
=Fcosα
F1
F2
α
x
F
x2
x1=xcosα
求该过程中F做的功?
二、功的计算
1、公式:W=Fxcosα
2、单位:焦耳J(1J=1N·m)
3、适用条件:F为恒力
α
x
F
=Fcosα
F1
F2
α
x
F
x2
x1=xcosα
F
m
[例题1]:如图所示,绳的一端固定在天花板上,通过一动滑轮将质量m=10kg的物体由静止开始以2m/s2的加速度提升3s。求绳的另一端拉力F在这3s内所做的功。(g=10m/s2,滑轮和绳的质量及摩擦均不计)
m
F
[结论1]:⑴公式 中的l意义是:力的作用点的位移,不是物体的位移,但一般相等(动滑轮除外);
⑵动滑轮:省力不省功,滑轮左边绳子拉力不做功,可以说“等效”
⒊意义与性质:
⑴物理意义:描述力在空间上的积累效果;
⑵功是过程量,必须与一个过程、一段位移相对应
三、功的正负分析
当0≤α<900时,cosα>0,W>0
力对物体做正功
表明这个力是动力
对物体的运动起促进作用
α
x
F
功的正负分析
当α=900时,cosα=0,W=0
力对物体不做功
α
x
F
当900<α≤1800时, cosα<0,W<0
力对物体做负功
表明这个力是阻力
对物体的运动起阻碍作用
α
x
F
注意:当一个力做了负功也可以说成物体克服这个力做了多少正功。
功的正负分析
三、功的正负
1、功是标量但有±
功是能量转化的量度;
能量是标量,所以功也是标量
2、功的正负的含义
力对物体做正功,表明这个力对物体运动有促进作用,是动力.
力对物体做负功,表明这个力对物体运动有促进作用,是阻力.
3、正负的判定方法
公式法判定
做功效果判定
注
当一个力做了负功也可以说成物体克服这个力做了多少正功。
某一个力做了正功,物体不一定加速;某一个力做了负功,物体不一定减速;但合力做正功,物体一定加速。
判断下列四图力做功的正负:
表示力F的有向线段的箭尾与表示速度的有向线段
的箭尾重合后,看两有向线段的夹角。
丙图30度
甲图30度
丁图0度
乙图150度
如图所示,物体质量为m=10kg,受到与水平方向成370角的力F=50N作用,从静止开始运动了5m,已知物体与地面间的动摩擦因数μ=0.4,g=10m/s2,sin370=0.6,cos370=0.8
则力F对物体做的功WF= ,
重力对物体做的功WG= ,
支持力对物体做的功WN= ,
摩擦力对物体做的功Wf= ,
合力对物体做的功W= 。
实例分析
37°
F
四、总功的计算
功是标量,运算法则是:代数运算
方法1:
总功等于各个力对物体做功的代数和
W合=W1+W2+W3+…
方法2:
总功等于合外力对物体做的功
W合= F合·Xcosα(合力恒定)
[例题1]如图所示,一个质量为m=1kg的木块,放在倾角为α=370的斜面体上,当斜面与木块保持相对静止沿水平方向向右匀速移动距离s=10m的过程中,作用在木块上的各个力分别做功多少?合力的功是多少?(重力加速度为g)
重力做功为0,
支持力做功为 ,
摩擦力做功为 ,
合力做功为0.
[例题2]:如图所示,一质量为m=1kg的物体静止在光滑水平地面上。F1和F2是作用在物体上的两个水平恒力,大小分别为F1=3N,F2=4N,且方向相互垂直。在这两个力共同作用下,使物体沿水平面运动t=2s的过程中,则:
⑴该物体的加速度和位移分别是多少?
⑵F1、F2对物体各做多少功?它们对物体做功的代数和是多少?
⑶合力做功是多少?
F1
F2
A
B
(乙)
F
xB
A
B
A
B
xA
L
(甲)
F
[例题3]:如图甲所示,长为L=1m的木板B放在水平地面上,质量为m=1kg物块A(可看作质点)放在B的右端,用力F作用在物体B上使B向右运动xB=3m时,A恰好到达B的左端,A、B两物体之间的动摩擦因数为μ=0.5,g=10m/s2。试求:⑴A、B之间的滑动摩擦力为多大?⑵A对B的滑动摩擦力对B做了多少功?⑶B对A的滑动摩擦力对A做了多少功?⑷两滑动摩擦力做功的代数和是多少?⑸若将物块A用细线固定在左边墙壁上,如图乙所示,则当将B从A底下抽出时B对A的滑动摩擦力对A做多少功? A对B的滑动摩擦力对B做了多少功?
(甲)
A
B
A
B
x
F
A
B
(乙)
F
[例题4]:如图甲所示,长木板B放在光滑水平地面上,物块A(可看作质点)放在B的右端,A、B质量均为m=1kg用力F=4N作用在物体B上,使A、B保持相对静止一起向右匀加速运动,时间t=2s。⑴A、B之间的静摩擦力为多大?位移多大?⑵A、B之间的静摩擦力对A、B分别做了多少功?做功代数和是多少?⑶若将物块A用细线固定在左边墙壁上,如图乙所示,当用力F=4N作用在物体B上时,A、B均未被拉动,则t=2s内A、B之间的静摩擦力对A、B分别做了多少功?
[结论㈠]:
⑴滑动摩擦力可能做正功、负功,还可能不做功
⑵相互作用的一对滑动摩擦力,做功大小可能不相等,做功的代数和为负值
(3)静摩擦力可能做正功、负功,还可能不做功
(4)相互作用的一对静摩擦力,做功大小相等,做功的代数和为零
C
B
h2
h1
A
[例题5]:如图所示,三个斜面A、B、C,其中斜面A、B的竖直高度均为h1=3m,但倾角不同。斜面C的竖直高度为h2=4m。质量为m=1kg的物体分别从三个斜面的顶端滑到斜面底端,g=10m/s2。试求:
⑴三种情况下重力做的功分别是多少?
⑵若物体从斜面A的底端上升到顶端,重力做功为多少?
①重力做功的表达式:
②上升→负功,下降→正功;
③重力做功只与竖直高度有关,与斜面倾角无关;
h
如图所示,质量为m=1kg的物体从一高为h=3m的曲面的顶端滑到底端,g=10m/s2。试求:重力做的功是多少?
①微元法:将轨迹分割成许多小段,每一小段可看作一个斜面;
②重力做功只与竖直高度有关;
h
h
如图所示,质量为m=1kg的小球从左边斜面下滑,初始高度为h=3m,然后小球滑上右边斜面,上升的高度相同,g=10m/s2。试求:整个过程重力做的功是多少?
[结论(二)]:⑴公式:
⑵正负:上升→负功,下降→正功;
⑶特点:重力做功与路径无关,只与始末位置(高度差)有关
[注]:⑴摩擦力的恒定性具有阶段性;
⑵①保守力:力所作的功与路径无关,仅由质点的始末位置决定, 沿闭和路径所做的功为零(如重力、弹力);
②非保守力:力所做的功不仅决定于受力质点的始末位置,而且和质点经过的路径有关,即力沿闭和路径所做的功不等于零(如摩擦力);
③保守力不一定是变力;
图像法
平均法
变力做功:方向不变,大小均匀变化
[例题5]如图所示,一根劲度系数为k=100N/m的轻质弹簧放置在光滑水平地面上,其左端固定在竖直墙壁上,若用一水平力将弹簧右端向右缓慢拉动距离为x=0.5m,则:
⑴试在图中作出弹簧弹力随伸长量之间的函数图象;
⑵试求弹簧弹力做功的大小是多少?
x/m
F/N
O
0.2
0.4
20
40
Fˊ
x
变力做功:方向变化
[例题6]如图所示,一个质量为m=1kg的物体放在粗糙的圆盘上随盘一起转动一周,物体距圆盘中心轴的距离为R=1m,且始终与盘保持相对静止。试求:
⑴若圆盘匀速转动,物体所受静摩擦所做的功是多少?
⑵若使大小不变的力F=10N作用于物体上,F的方向任何时刻都沿圆弧切线与速度方向一致,则力F做功大小是多少?
ω
m
微元法
1、如图所示,一个质量为m=2.0 kg的物体放在倾角为α=37°的固定斜面上,现用F=30 N、平行于斜面的力拉物体使其由静止开始沿斜面向上运动。已知物体与斜面之间的动摩擦因数μ=0.50,斜面足够长,g取10 m/s2,sin 37°=0.60,cos 37°=0.80。物体运动2 s后,关于各力做功情况,下列说法中正确的是( )
A.重力做功为-120 J
B.摩擦力做功为-80 J
C.拉力做功为100 J
D.物体所受的合力做功为100 J
ABD
2、如图所示,水平弹簧劲度系数k=500N/m,现用一外力推物块,使弹簧压缩10cm而静止。突然撤去外力F,物块被弹开的过程,弹簧对物块做了多少功?(弹簧与物体未连接)
F
⑴公式法:
⑵面积法:如图所示;
O
x/m
F/N
0.1
50
A
O
B
3、如图所示,摆球质量为m=1kg,悬线的长为L=1m,把悬线拉到水平位置后放手,设在摆球运动过程中空气阻力f=1N大小不变,求摆球从A运动到竖直位置B时,绳的拉力T、重力mg、空气阻力f各做了多少功?
;
定义:功与完成这些功所用时间的比值,叫作功率。
1 W=1 J/s
①物理意义:描述力对物体做功的快慢。
②单位:瓦特(国际单位制),简称瓦,符号是 W
③功率是标量,且无负值。
一、功率
1kW=1000W
一个物体在水平恒力 F 的作用下,以速度 v 匀速直线运动了一段时间t,在这段时间t 内恒力F 做功的功率多大
一个沿着物体位移方向的力对物体做功的功率, 等于这个力与物体速度的乘积。
思考:当力F 和位移l之间有一夹角α时,如何表示功率?
v
F
α
v1
v2
F
α
v
F2
F1
P=vFcosα
P=Fvcosα
P=Fvcosα
二、平均功率与瞬时功率
(1)平均功率反映一段时间、一个过程内做功的整体快慢程度;
(2)瞬时功率反映一个时刻、一个位置时做功的瞬间快慢程度;
P=Fvcosa
若v表示平均速度,则P表示平均功率
若v表示瞬时速度,则P表示瞬时功率
(1)功率的定义式,适用于任何情况下的功率计算,一般用来求平均功率
(2)功率大小不由W或者t决定,反映做功的快慢程度
存在制约关系:
①当P一定时,F与v成反比
②当v一定时,P与F成正比
③当F一定时,P与v成正比
[例题1]:重100N的物体做自由落体运动,在第1s内,重力的平均功率是多少?在1s末的瞬时功率呢?(g=10m/s2)
G=100N
所以:
同理:
v瞬=gt=10m/s
⒈额定功率:机器长时间正常工作的最大功率,也就是发动机铭牌上的标称值,是反映机器性能的一项重要指标;
⒉实际功率:实际工作时的功率,可以小于或等于额定功率,不能大于额定功率,否则会损坏机器;
三、额定功率与实际功率
1、如图所示,质量m=2kg的木块在倾角为θ=370的斜面上由静止开始下滑,木块与斜面间的动摩擦因数μ=0.5,已知sin370=0.6,cos370=0.8,取g=10m/s2,斜面足够长。求:
⑴前2s内重力的功率;
⑵第1s内、第2s内重力的功率分别是多少;
⑶2s末重力的功率;
[例题2]:一辆电动自行车的铭牌上给出了如下的技术参数:①规格:车型26"电动自行车,整车质量m1=30kg,最大载量120kg;②后轮驱动直流永磁体电机:额定输出功率120w,额定电压40V,额定电流3.5A(即输入电动机的功率为40×3.5W=140W)。质量为m2=70kg的人骑此自行车沿平直公路上行驶,所受阻力恒为车和人的总重的k=0.02倍,g=10m/s2。求:
⑴此车的电机在额定功率下正常工作时的效率η;
⑵仅让电动机在额定功率提供动力的情况下,人骑自行车匀速行驶时的速度;
⑶仅让电机在额定功率提供动力的情况下,当车速为v1=1.0m/s时,人骑车的加速度大小。
汽车的功率:汽车在行驶的过程中,发动机的最大功率等于额定功率。
P = F v
汽车功率(油门)
汽车的牵引力
汽车的瞬时速度
汽车加速运动的情况有两种:
1、以额定功率P启动;
2、在恒定的牵引力F作用下匀加速启动。
机车启动问题
汽车的功率中的几个物理量:
P额:额定功率 P:实际功率 F:牵引力
v:瞬时速度 F阻:阻力
G
F
FN
F阻
机车启动问题
类型1:机车以恒定功率 P 启动
思考:汽车在行驶时受到哪些力?
(P不变,F阻不变)
思考:随着汽车启动汽车速度如何变化?
汽车所受牵引力又是如何变化?如何判断?
汽车速度V逐渐增大
P = F v
v增大
P不变
F 减小
思考:汽车启动过程中加速度如何变化?如何判断?
由牛顿第二定律
F- F阻= ma
F 减小
F阻不变
a减小
思考:汽车启动过程中做什么运动?
加速度减小的加速直线运动
机车启动问题
类型1:机车以恒定功率 P 启动
思考:汽车加速度减到0之后做什么运动?
匀速直线运动
思考:汽车匀速时速度如何求解?
汽车匀速
a=0
F=F阻
P = F vm=F阻vm
G
F
FN
F阻
P
F阻
vm=
当F=F阻时,
a=0 ,v达到最大
保持
vm
匀速
v
F=
v
P
a=
m
F-F阻
↑
→
↓
↑
→
→
↓
↓
vm=
F阻
P
加速度逐渐减小的加速直线运动
匀速直线运动
类型1:机车以恒定功率 P 启动
机车启动问题
v- t 图像
机车启动问题
类型1:机车以恒定功率 P 启动
P- t 图像
F- t 图像
vm
v- t 图像
v
t
0
机车启动问题
类型1:机车以恒定功率 P 启动
P- t 图像
P
t
0
P
vm=
F阻
F
t
0
F- t 图像
F阻
[例1]汽车发动机的额定功率为60KW,汽车的质量为5t,汽车在水平路面上行驶时,阻力是车重的0.1倍,g=10m/s2。汽车保持额定功率不变从静止启动后:
①汽车所能达到的最大速度是多大?
②当汽车的速度为5m/s时加速度多大?
③当汽车的加速度为2m/s2时速度多大?
12m/s
4m/s
1.4m/s2
例题分析
[练习]一辆重5 t的汽车,发动机的额定功率为80 kW.汽车从静止开始以额定功率启动,车受的阻力为车重的0.06倍.(g取10 m/s2)求
(1) 汽车以额定功率做匀速运动的最终速度多大?
(2) 汽车速度为20 m/s时,加速度多大?
答案: (1)26.7 m/s (2)0.2 m/s2
机车启动问题
类型2:机车以恒定加速度 a 启动
(a不变,F阻不变)
G
F
FN
F阻
由牛顿第二定律
F- F阻= ma
F 不变
F阻不变
a不变
又:P = F v
F不变
V增大
P增大
思考:汽车输出功率P能否无限制增加?
不能,输出功率最大等于额定功率
当:P =P额
当汽车达到额定功率后功率P不变,回到类型1,以恒定功率运动。
机车启动问题
类型2:机车以恒定加速度 a 启动
当:P =P额=F v
v增大
P不变
F 减小
F- F阻= ma
F 减小
F阻不变
a减小
汽车匀速
a=0
F=F阻
P额 = F vm=F阻vm
P额
vm=
F阻
当F= F阻时,
a=0 ,v达到最大
保持
vm
匀速
F=
v
P额
a=
m
F-F阻
↑
→
↓
v
↑
↓
→
→
↓
vm=
F阻
P额
加速度逐渐减小的加速直线运动
匀速直线运动
a=
m
F-F阻
→
→
→
→
F
→
v
↑
P=F v
↑
↑
→
当P= P额时,保持P额继续加速
匀加速直线运动
类型2:机车以恒定加速度 a 启动
一、机车启动问题
v- t 图像
机车启动问题
P- t 图像
F- t 图像
类型2:机车以恒定加速度 a 启动
v
t
0
vm=
F阻
P额
vm
机车启动问题
类型2:机车以恒定加速度 a 启动
v- t 图像
P- t 图像
F- t 图像
P
t
0
P额
t1
t2
v1
t1
F
t
0
F=F阻+ma
t1
t2
F阻
P = F v=Fat
v
t
0
vm=
F阻
P额
vm
机车启动问题
类型2:机车以恒定加速度 a 启动
P
t
0
P额
t1
t2
v1
t1
F
t
0
F=F阻+ma
t1
t2
F阻
P = F v=Fat
思考:如何求解v1 、t1?
由牛顿第二定律
F- F阻= ma
F=F阻+ma
v1 :P=P额=FV1
v1=
F阻+ma
P额
t1=
a
V1
由V=V0+at
=
(F阻+ma)a
P额
1.没有达到最大速度时,有瞬时加速度。
2.达到最大速度时,a=0 F牵=f
注意:发动机的功率是指牵引力的功率而不是指合外力或阻力的功率。
汽车的两种运动状态
机车启动问题
[例2]汽车在水平路面以a=2m/s2,从静止启动做匀加速直线运动,汽车额定功率为80KW,汽车能达到的最大速度为20m/s,质量为2t,汽车在水平路面上行驶时,所受阻力不变,g=10m/s2。
①汽车所受阻力为多大?
②汽车匀加速运动的时间是多少?
③汽车3s末的速度多大?
④汽车速度为16m/s时末的加速度多大?
F阻=4000N
v=6m/s
t=5s
例题分析
a1=0.5m/s2
[练习2]水平面上静止放置一质量为m=0.2 kg 的物块,固定在同一水平面上的小型电动机通过水平细线牵引物块,使物块由静止开始做匀加速直线运动,2 s末达到额定功率,其v -t图线如图所示,物块与水平面间的动摩擦因数为μ=0.1,取g=10 m/s2,电动机与物块间的距离足够长.求:
(1)物块做匀加速直线运动时受到的牵引力大小;
(2)电动机的额定功率;
(3)物块在电动机牵引下,最终能达到的最大速度.
答案: (1)0.28 N
(2)0.224 W
(3)1.12 m/s
从P = Fv可以看出,汽车、火车等交通工具和各种起重机械,当发动机的输出功率P一定时,牵引力F与速度v成反比。你认为应该怎样增大它们的牵引力呢?
从P=Fv可以看出,汽车当发动机的功率P一定时,牵引力F与速度成反比,要增大牵引力,就要减小速度。
汽车的输出功率
汽车的牵引力
汽车的瞬时速度
(油门)
发动机输出的功率不能无限制地增大,所以汽车上坡时,司机要用“换挡”的办法减小速度,来得到较大的牵引力。
不过,在发动机功率一定时,通过减小速度提高牵引力或通过减小牵引力而提高速度,效果都是有限的。所以,要提高速度和增大牵引力,必须提高发动机的额定功率,这就是高速火车、汽车和大型舰船需要大功率发动机的原因。
