等腰三角形的性质课件.[上学期]
文档属性
| 名称 | 等腰三角形的性质课件.[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 323.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-11-15 00:00:00 | ||
图片预览



文档简介
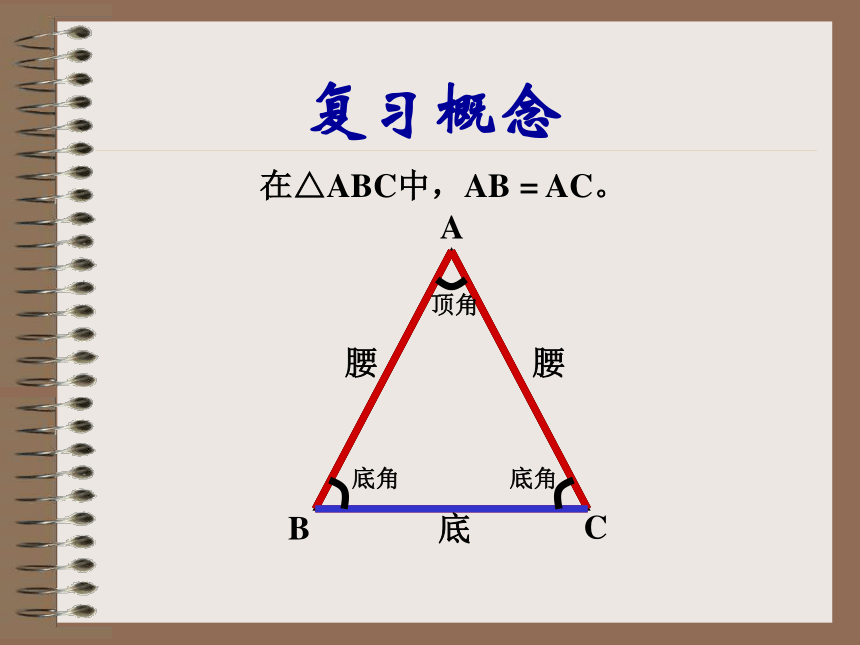
课件21张PPT。14.3.1等腰三角形的性质古南中学 罗昭强复习概念底顶角等腰三角形在实际生活中的应用等腰三角形等腰三角形的性质:
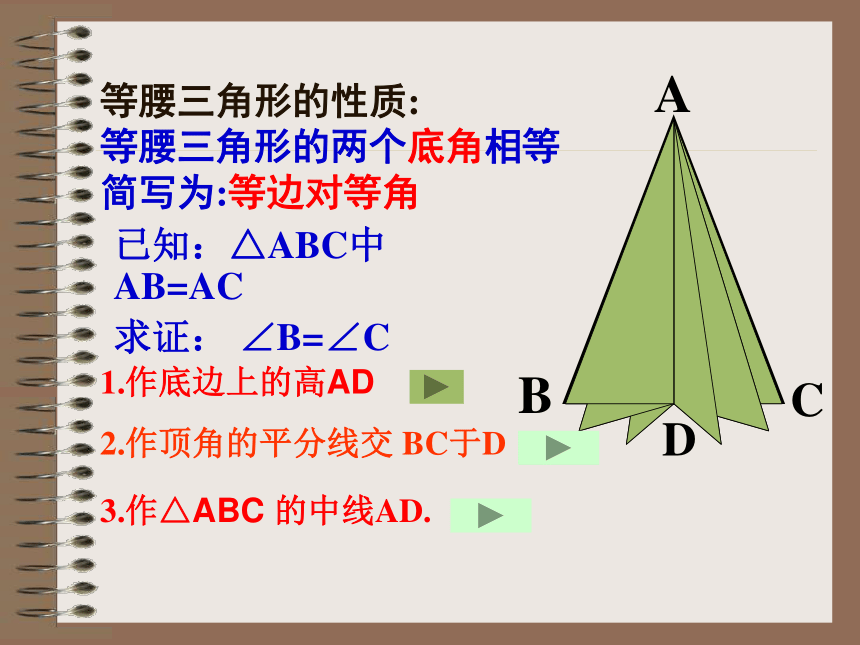
等腰三角形的两个底角相等
简写为:等边对等角已知:△ABC中 AB=AC
求证: ∠B=∠C
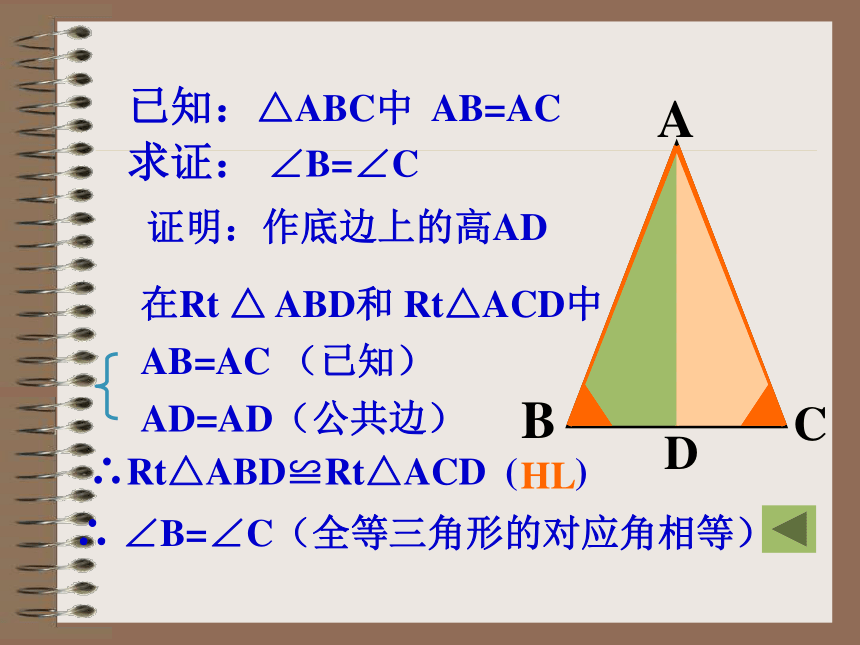
2.作顶角的平分线交 BC于D1.作底边上的高AD 3.作△ABC 的中线AD.证明:作底边上的高AD ∴Rt△ABD≌Rt△ACD ( ) ∴ ∠B=∠C(全等三角形的对应角相等)已知:△ABC中 AB=AC
求证: ∠B=∠C
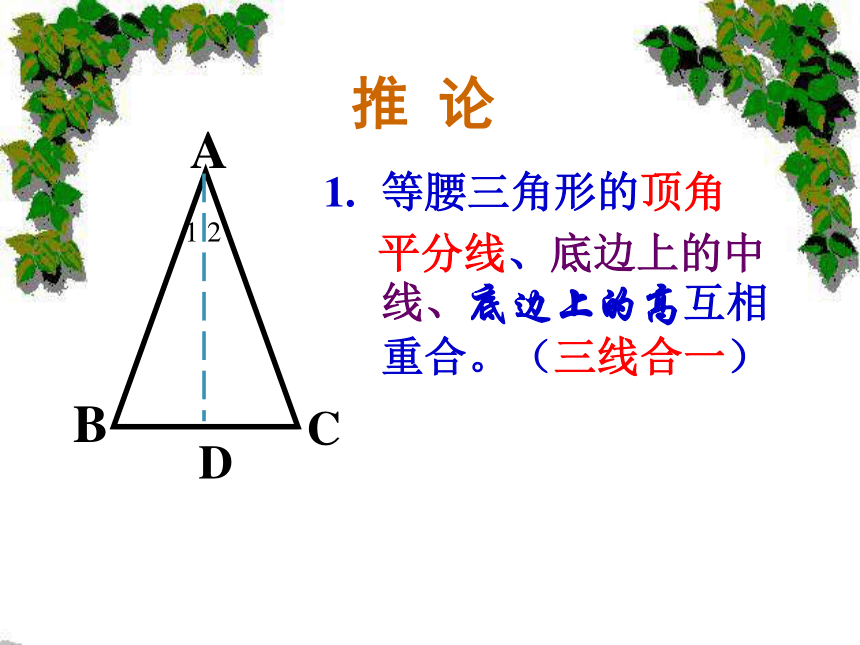
AB=AC (已知)AD=AD(公共边)HL在Rt △ ABD和 Rt△ACD中推 论等腰三角形的顶角
平分线、底边上的中线、底边上的高互相重合。(三线合一)填空:在△ABC中
(1) ∵ AB=AC ,
∴∠__=∠__
D(2) ∵ AB=AC ,AD是角平分线,
∴ ⊥ , = __.(3) ∵ AB=AC,AD是中线,
∴ ⊥ ,∠_=∠_.(4) ∵ AB=AC,AD 是高,
∴ __ = __,
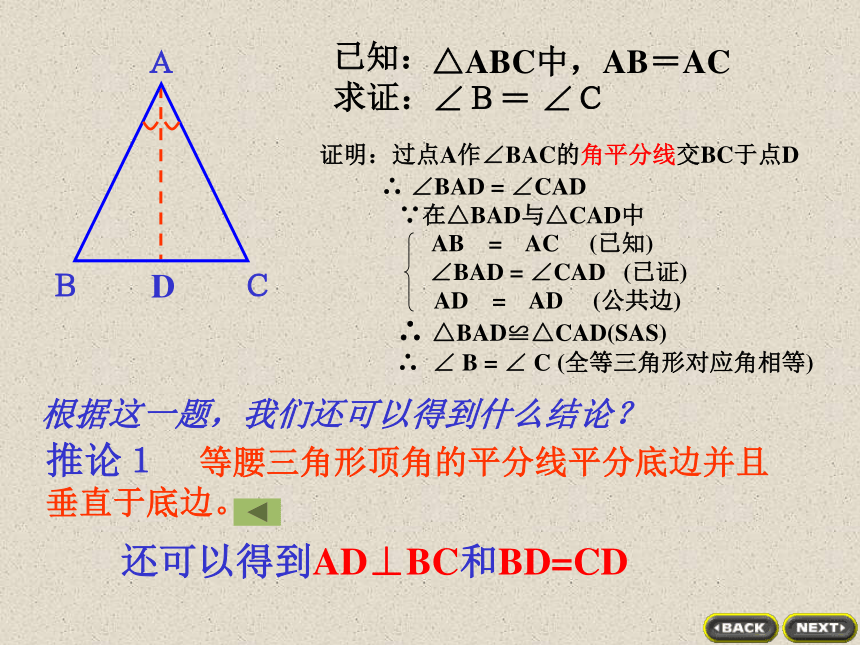
∠__=∠__.性质及推论的推理格式证明:过点A作∠BAC的角平分线交BC于点D
D根据这一题,我们还可以得到什么结论?还可以得到AD⊥BC和BD=CD推论1 等腰三角形顶角的平分线平分底边并且
垂直于底边。△ABC中,AB=AC∠B= ∠CABC已知:△ABC中,AB=AC
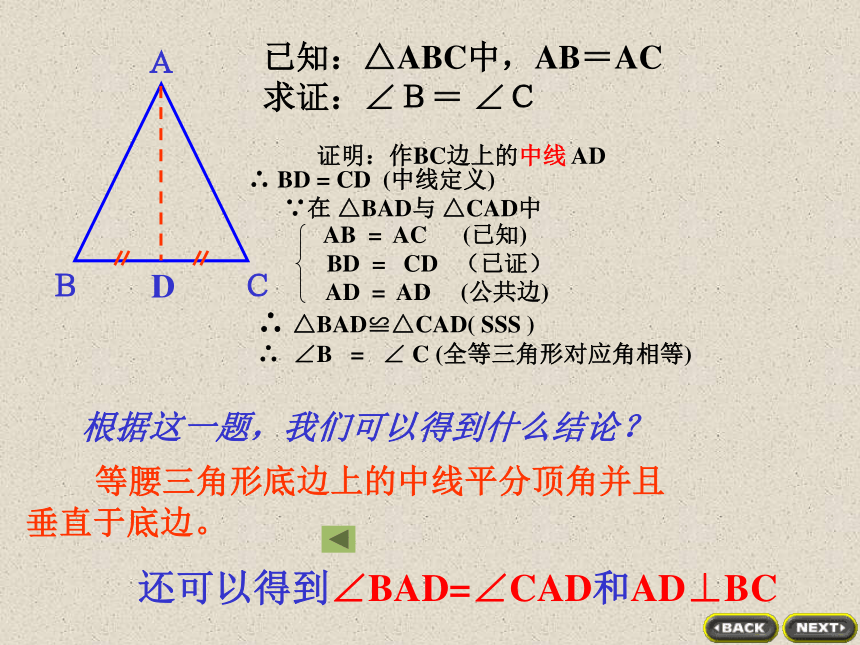
求证:∠B= ∠C证明:作BC边上的中线 AD
D还可以得到∠BAD=∠CAD和AD⊥BC根据这一题,我们可以得到什么结论? 等腰三角形底边上的中线平分顶角并且
垂直于底边。AC已知:△ABC中,AB=AC
求证:∠B= ∠C证明:过点A作AD⊥BC交BC于点D
DB还可以得到∠BAD=∠CAD和BD=CD根据这一题,我们还可以得什么结论? 等腰三角形底边上的高平分底边并且平分顶角。(不能)找出下面图形中相等的角:(1)在△ABC中,AC=BC, ∠ACB=90°,CD⊥AB∠A=∠B=∠ACD=∠BCD=45°∠ADC=∠BDC=∠ACB=90°巩固练习一巩固练习二根据下列条件求等腰三角形中其余角的度数顶角为70°
(2)一个底角为45 °(3)一个底角为60 °(4)一个角是30 °(5)一个外角是70 °55 °和55 °45 °和90 °60 °和60 °30 °和120 °或75 °和75 °110 °、35 °、35 °巩固练习三在△ABC中, AB=AC=BC, 用已有的知识。如何推导出∠A、∠B、∠C的度数。证明:∵AB = AC
∴∠B = ∠C (等边对等角)
同理: ∠A = ∠ C、 ∠A= ∠B
∴ ∠B = ∠C = ∠A
∴ ∠B = ∠C = ∠A = 60°∵∠B + ∠C + ∠A =180°(三角形内角和定理)巩固练习已知:在△ABC中,AB=AC,CD⊥AB,∠1=45°
求: ∠BCD的度数例:如图,在△ABC中,AB=AC,,点D在AC上,且BD=BC=AD, 1)找出图中相等的角 2)求△ABC各角的度数.(自己作)小结等腰三角形性质等腰三角形三线合一等边对等角等边三角形各边都相等练一练:已知:如图,房屋的顶角∠BAC = 100°,过屋顶 A的立柱AD ⊥ BC,屋椽AB = AC。
求:顶架上∠B、 ∠C、 ∠BAD、 ∠CAD的度数。解:在△ABC中,
∵AB = AC (已知)
∴∠B = ∠C(等边对等角)
∴∠B = ∠C =
(180°—∠BAC) = 40 °(三角形内角和定理)
又∵AD ⊥ BC (已知)
∴∠BAD = ∠CAD ( )∴∠BAD = ∠CAD = 50°三线合一) 已知:AD = DC=CB,∠A= 25° 求:∠DCB的度数。考考你思考:等腰三角形底边中点到两腰的距离相等吗?能说明理由吗?布置作业名校课堂:第52页 14.3.1一课时
课外作业:教科书:143页练习,做在书上
求证: ∠B=∠C
2.作顶角的平分线交 BC于D1.作底边上的高AD 3.作△ABC 的中线AD.证明:作底边上的高AD ∴Rt△ABD≌Rt△ACD ( ) ∴ ∠B=∠C(全等三角形的对应角相等)已知:△ABC中 AB=AC
求证: ∠B=∠C
AB=AC (已知)AD=AD(公共边)HL在Rt △ ABD和 Rt△ACD中推 论等腰三角形的顶角
平分线、底边上的中线、底边上的高互相重合。(三线合一)填空:在△ABC中
(1) ∵ AB=AC ,
∴∠__=∠__
D(2) ∵ AB=AC ,AD是角平分线,
∴ ⊥ , = __.(3) ∵ AB=AC,AD是中线,
∴ ⊥ ,∠_=∠_.(4) ∵ AB=AC,AD 是高,
∴ __ = __,
∠__=∠__.性质及推论的推理格式证明:过点A作∠BAC的角平分线交BC于点D
D根据这一题,我们还可以得到什么结论?还可以得到AD⊥BC和BD=CD推论1 等腰三角形顶角的平分线平分底边并且
垂直于底边。△ABC中,AB=AC∠B= ∠CABC已知:△ABC中,AB=AC
求证:∠B= ∠C证明:作BC边上的中线 AD
D还可以得到∠BAD=∠CAD和AD⊥BC根据这一题,我们可以得到什么结论? 等腰三角形底边上的中线平分顶角并且
垂直于底边。AC已知:△ABC中,AB=AC
求证:∠B= ∠C证明:过点A作AD⊥BC交BC于点D
DB还可以得到∠BAD=∠CAD和BD=CD根据这一题,我们还可以得什么结论? 等腰三角形底边上的高平分底边并且平分顶角。(不能)找出下面图形中相等的角:(1)在△ABC中,AC=BC, ∠ACB=90°,CD⊥AB∠A=∠B=∠ACD=∠BCD=45°∠ADC=∠BDC=∠ACB=90°巩固练习一巩固练习二根据下列条件求等腰三角形中其余角的度数顶角为70°
(2)一个底角为45 °(3)一个底角为60 °(4)一个角是30 °(5)一个外角是70 °55 °和55 °45 °和90 °60 °和60 °30 °和120 °或75 °和75 °110 °、35 °、35 °巩固练习三在△ABC中, AB=AC=BC, 用已有的知识。如何推导出∠A、∠B、∠C的度数。证明:∵AB = AC
∴∠B = ∠C (等边对等角)
同理: ∠A = ∠ C、 ∠A= ∠B
∴ ∠B = ∠C = ∠A
∴ ∠B = ∠C = ∠A = 60°∵∠B + ∠C + ∠A =180°(三角形内角和定理)巩固练习已知:在△ABC中,AB=AC,CD⊥AB,∠1=45°
求: ∠BCD的度数例:如图,在△ABC中,AB=AC,,点D在AC上,且BD=BC=AD, 1)找出图中相等的角 2)求△ABC各角的度数.(自己作)小结等腰三角形性质等腰三角形三线合一等边对等角等边三角形各边都相等练一练:已知:如图,房屋的顶角∠BAC = 100°,过屋顶 A的立柱AD ⊥ BC,屋椽AB = AC。
求:顶架上∠B、 ∠C、 ∠BAD、 ∠CAD的度数。解:在△ABC中,
∵AB = AC (已知)
∴∠B = ∠C(等边对等角)
∴∠B = ∠C =
(180°—∠BAC) = 40 °(三角形内角和定理)
又∵AD ⊥ BC (已知)
∴∠BAD = ∠CAD ( )∴∠BAD = ∠CAD = 50°三线合一) 已知:AD = DC=CB,∠A= 25° 求:∠DCB的度数。考考你思考:等腰三角形底边中点到两腰的距离相等吗?能说明理由吗?布置作业名校课堂:第52页 14.3.1一课时
课外作业:教科书:143页练习,做在书上
