等腰三角形判定1[上学期]
文档属性
| 名称 | 等腰三角形判定1[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 353.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-11-15 00:00:00 | ||
图片预览


文档简介
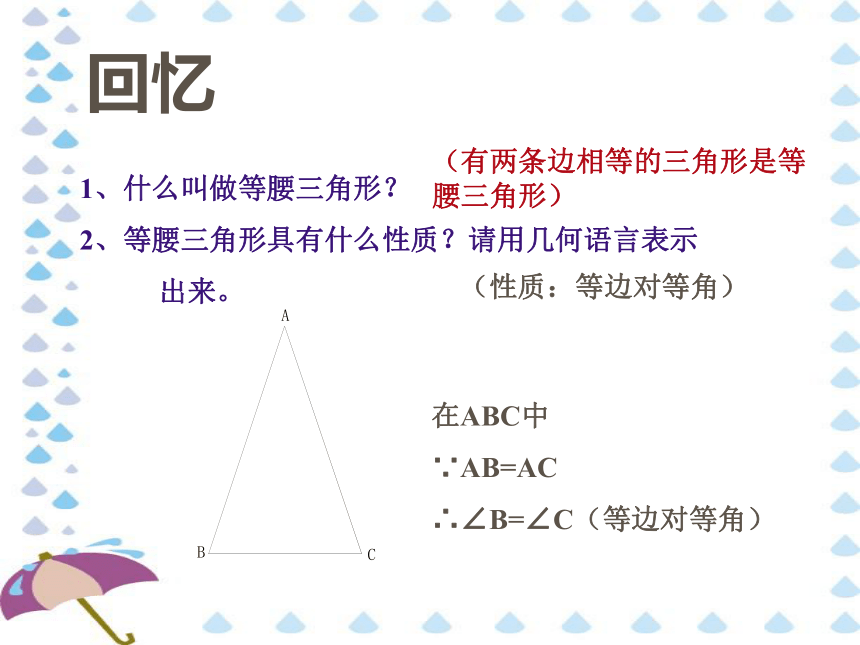
课件14张PPT。古南中学 罗昭强等腰三角形的判定1回忆1、什么叫做等腰三角形?
2、等腰三角形具有什么性质?请用几何语言表示
出来。在ABC中
∵AB=AC
∴∠B=∠C(等边对等角)(有两条边相等的三角形是等 腰三角形)(性质:等边对等角)等腰三角形的判定如果一个三角形有两个角相等,那么这两个角所对的边也相等。发现:简称:等角对等边在△ABC中
∵∠B=∠C
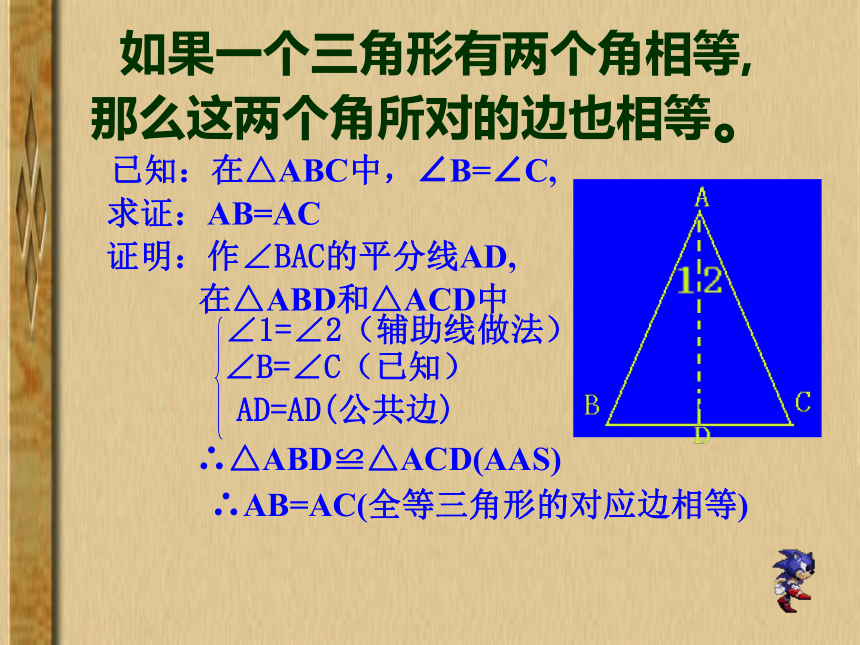
∴AB=AC(等角对等边)定理如果一个三角形有两个角相等,
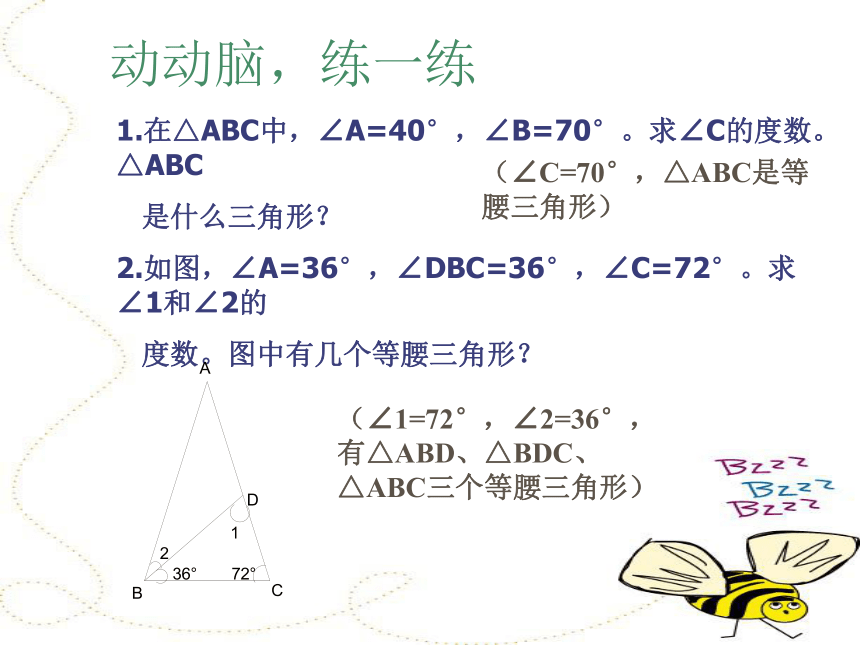
那么这两个角所对的边也相等。证明:作∠BAC的平分线AD,已知:在△ABC中,∠B=∠C,求证:AB=AC在△ABD和△ACD中∠1=∠2(辅助线做法)∠B=∠C(已知)AD=AD(公共边)∴△ABD≌△ACD(AAS)∴AB=AC(全等三角形的对应边相等) 动动脑,练一练1.在△ABC中,∠A=40°,∠B=70°。求∠C的度数。△ABC
是什么三角形?
2.如图,∠A=36°,∠DBC=36°,∠C=72°。求∠1和∠2的
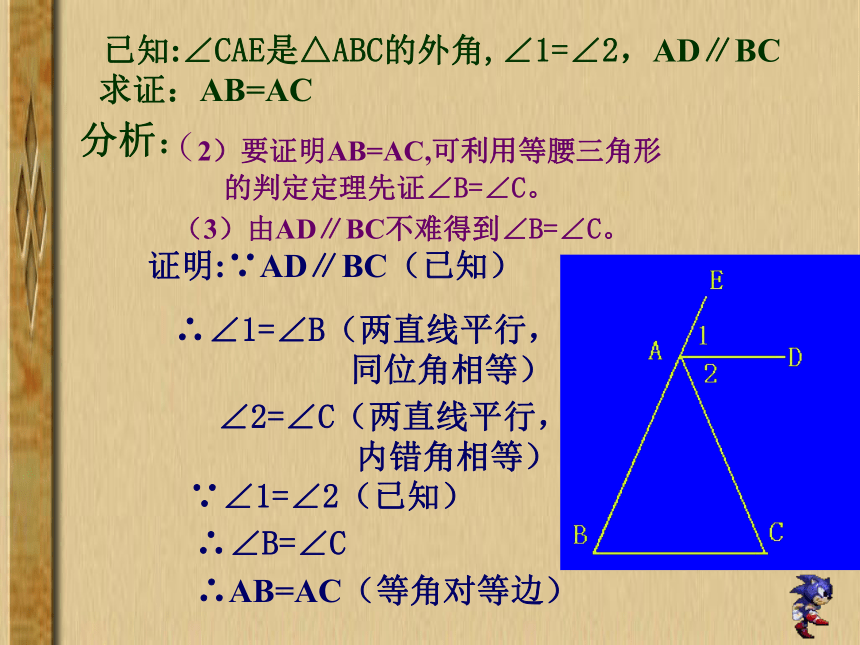
度数。图中有几个等腰三角形?(∠C=70°,△ABC是等腰三角形)(∠1=72°,∠2=36°,有△ABD、△BDC、△ABC三个等腰三角形)(2)要证明AB=AC,可利用等腰三角形
的判定定理先证∠B=∠C。(3)由AD∥BC不难得到∠B=∠C。已知:∠CAE是△ABC的外角,∠1=∠2,AD∥BC求证:AB=AC证明:∵AD∥BC(已知)∴∠1=∠B(两直线平行,
同位角相等)∠2=∠C(两直线平行,
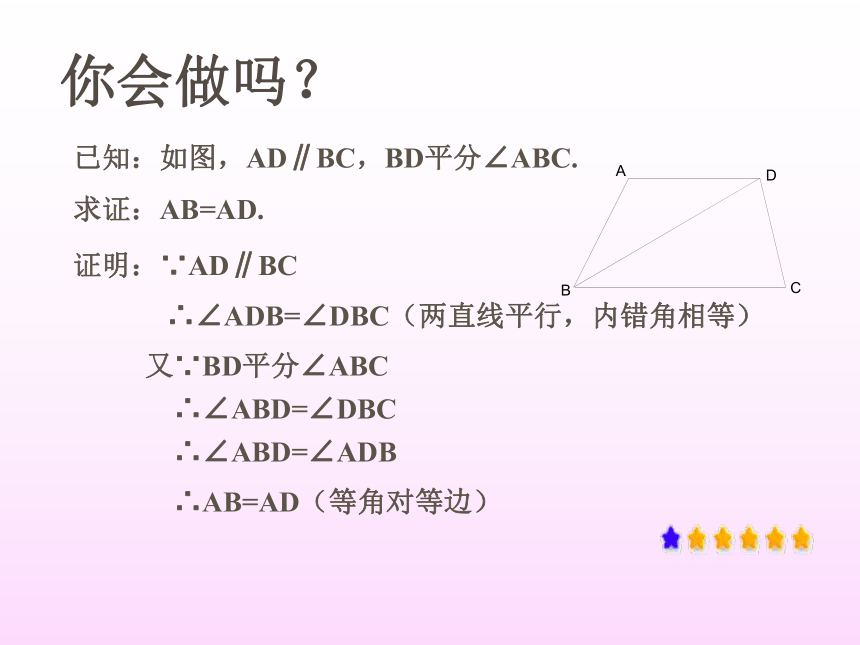
内错角相等)∵∠1=∠2(已知)∴∠B=∠C∴AB=AC(等角对等边)分析:你会做吗?已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.证明:∵AD∥BC∴∠ADB=∠DBC(两直线平行,内错角相等)又∵BD平分∠ABC∴∠ABD=∠DBC∴∠ABD=∠ADB∴AB=AD(等角对等边)已知:如图,AD∥BC,BD平分∠ABC.
探 究1、若AD=4cm,则AB=( )cm.2、若延长BA、CD交于点E,AE=5cm,则BE=( )cm.49E已知:如图,BI平分∠ABC,CI平分∠ACB,
DE经过点I,且DE∥BC.求证:△ADE的周长=AB+AC分析:△ADE的周长=AD+DE+AEDI+IEBDEC深 入于是 △ADE的周长=AD+BD+EC+AE
=AB+AC课外思考如图,在Rt△ABC中,∠C=90°,∠A=30°,D为AB上一点,且BD=BC. 仔细观察,图中有几组线段相等?有等腰三角形吗?
想一想,是否具备这些条件的直角三角形一定有这样的结论?
你能发现BC和AB之间的关系吗?2.如图,已知∠A=360 ,∠DBC=360,
∠C=720。计算∠1和∠2的度数。 并说明图中有哪些等腰三角形? 课堂练习内容回顾1、等腰三角形的判定定理 ——等角对等边。
2、等腰三角形的判定定理的两个推论。
3、等腰三角形的判定定理和性质定理是一对互逆定理。
4、等腰三角形的判定定理是证明线段相等的一种重要 的方法。 作业:再见
2、等腰三角形具有什么性质?请用几何语言表示
出来。在ABC中
∵AB=AC
∴∠B=∠C(等边对等角)(有两条边相等的三角形是等 腰三角形)(性质:等边对等角)等腰三角形的判定如果一个三角形有两个角相等,那么这两个角所对的边也相等。发现:简称:等角对等边在△ABC中
∵∠B=∠C
∴AB=AC(等角对等边)定理如果一个三角形有两个角相等,
那么这两个角所对的边也相等。证明:作∠BAC的平分线AD,已知:在△ABC中,∠B=∠C,求证:AB=AC在△ABD和△ACD中∠1=∠2(辅助线做法)∠B=∠C(已知)AD=AD(公共边)∴△ABD≌△ACD(AAS)∴AB=AC(全等三角形的对应边相等) 动动脑,练一练1.在△ABC中,∠A=40°,∠B=70°。求∠C的度数。△ABC
是什么三角形?
2.如图,∠A=36°,∠DBC=36°,∠C=72°。求∠1和∠2的
度数。图中有几个等腰三角形?(∠C=70°,△ABC是等腰三角形)(∠1=72°,∠2=36°,有△ABD、△BDC、△ABC三个等腰三角形)(2)要证明AB=AC,可利用等腰三角形
的判定定理先证∠B=∠C。(3)由AD∥BC不难得到∠B=∠C。已知:∠CAE是△ABC的外角,∠1=∠2,AD∥BC求证:AB=AC证明:∵AD∥BC(已知)∴∠1=∠B(两直线平行,
同位角相等)∠2=∠C(两直线平行,
内错角相等)∵∠1=∠2(已知)∴∠B=∠C∴AB=AC(等角对等边)分析:你会做吗?已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.证明:∵AD∥BC∴∠ADB=∠DBC(两直线平行,内错角相等)又∵BD平分∠ABC∴∠ABD=∠DBC∴∠ABD=∠ADB∴AB=AD(等角对等边)已知:如图,AD∥BC,BD平分∠ABC.
探 究1、若AD=4cm,则AB=( )cm.2、若延长BA、CD交于点E,AE=5cm,则BE=( )cm.49E已知:如图,BI平分∠ABC,CI平分∠ACB,
DE经过点I,且DE∥BC.求证:△ADE的周长=AB+AC分析:△ADE的周长=AD+DE+AEDI+IEBDEC深 入于是 △ADE的周长=AD+BD+EC+AE
=AB+AC课外思考如图,在Rt△ABC中,∠C=90°,∠A=30°,D为AB上一点,且BD=BC. 仔细观察,图中有几组线段相等?有等腰三角形吗?
想一想,是否具备这些条件的直角三角形一定有这样的结论?
你能发现BC和AB之间的关系吗?2.如图,已知∠A=360 ,∠DBC=360,
∠C=720。计算∠1和∠2的度数。 并说明图中有哪些等腰三角形? 课堂练习内容回顾1、等腰三角形的判定定理 ——等角对等边。
2、等腰三角形的判定定理的两个推论。
3、等腰三角形的判定定理和性质定理是一对互逆定理。
4、等腰三角形的判定定理是证明线段相等的一种重要 的方法。 作业:再见
