等腰三角形的性质公开课[上学期]
文档属性
| 名称 | 等腰三角形的性质公开课[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 802.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-11-27 00:00:00 | ||
图片预览


文档简介
课件22张PPT。等腰三角形的性质
讲课人:贺诗平 等腰三角形的相关概念
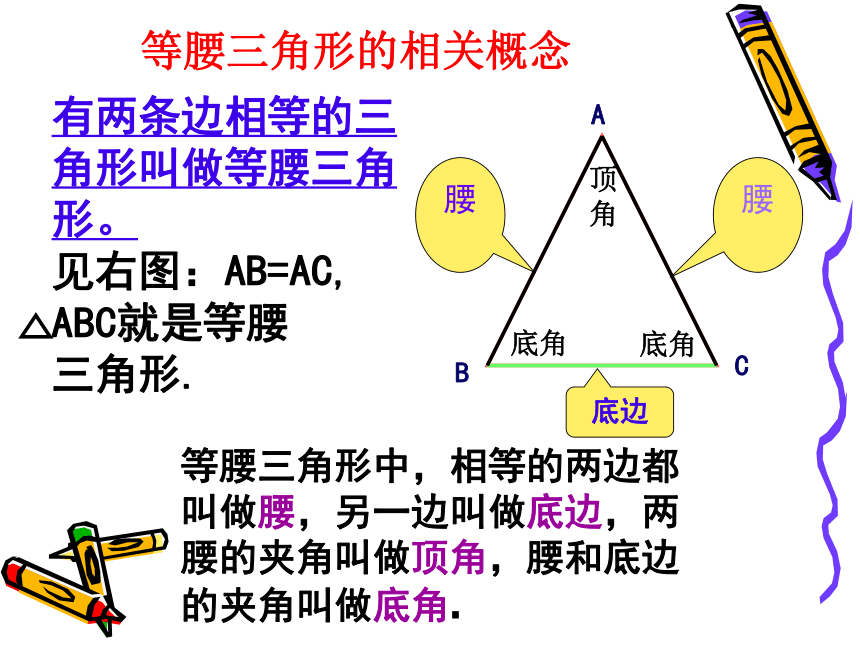
底边等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.有两条边相等的三角形叫做等腰三角形。
见右图:AB=AC, ABC就是等腰
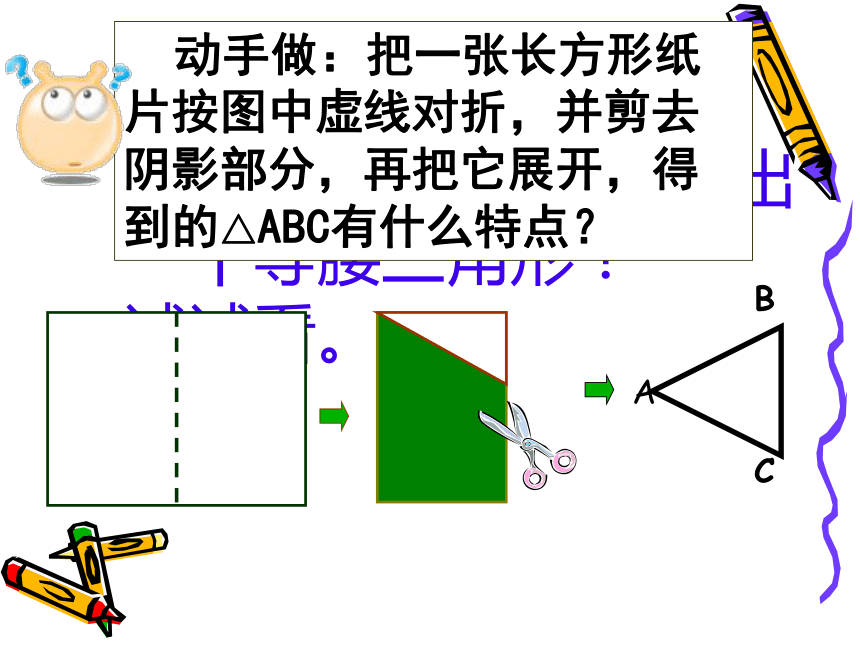
三角形. 用折纸的方法能否折出 一个等腰三角形? 试试看。 动手做:把一张长方形纸片按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?
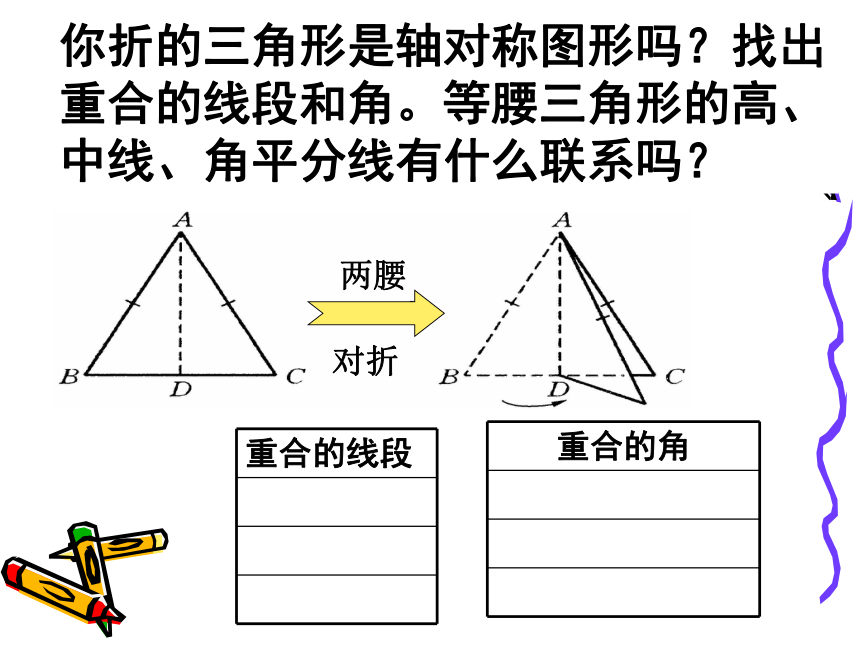
你折的三角形是轴对称图形吗?找出重合的线段和角。等腰三角形的高、中线、角平分线有什么联系吗?
你折的三角形是轴对称图形吗?找出重合的线段和角。等腰三角形的高、中线、角平分线有什么联系吗?
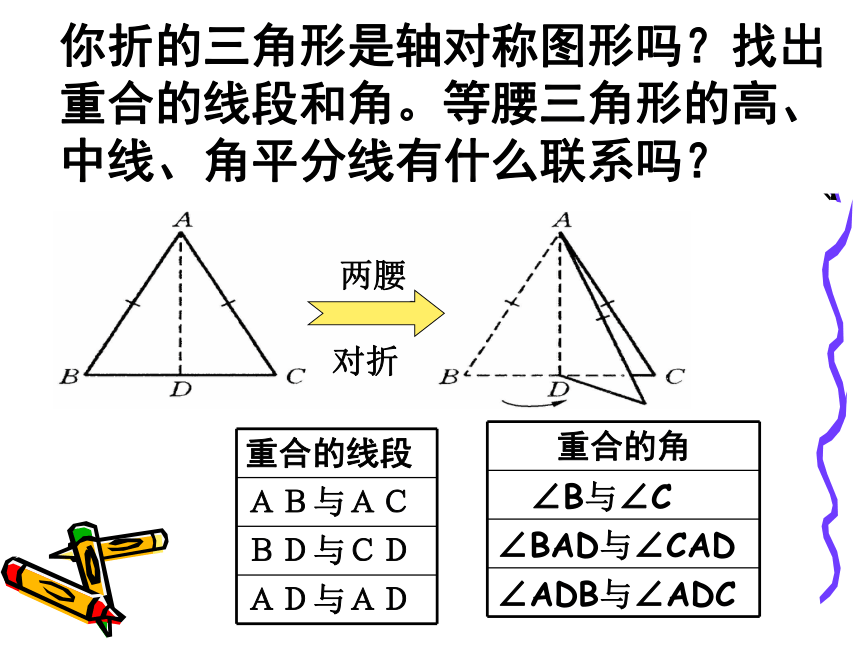
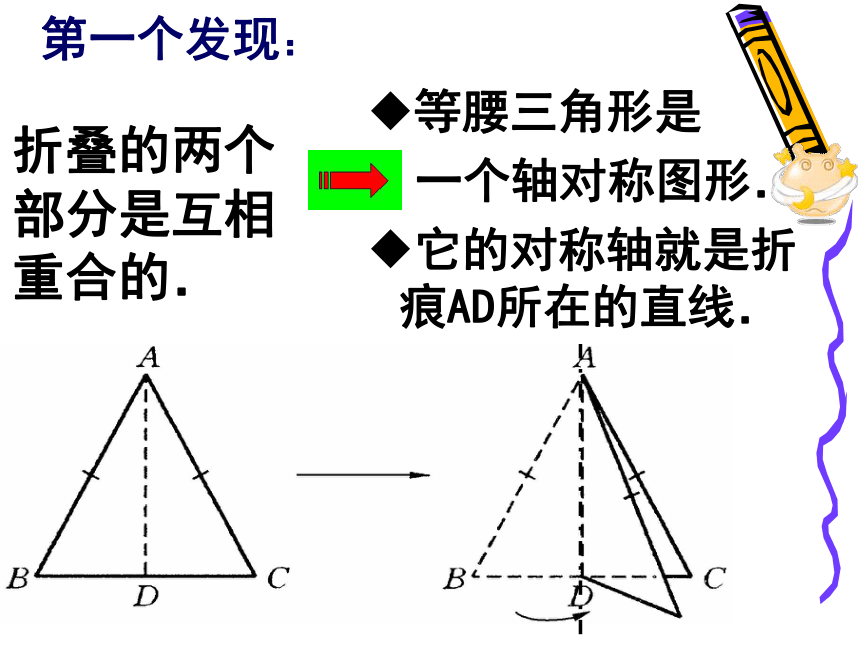
第一个发现:折叠的两个部分是互相重合的.等腰三角形是
一个轴对称图形.
它的对称轴就是折痕AD所在的直线.
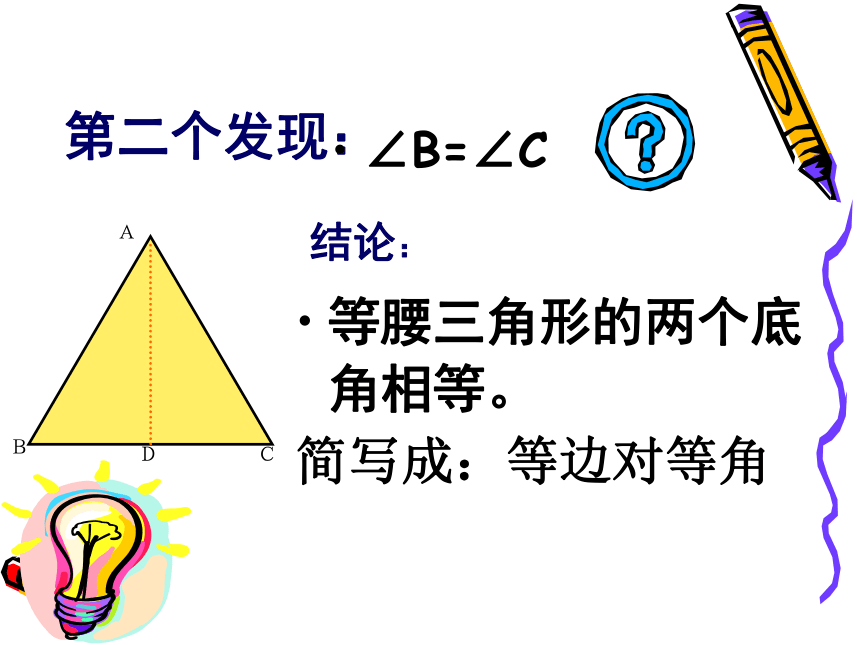
第二个发现:∠B=∠C结论:等腰三角形的两个底角相等。
简写成:等边对等角
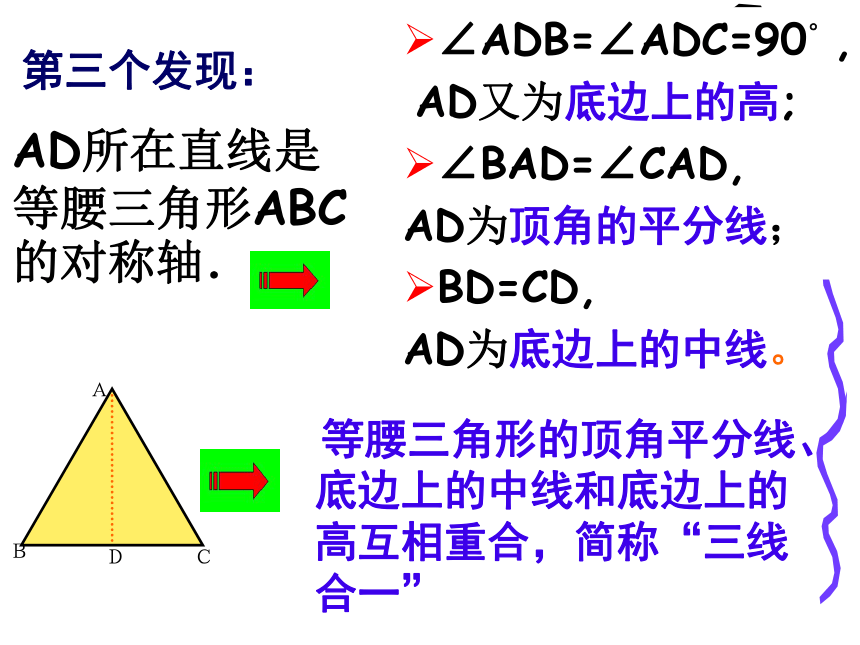
第三个发现:AD所在直线是等腰三角形ABC的对称轴.∠ADB=∠ADC=90°,
AD又为底边上的高;
∠BAD=∠CAD,
AD为顶角的平分线;
BD=CD,
AD为底边上的中线。
等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合,简称“三线合一”
2.等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合,简称“三线合一”.1.等腰三角形的两个底角相等。
(等边对等角)现在和你同伴讨论一下如何证明等腰三角形的性质,有几种方法?你总结出等腰三角形的性质是什么?性质1的证明性质2的证明自学课本 142例1 学以致用 猜猜看,等腰三角形底边中点到两腰的距离相等吗?你可以将等腰三角形沿对称轴AD折叠,观察DE与DF的关系。
讨论EA如果DE、DF分别是AB、AC上的中线或∠ADB、∠ADC 的平分线,它们还相等吗?
由等腰三角形是轴对称图形,还能得到等腰三角形中哪些线段相等?(只要在三角形中就行)
由刚才的结论思考并讨论
下面我们回忆一下 今天所学的内容 课本143页,做练习3,P150第8.
熟能生巧!我们今天 的作业是:P149页,习题1. 4. 6再见 例:已知:如图AB=AC , AD⊥BC,∠BAC=90 。
求∠B、∠C、∠BAD、∠CAD的度数。图中有哪些相等的线段?ABCD应用举例○返回1.等腰三角形的一个角是36度,它的另外两个角是____.
2.等腰三角形的一个角是110度,它的另外两个角是____.返回
D性质1:等腰三角形的两个
底角相等。简写成:等边对等角返回CBA方法作辅助线顶角的角平分线作辅助线底边上的高作辅助线底边上的中线DCBA返回已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作顶角的平分线AD 在ΔBAD和ΔCAD中AB=AC(已知)∠1=∠2(辅助线作法)AD=AD(公共边)∴ ΔBAD ≌ΔCAD(SAS)∴ ∠B=∠C(全等三角形的对应角相等)性质1:等腰三角形的两个底角相等。简写成:等边对等角等腰三角形
性质的证明返回已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作底边上中线AD 在ΔBAD和ΔCAD中AB=AC(已知)BD=CD(辅助线作法)AD=AD(公共边)∴ ΔBAD ≌ΔCAD(SSS)∴ ∠B=∠C(全等三角形的对应角相等)性质1:等腰三角形的两个底角相等。简写成:等边对等角等腰三角形
性质的证明返回已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作底边上的高AD 在RtΔBAD和RtΔCAD中AB=AC(已知)AD=AD(公共边)∴ Rt ΔBAD ≌ Rt ΔCAD(HL)∴ ∠B=∠C(全等三角形的对应角相等)性质1:等腰三角形的两个底角相等。简写成:等边对等角等腰三角形
性质的证明返回性质2:等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合,简称“三线合一”
DCBA方法:作BC边上的高AD,证明BC边上的中线和顶角的平分线和高是相互重合即可.返回
底边等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.有两条边相等的三角形叫做等腰三角形。
见右图:AB=AC, ABC就是等腰
三角形. 用折纸的方法能否折出 一个等腰三角形? 试试看。 动手做:把一张长方形纸片按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?
你折的三角形是轴对称图形吗?找出重合的线段和角。等腰三角形的高、中线、角平分线有什么联系吗?
你折的三角形是轴对称图形吗?找出重合的线段和角。等腰三角形的高、中线、角平分线有什么联系吗?
第一个发现:折叠的两个部分是互相重合的.等腰三角形是
一个轴对称图形.
它的对称轴就是折痕AD所在的直线.
第二个发现:∠B=∠C结论:等腰三角形的两个底角相等。
简写成:等边对等角
第三个发现:AD所在直线是等腰三角形ABC的对称轴.∠ADB=∠ADC=90°,
AD又为底边上的高;
∠BAD=∠CAD,
AD为顶角的平分线;
BD=CD,
AD为底边上的中线。
等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合,简称“三线合一”
2.等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合,简称“三线合一”.1.等腰三角形的两个底角相等。
(等边对等角)现在和你同伴讨论一下如何证明等腰三角形的性质,有几种方法?你总结出等腰三角形的性质是什么?性质1的证明性质2的证明自学课本 142例1 学以致用 猜猜看,等腰三角形底边中点到两腰的距离相等吗?你可以将等腰三角形沿对称轴AD折叠,观察DE与DF的关系。
讨论EA如果DE、DF分别是AB、AC上的中线或∠ADB、∠ADC 的平分线,它们还相等吗?
由等腰三角形是轴对称图形,还能得到等腰三角形中哪些线段相等?(只要在三角形中就行)
由刚才的结论思考并讨论
下面我们回忆一下 今天所学的内容 课本143页,做练习3,P150第8.
熟能生巧!我们今天 的作业是:P149页,习题1. 4. 6再见 例:已知:如图AB=AC , AD⊥BC,∠BAC=90 。
求∠B、∠C、∠BAD、∠CAD的度数。图中有哪些相等的线段?ABCD应用举例○返回1.等腰三角形的一个角是36度,它的另外两个角是____.
2.等腰三角形的一个角是110度,它的另外两个角是____.返回
D性质1:等腰三角形的两个
底角相等。简写成:等边对等角返回CBA方法作辅助线顶角的角平分线作辅助线底边上的高作辅助线底边上的中线DCBA返回已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作顶角的平分线AD 在ΔBAD和ΔCAD中AB=AC(已知)∠1=∠2(辅助线作法)AD=AD(公共边)∴ ΔBAD ≌ΔCAD(SAS)∴ ∠B=∠C(全等三角形的对应角相等)性质1:等腰三角形的两个底角相等。简写成:等边对等角等腰三角形
性质的证明返回已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作底边上中线AD 在ΔBAD和ΔCAD中AB=AC(已知)BD=CD(辅助线作法)AD=AD(公共边)∴ ΔBAD ≌ΔCAD(SSS)∴ ∠B=∠C(全等三角形的对应角相等)性质1:等腰三角形的两个底角相等。简写成:等边对等角等腰三角形
性质的证明返回已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作底边上的高AD 在RtΔBAD和RtΔCAD中AB=AC(已知)AD=AD(公共边)∴ Rt ΔBAD ≌ Rt ΔCAD(HL)∴ ∠B=∠C(全等三角形的对应角相等)性质1:等腰三角形的两个底角相等。简写成:等边对等角等腰三角形
性质的证明返回性质2:等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合,简称“三线合一”
DCBA方法:作BC边上的高AD,证明BC边上的中线和顶角的平分线和高是相互重合即可.返回
