14.3.1等腰三角形(1)[上学期]
文档属性
| 名称 | 14.3.1等腰三角形(1)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 719.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-11-28 09:55:00 | ||
图片预览

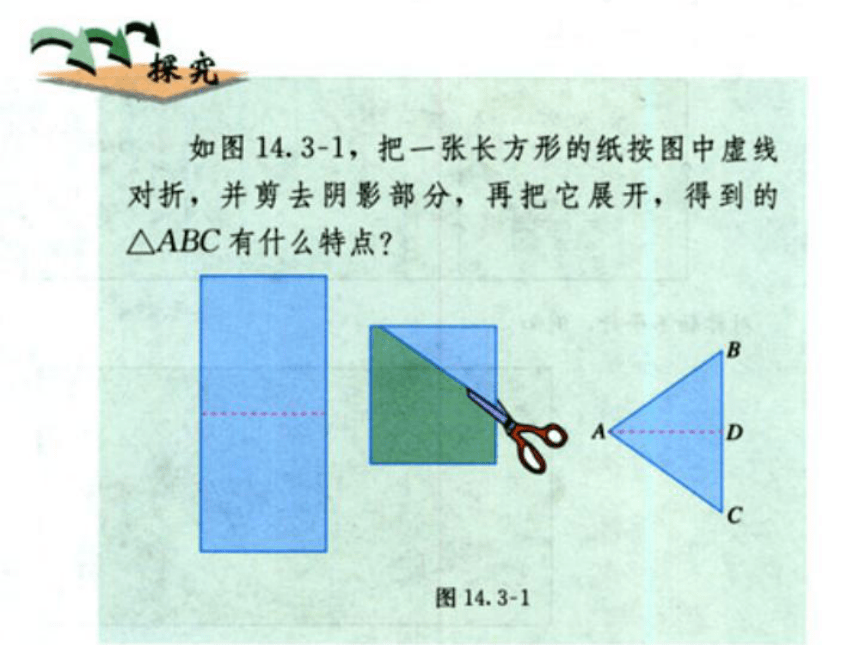





文档简介
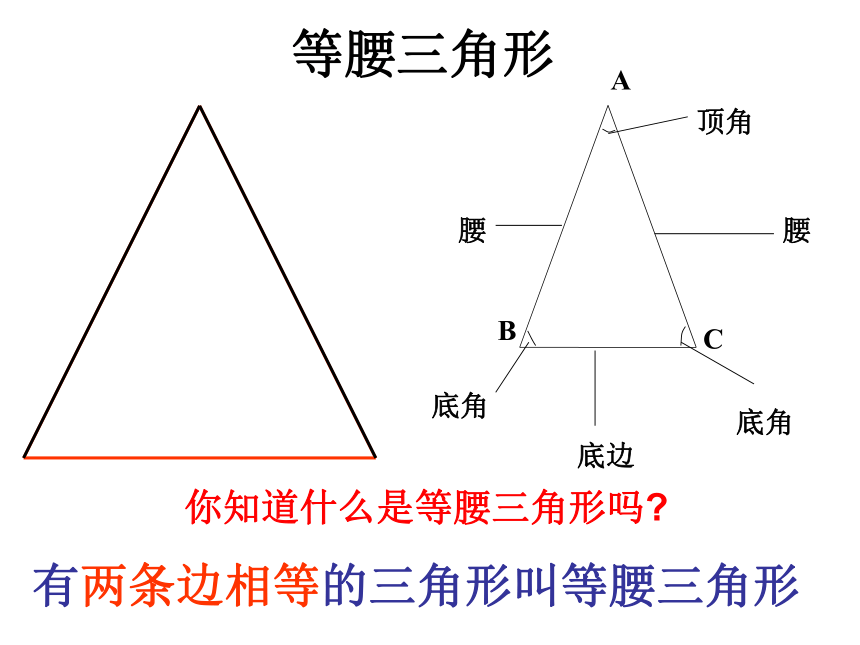
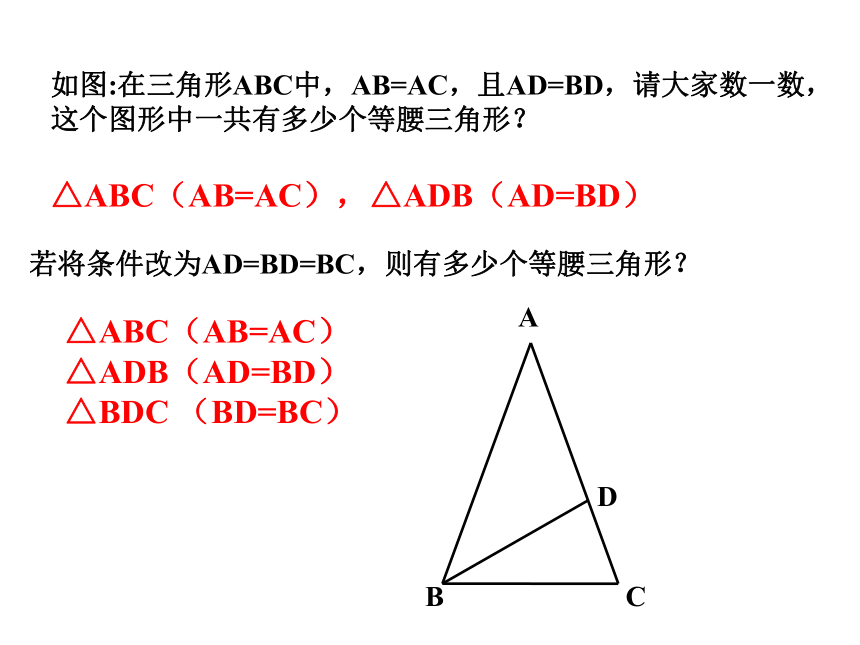
课件23张PPT。14.3.1 等腰三角形(1)温岭市泽国三中 莫勤方第十四章 轴对称等腰三角形你知道什么是等腰三角形吗?有两条边相等的三角形叫等腰三角形如图:在三角形ABC中,AB=AC,且AD=BD,请大家数一数,这个图形中一共有多少个等腰三角形?△ABC(AB=AC),△ADB(AD=BD)若将条件改为AD=BD=BC,则有多少个等腰三角形?△ABC(AB=AC)
△ADB(AD=BD)
△BDC (BD=BC)大胆猜测等腰三角形除了两腰相等以外,你还能发现什么?等腰三角形的两个底角相等。等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合等腰三角形是轴对称图形.CAB 命题: 等腰三角形的两个底角相等证明:作底边上的高AD ∴Rt△ABD≌Rt△ACD ( ) ∴ ∠B=∠C(全等三角形的对应角相等)已知:△ABC中 AB=AC
求证: ∠B=∠C
AB=AC (已知)AD=AD(公共边)HL在Rt △ ABD和 Rt△ACD中 在△ABD和 △ACD中
AB=AC (已知)
∠1=∠2(辅助线作法)
AD=AD(公共边) ∴△ABD≌△ACD(SAS) ∴ ∠B=∠C(全等三角形的对应角相等)已知:△ABC中 AB=AC
求证: ∠B=∠C
BD=CD=90 °证明:作顶角的平分线AD∠ADB=∠ADC 命题: 等腰三角形的两个底角相等等腰三角形的性质1: 等腰三角形的两个底角相等
(简写成“等边对等角”)在△ABC中
∵ AB=AC ,
∴∠__=∠__
等腰三角形顶角的平分线平分底边并且 垂直于底边。 即: AD 平分 BC,并且 AD ⊥ BC 。 (中线)(高)分析:等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合(三线合一)等腰三角形的性质2:D(1) ∵ AB=AC ,AD是角平分线,
∴ ⊥ , = __.(2) ∵ AB=AC,AD是中线,
∴ ⊥ ,∠_=∠_.(3) ∵ AB=AC,AD 是高,
∴ __ = __,
∠__=∠__.“三线合一”的操作1 填空:在等腰三角形中,
(1)已知顶角为70°,其余两个角分别为_____。
(2)已知底角为70°,其余两个角分别为_____ 。
(3)已知一个角为70°, 其余两个角分别为______
(4)已知一个角为100°,其余两个角分别为_____ 。 55°, 55°70°, 40°55°, 55°或70°, 40°40°, 40°例1 如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。解:∵AB=AC,BC=AD=BD∴∠ABC=∠C=∠BDC
∠A=∠ABD (等边对等角)设∠A=x,则∠BDC=∠A+∠ABD=2X从而∠ABC=∠C=∠BDC=2X于是在△ABC中,有
∠A+∠ABC+∠C=X+2X+2X=1800解得 X=360在△ABC中,∠A=360,∠ABC=∠C=720讨论:猜想一下,等腰三角形底边中点到两腰的距离相等吗?如图所示,你可以将等腰三角形ABC沿对称轴AD折叠,观察DE与DF的关系.
如果DE、DF分别是AB,AC上的中线或∠ADB、∠ADC的平分线,它们还相等吗?由等腰三角形是轴对称图形,利用类似的方法,还可以得到等腰三角形中哪些线段相等。1、研究有关等腰三角形的问题,顶角平分线、底边中线,底边的高是常用的辅助线;2、熟练求解等腰三角形的顶角、底角的度数;
3、掌握等腰三角形三线合一的应用。通过这节课的学习,你有什么发现?怎么发现的?已知:如图,AB=AE, ∠B=∠E,BC=ED.
求证: ∠C=∠D延伸与拓展已知:如图, △ ABC中, ∠ABC=50 o, ∠ACB=80 o,延长
CB至D,使BD=BA,延长BC至E,使CE=CA .连结AD、AE.
求∠D、∠E、∠DAE的度数 .ABCDE
△ADB(AD=BD)
△BDC (BD=BC)大胆猜测等腰三角形除了两腰相等以外,你还能发现什么?等腰三角形的两个底角相等。等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合等腰三角形是轴对称图形.CAB 命题: 等腰三角形的两个底角相等证明:作底边上的高AD ∴Rt△ABD≌Rt△ACD ( ) ∴ ∠B=∠C(全等三角形的对应角相等)已知:△ABC中 AB=AC
求证: ∠B=∠C
AB=AC (已知)AD=AD(公共边)HL在Rt △ ABD和 Rt△ACD中 在△ABD和 △ACD中
AB=AC (已知)
∠1=∠2(辅助线作法)
AD=AD(公共边) ∴△ABD≌△ACD(SAS) ∴ ∠B=∠C(全等三角形的对应角相等)已知:△ABC中 AB=AC
求证: ∠B=∠C
BD=CD=90 °证明:作顶角的平分线AD∠ADB=∠ADC 命题: 等腰三角形的两个底角相等等腰三角形的性质1: 等腰三角形的两个底角相等
(简写成“等边对等角”)在△ABC中
∵ AB=AC ,
∴∠__=∠__
等腰三角形顶角的平分线平分底边并且 垂直于底边。 即: AD 平分 BC,并且 AD ⊥ BC 。 (中线)(高)分析:等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合(三线合一)等腰三角形的性质2:D(1) ∵ AB=AC ,AD是角平分线,
∴ ⊥ , = __.(2) ∵ AB=AC,AD是中线,
∴ ⊥ ,∠_=∠_.(3) ∵ AB=AC,AD 是高,
∴ __ = __,
∠__=∠__.“三线合一”的操作1 填空:在等腰三角形中,
(1)已知顶角为70°,其余两个角分别为_____。
(2)已知底角为70°,其余两个角分别为_____ 。
(3)已知一个角为70°, 其余两个角分别为______
(4)已知一个角为100°,其余两个角分别为_____ 。 55°, 55°70°, 40°55°, 55°或70°, 40°40°, 40°例1 如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。解:∵AB=AC,BC=AD=BD∴∠ABC=∠C=∠BDC
∠A=∠ABD (等边对等角)设∠A=x,则∠BDC=∠A+∠ABD=2X从而∠ABC=∠C=∠BDC=2X于是在△ABC中,有
∠A+∠ABC+∠C=X+2X+2X=1800解得 X=360在△ABC中,∠A=360,∠ABC=∠C=720讨论:猜想一下,等腰三角形底边中点到两腰的距离相等吗?如图所示,你可以将等腰三角形ABC沿对称轴AD折叠,观察DE与DF的关系.
如果DE、DF分别是AB,AC上的中线或∠ADB、∠ADC的平分线,它们还相等吗?由等腰三角形是轴对称图形,利用类似的方法,还可以得到等腰三角形中哪些线段相等。1、研究有关等腰三角形的问题,顶角平分线、底边中线,底边的高是常用的辅助线;2、熟练求解等腰三角形的顶角、底角的度数;
3、掌握等腰三角形三线合一的应用。通过这节课的学习,你有什么发现?怎么发现的?已知:如图,AB=AE, ∠B=∠E,BC=ED.
求证: ∠C=∠D延伸与拓展已知:如图, △ ABC中, ∠ABC=50 o, ∠ACB=80 o,延长
CB至D,使BD=BA,延长BC至E,使CE=CA .连结AD、AE.
求∠D、∠E、∠DAE的度数 .ABCDE
