北师大版数学九年级上册 第四章 图形的相似 专题一 本章易错点例析课件(共28张PPT)
文档属性
| 名称 | 北师大版数学九年级上册 第四章 图形的相似 专题一 本章易错点例析课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 994.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-21 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
1.了解比例的基本性质、线段的比、成比例的线段;通过建筑、艺术上的实例了解黄金分割.
2.通过具体实例认识图形的相似.了解相似多边形和相似比.
3.掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
4.了解相似三角形的判定定理:两角分别相等的两个三角形相似;两边成比例且夹角相等的两个三角形相似;三边成比例的两个三角形相似.*了解相似三角形判定定理的证明.
课程标准
单元复习课
本章知识梳理
5.了解相似三角形的性质定理:相似三角形对应线段的比等于相似比;面积比等于相似比的平方.
6.了解图形的位似,知道利用位似可以将一个图形放大或缩小.
7.会利用图形的相似解决一些简单的实际问题.
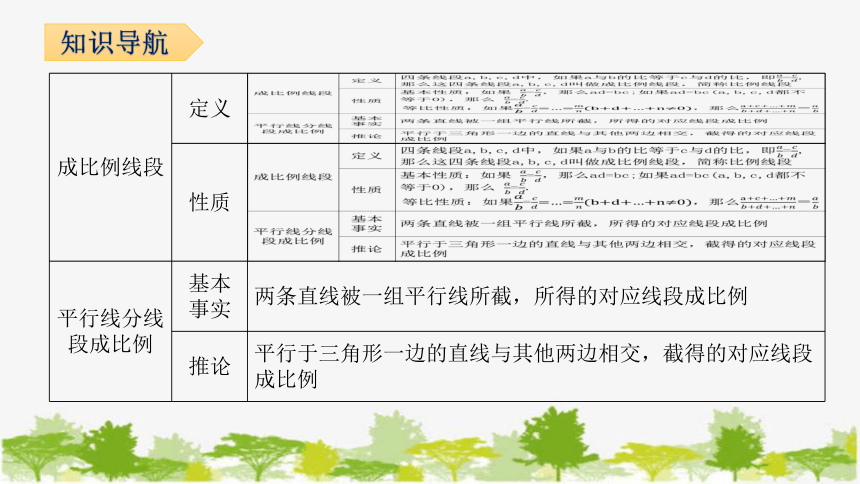
成比例线段 定义
性质
平行线分线段成比例 基本事实 两条直线被一组平行线所截,所得的对应线段成比例
推论 平行于三角形一边的直线与其他两边相交,截得的对应线段成比例
知识导航
续表
相似多边形 定义 各角分别相等、各边成比例的两个多边形叫做相似多边形
性质定理 1.对应角相等、对应边的比等于相似比;
2.周长比等于相似比,面积比等于相似比的平方
相似三角形 定义 三角分别相等、三边对应成比例的两个三角形叫做相似三角形
判定定理 1.两角分别相等的两个三角形相似;
2.两边成比例且夹角相等的两个三角形相似;
3.三边成比例的两个三角形相似
续表
相似三角形 性质定理 1.相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比;
2.相似三角形的周长比等于相似比,面积比等于相似比的平方
利用相似三角形测高 1.利用阳光下的影子测高;
2.利用标杆测高;
3.利用镜子的反射测高
黄金分割 定义及相关概念
续表
图形的位似 位似多边形的定义及相关概念 一般地,如果两个相似多边形任意一组对应顶点P,P′所在直线都经过同一个点O,且有OP′=k·OP(k≠0),那么这样的两个多边形叫做位似多边形, 点O叫做位似中心.实际上,k就是这两个相似多边形的相似比
位似图形的画法 画位似图形的步骤:
(1)确定位似中心;
(2)把位似中心与对应顶点连线(或延长);
(3)根据相似比在所连直线上截取相应线段;
(4)把所截各点用实线连接
平面直角坐标系中的位似变换 在平面直角坐标系中,将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k(k≠0),所对应的图形与原图形位似,位似中心是坐标原点,它们的相似比为|k|
专题一 本章易错点例析
第四章 图形的相似
目录
01
易错典例
02
过关训练
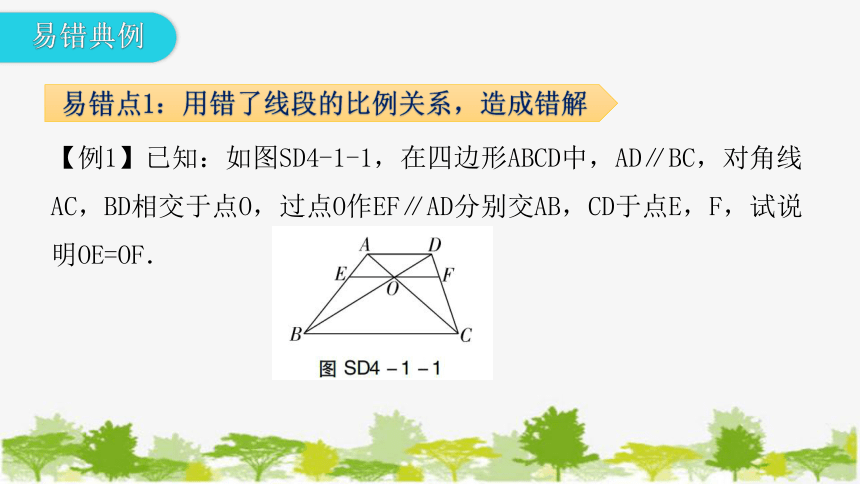
易错点1:用错了线段的比例关系,造成错解
易错典例
【例1】已知:如图SD4-1-1,在四边形ABCD中,AD∥BC,对角线AC,BD相交于点O,过点O作EF∥AD分别交AB,CD于点E,F,试说明OE=OF.
过关训练
2
易错点2:考虑不全面造成漏解
易错典例
【例2】如图SD4-1-3, 已知直角三角形ABC的三边长BC,AC,AB分别为3,4,5,求内接正方形DEFC的边长.
过关训练
2.如图SD4-1-5,△ABC是一块锐角三角形余料,边BC=120 mm,高AD=80 mm,要把它加工成矩形零件PQMN,使一边在BC上,其余两个顶点分别在边AB,AC上.
(1)求证:△APQ∽△ABC;
(2)若这个矩形的边PN∶PQ=1∶2,
则这个矩形的长、宽各是多少?
(1)证明:∵四边形PQMN为矩形,
∴MN∥PQ,即PQ∥BC.
∴△APQ∽△ABC.
(2)解:设矩形的宽为x mm,则长为2x mm.
∵四边形PNMQ为矩形,∴PQ∥BC.
∵AD⊥BC,∴PQ⊥AD.
∵PN∶PQ=1∶2,∴PQ为长,PN为宽.
易错点3:臆造定理造成错解
易错典例
错解分析:上述错误的表现是用两对相似三角形相加,推出待证的两个三角形相似,实际是臆造定理“若两对三角形分别相似,则它们的和也对应相似”.一方面这种臆造意义不明确,两个三角形相加到底是什么相加呢 另一方面即使意义明确,也需要进行严格的证明,这些都没有做到,因而难以让人信服.
过关训练
谢 谢
1.了解比例的基本性质、线段的比、成比例的线段;通过建筑、艺术上的实例了解黄金分割.
2.通过具体实例认识图形的相似.了解相似多边形和相似比.
3.掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
4.了解相似三角形的判定定理:两角分别相等的两个三角形相似;两边成比例且夹角相等的两个三角形相似;三边成比例的两个三角形相似.*了解相似三角形判定定理的证明.
课程标准
单元复习课
本章知识梳理
5.了解相似三角形的性质定理:相似三角形对应线段的比等于相似比;面积比等于相似比的平方.
6.了解图形的位似,知道利用位似可以将一个图形放大或缩小.
7.会利用图形的相似解决一些简单的实际问题.
成比例线段 定义
性质
平行线分线段成比例 基本事实 两条直线被一组平行线所截,所得的对应线段成比例
推论 平行于三角形一边的直线与其他两边相交,截得的对应线段成比例
知识导航
续表
相似多边形 定义 各角分别相等、各边成比例的两个多边形叫做相似多边形
性质定理 1.对应角相等、对应边的比等于相似比;
2.周长比等于相似比,面积比等于相似比的平方
相似三角形 定义 三角分别相等、三边对应成比例的两个三角形叫做相似三角形
判定定理 1.两角分别相等的两个三角形相似;
2.两边成比例且夹角相等的两个三角形相似;
3.三边成比例的两个三角形相似
续表
相似三角形 性质定理 1.相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比;
2.相似三角形的周长比等于相似比,面积比等于相似比的平方
利用相似三角形测高 1.利用阳光下的影子测高;
2.利用标杆测高;
3.利用镜子的反射测高
黄金分割 定义及相关概念
续表
图形的位似 位似多边形的定义及相关概念 一般地,如果两个相似多边形任意一组对应顶点P,P′所在直线都经过同一个点O,且有OP′=k·OP(k≠0),那么这样的两个多边形叫做位似多边形, 点O叫做位似中心.实际上,k就是这两个相似多边形的相似比
位似图形的画法 画位似图形的步骤:
(1)确定位似中心;
(2)把位似中心与对应顶点连线(或延长);
(3)根据相似比在所连直线上截取相应线段;
(4)把所截各点用实线连接
平面直角坐标系中的位似变换 在平面直角坐标系中,将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k(k≠0),所对应的图形与原图形位似,位似中心是坐标原点,它们的相似比为|k|
专题一 本章易错点例析
第四章 图形的相似
目录
01
易错典例
02
过关训练
易错点1:用错了线段的比例关系,造成错解
易错典例
【例1】已知:如图SD4-1-1,在四边形ABCD中,AD∥BC,对角线AC,BD相交于点O,过点O作EF∥AD分别交AB,CD于点E,F,试说明OE=OF.
过关训练
2
易错点2:考虑不全面造成漏解
易错典例
【例2】如图SD4-1-3, 已知直角三角形ABC的三边长BC,AC,AB分别为3,4,5,求内接正方形DEFC的边长.
过关训练
2.如图SD4-1-5,△ABC是一块锐角三角形余料,边BC=120 mm,高AD=80 mm,要把它加工成矩形零件PQMN,使一边在BC上,其余两个顶点分别在边AB,AC上.
(1)求证:△APQ∽△ABC;
(2)若这个矩形的边PN∶PQ=1∶2,
则这个矩形的长、宽各是多少?
(1)证明:∵四边形PQMN为矩形,
∴MN∥PQ,即PQ∥BC.
∴△APQ∽△ABC.
(2)解:设矩形的宽为x mm,则长为2x mm.
∵四边形PNMQ为矩形,∴PQ∥BC.
∵AD⊥BC,∴PQ⊥AD.
∵PN∶PQ=1∶2,∴PQ为长,PN为宽.
易错点3:臆造定理造成错解
易错典例
错解分析:上述错误的表现是用两对相似三角形相加,推出待证的两个三角形相似,实际是臆造定理“若两对三角形分别相似,则它们的和也对应相似”.一方面这种臆造意义不明确,两个三角形相加到底是什么相加呢 另一方面即使意义明确,也需要进行严格的证明,这些都没有做到,因而难以让人信服.
过关训练
谢 谢
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
