人教实验版八上课件14.2.1轴对称变换(一)[上学期]
文档属性
| 名称 | 人教实验版八上课件14.2.1轴对称变换(一)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 587.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-13 00:00:00 | ||
图片预览





文档简介
课件17张PPT。
?
14.2.1 轴对称变换14.2.1 轴对称变换丰南三中八年级数学组课前准备:
按以下步骤操作:
1、自己动手在一张纸上画一个图形。
2、将这张纸折叠、描图。
3、打开纸,看看你得到了什么?
4、改变折痕的位置重复几次。
5、再看看你又得到了什么?
6、和小组的同学交流,看谁画出的图案美观。
动手试一试在一 张半透明的纸的左边画一只左脚印,在把这张纸对折后描图,打开对折的纸。就能得到相应的动脑想一 想左脚印和右脚印有什么关系?
成轴对称对称轴是折痕所在的 直线,即直线l图中的 与 是什么关系?l右脚印
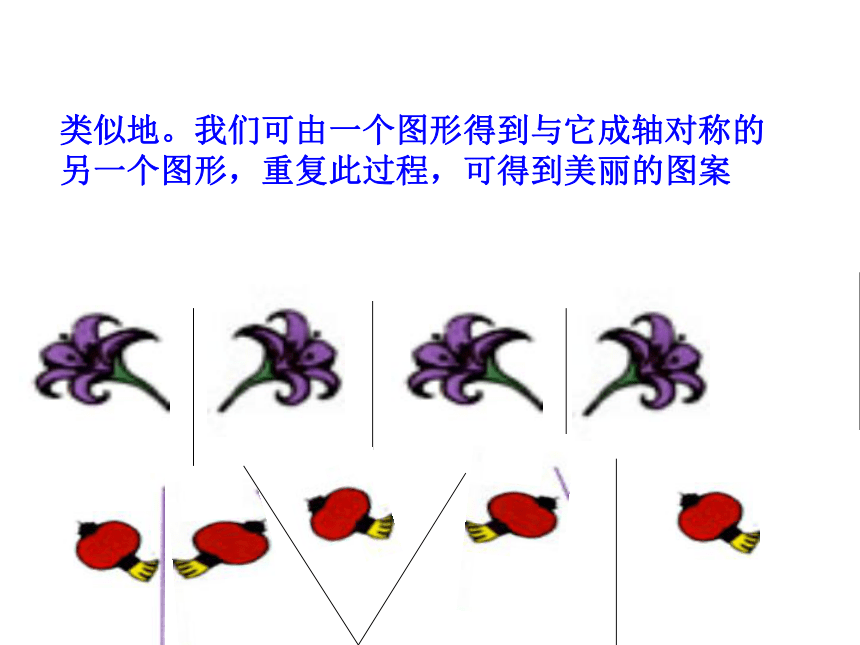
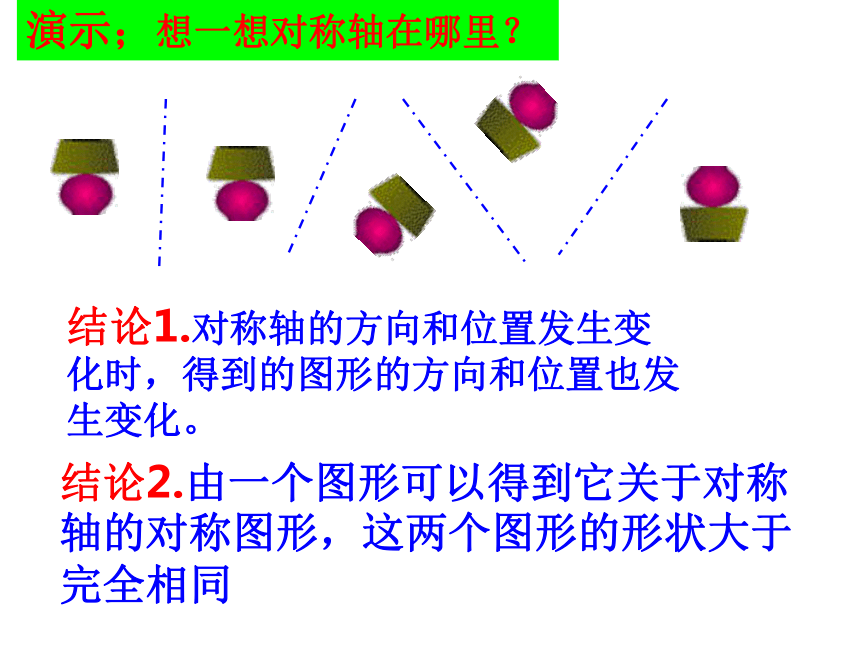
l垂直平分线段PP/类似地。我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案演示;想一想对称轴在哪里?结论1.对称轴的方向和位置发生变化时,得到的图形的方向和位置也发生变化。结论2.由一个图形可以得到它关于对称轴的对称图形,这两个图形的形状大于完全相同由一个平面图形得到它的轴对称图形叫做轴对称变换。归 纳轴对称变换不改变原图形的形状和大小----即所得的图形和原图形全等轴对称变换轴对称变换的性质轴对称图形和轴对称变换的区别:轴对称图形指的是一个图形,这个图形关于一条直线成轴对称;如等腰三角形,正方形等轴对称变换指的是一个图形改变为另一个图形,原图形和另一个图形关于一条直线成轴对称,叙述一个轴对称变换,必须指出原图形和对称轴想一想; 如何作出轴对称变幻的图形?已知对称轴L和一个点A,你能画出点A关于L的对应点A′吗?A·L1、过点A作对称轴L的垂线,垂足为B2、延长AB至A′,使得B A′=ABB3、点A′就是点A关于直线L的对应点探究一1、过点A作对称轴L的垂线A A′,使CA=C A′2.已知对称轴L和一条线段AB,画出线段AB 关于L的对应线段A′B′。ABA′B′L2、过点A作对称轴L的垂线BB′,使DB=DB′3、连接A′B′,线段A′B′就是关于直线
L的对应线段CD探究二探究三3.请同学们拿出一张纸,在上面任意画一个△ABC和一条直线MN,如何作出这个图形关于直线MN的轴对称图形呢?
AA′B′BCC′PQSMN1.已知?ABC和直线m,以直线m为对称轴,作?ABC经轴对称变换后所得的图形作法:1、作AP⊥直线m于P,延长AP至Aˊ,使APˊ=AP,则点Aˊ就是点A关于直线m的对称点,同理点B和点C一样作.2、连结AˊBˊ,BˊCˊ,CˊAˊ?AˊB’C’就是所求的?ABC经轴对称变换后所得的图形试一试AˊBˊCˊ1、分别以虚线为对称轴画出下列各图的另一半,并说明完成后的图案可能代表什么含义。补充完整3. 图中给出了一个图案的一半,其中的虚线是这个图案的对称轴。
(1)你能猜出整个图案的形状吗?
(2)你能画出这些图案的另一半吗? ABCAABBCCDEB′C′C′B′A′C′B′D′E′随 堂 练 习挑战自我 1、请画出⊿ABC关于直线 的对称⊿ A’B’C’.ABC2、画一个正方形,再任意画一条直线,以这条直线为对称轴,画出与正方形成轴对称的图形。先猜一猜,再画一画。ABCD挑战自我课堂小结找关键点作出对称点!然后连结线段.1、画出点A关于 l 的对称点A’:( 3 )点 A’ 就是点A关于 l 的对称点.( 1 )过点A作对称轴 l 的垂线,垂足为B;( 2 )延长A B 至A’,使得BA’= A B.A l 2、画简单平面图形的对称图形:3、利用轴对称设计图案.作业1、某居民小区要在一块长方形空地上建花坛现征集设计方案
要求:(1)设计的图案由若干个长方形和圆组成;
(2)整个长方形场地要成为轴对称图形.
请给出你的设计方案.
?
14.2.1 轴对称变换14.2.1 轴对称变换丰南三中八年级数学组课前准备:
按以下步骤操作:
1、自己动手在一张纸上画一个图形。
2、将这张纸折叠、描图。
3、打开纸,看看你得到了什么?
4、改变折痕的位置重复几次。
5、再看看你又得到了什么?
6、和小组的同学交流,看谁画出的图案美观。
动手试一试在一 张半透明的纸的左边画一只左脚印,在把这张纸对折后描图,打开对折的纸。就能得到相应的动脑想一 想左脚印和右脚印有什么关系?
成轴对称对称轴是折痕所在的 直线,即直线l图中的 与 是什么关系?l右脚印
l垂直平分线段PP/类似地。我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案演示;想一想对称轴在哪里?结论1.对称轴的方向和位置发生变化时,得到的图形的方向和位置也发生变化。结论2.由一个图形可以得到它关于对称轴的对称图形,这两个图形的形状大于完全相同由一个平面图形得到它的轴对称图形叫做轴对称变换。归 纳轴对称变换不改变原图形的形状和大小----即所得的图形和原图形全等轴对称变换轴对称变换的性质轴对称图形和轴对称变换的区别:轴对称图形指的是一个图形,这个图形关于一条直线成轴对称;如等腰三角形,正方形等轴对称变换指的是一个图形改变为另一个图形,原图形和另一个图形关于一条直线成轴对称,叙述一个轴对称变换,必须指出原图形和对称轴想一想; 如何作出轴对称变幻的图形?已知对称轴L和一个点A,你能画出点A关于L的对应点A′吗?A·L1、过点A作对称轴L的垂线,垂足为B2、延长AB至A′,使得B A′=ABB3、点A′就是点A关于直线L的对应点探究一1、过点A作对称轴L的垂线A A′,使CA=C A′2.已知对称轴L和一条线段AB,画出线段AB 关于L的对应线段A′B′。ABA′B′L2、过点A作对称轴L的垂线BB′,使DB=DB′3、连接A′B′,线段A′B′就是关于直线
L的对应线段CD探究二探究三3.请同学们拿出一张纸,在上面任意画一个△ABC和一条直线MN,如何作出这个图形关于直线MN的轴对称图形呢?
AA′B′BCC′PQSMN1.已知?ABC和直线m,以直线m为对称轴,作?ABC经轴对称变换后所得的图形作法:1、作AP⊥直线m于P,延长AP至Aˊ,使APˊ=AP,则点Aˊ就是点A关于直线m的对称点,同理点B和点C一样作.2、连结AˊBˊ,BˊCˊ,CˊAˊ?AˊB’C’就是所求的?ABC经轴对称变换后所得的图形试一试AˊBˊCˊ1、分别以虚线为对称轴画出下列各图的另一半,并说明完成后的图案可能代表什么含义。补充完整3. 图中给出了一个图案的一半,其中的虚线是这个图案的对称轴。
(1)你能猜出整个图案的形状吗?
(2)你能画出这些图案的另一半吗? ABCAABBCCDEB′C′C′B′A′C′B′D′E′随 堂 练 习挑战自我 1、请画出⊿ABC关于直线 的对称⊿ A’B’C’.ABC2、画一个正方形,再任意画一条直线,以这条直线为对称轴,画出与正方形成轴对称的图形。先猜一猜,再画一画。ABCD挑战自我课堂小结找关键点作出对称点!然后连结线段.1、画出点A关于 l 的对称点A’:( 3 )点 A’ 就是点A关于 l 的对称点.( 1 )过点A作对称轴 l 的垂线,垂足为B;( 2 )延长A B 至A’,使得BA’= A B.A l 2、画简单平面图形的对称图形:3、利用轴对称设计图案.作业1、某居民小区要在一块长方形空地上建花坛现征集设计方案
要求:(1)设计的图案由若干个长方形和圆组成;
(2)整个长方形场地要成为轴对称图形.
请给出你的设计方案.
