2022-2023学年高二上学期数学人教A版(2019)第一册3.1.2椭圆的简单几何性质2 课件(共24张PPT)
文档属性
| 名称 | 2022-2023学年高二上学期数学人教A版(2019)第一册3.1.2椭圆的简单几何性质2 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 14.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-21 14:12:06 | ||
图片预览



文档简介
(共24张PPT)
第三章
圆锥曲线的方程
3.1.2椭圆的简单几何性质(2)
要点1椭圆的简单几何性质
焦点的位置
焦点在x轴上
焦点在y轴上
y↑
B
A2
2
图形
A
0
B OF B2
B
A
标准方程
xv
a2 b2
=1(a>b>0)
pbe0)
范围
x≤a,yl≤b
x≤b,lyl≤a
顶点
(±a,0),(0,±b)
(±b,0),(0,±a)
轴长
短轴长=,长轴长=
焦点
(c,0)
(0,±c)
焦距
2c
对称性
对称轴
,对称中心
离心率
e-c
a
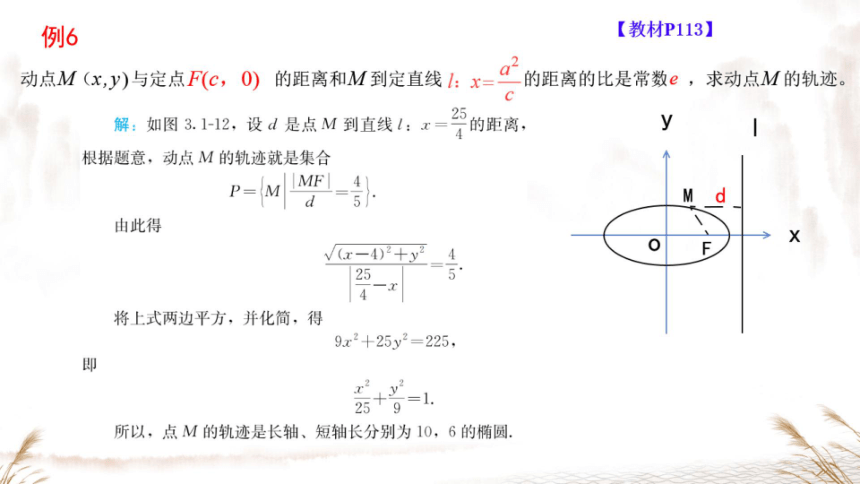
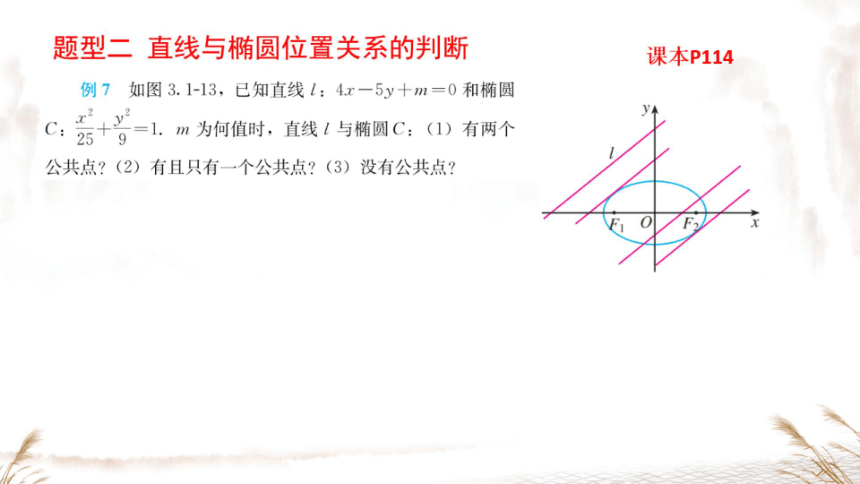
例6
【教材P113】
2
动点M(x,y)与定点F(c,O)
的距离和M到定直线:x=Q的距离的比是常数e,求动点M的轨迹。
C
解:如图3.1-12,设d是点M到直线:x=的距离
y
根据题意,动点M的轨迹就是集合
P-M
MF
4
d
5
M
由此得
X
(x-4)2+y2
2
5
4-x
将上式两边平方,并化简,得
9x2+25y2=225,
即
2
y
25+9=1.
所以,点M的轨迹是长轴、短轴长分别为10,6的椭圆.
点与椭圆、直线与椭圆的位置关系
问题]类比点与圆的位置关系,思考点与椭圆有几种位置关系?
类比直线与圆的位置关系,思考直线与椭圆有几种位置关系?
分别可以怎样判断它们的位置关系?
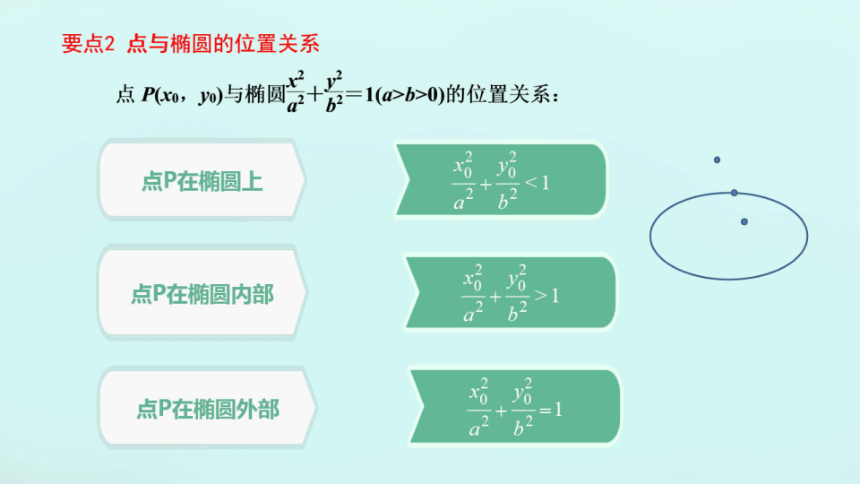
要点2点与椭圆的位置关系
点Ra0与椭圆后+片茶-1cb0的位贸关系:
点P在椭圆上
21
<1
a
2
点P在椭圆内部
0
0
a
点P在椭圆外部
a
62
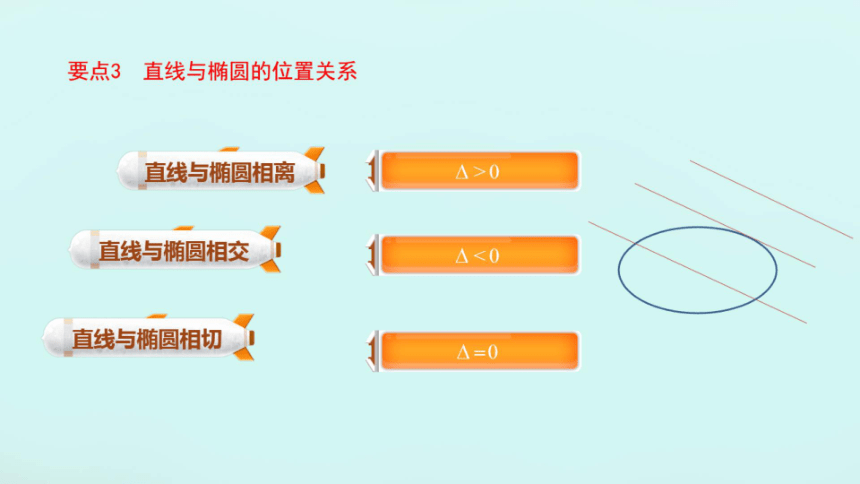
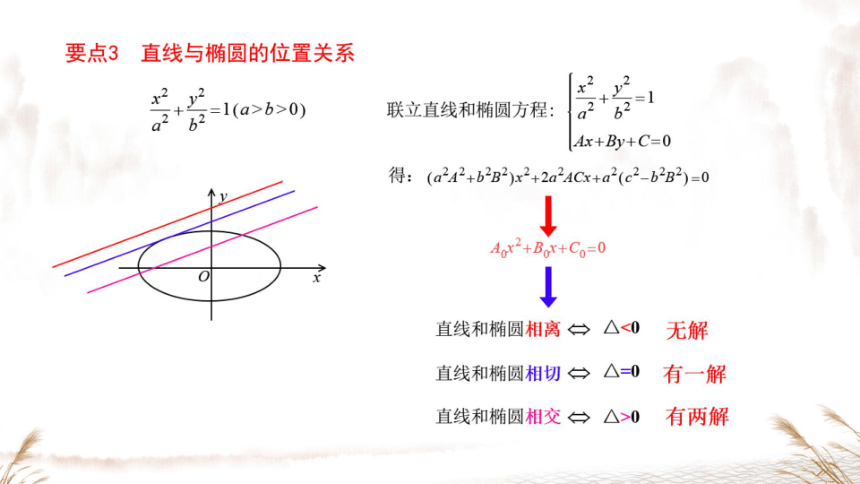
要点3直线与椭圆的位置关系
直线与椭圆相离
△>0
直线与椭圆相交
△<0
直线与椭圆相切
△=0
要点3
直线与椭圆的位置关系
.2
3x3
3
+62=1(a>b>0)
联立直线和椭圆方程:
631
Ax+By+C=0
得:(a2A2+b2B2)x2+2a2ACx+a2(c2-b2B2)=0
Aox2+Box+Co=0
直线和椭圆相离台△<0
无解
直线和椭圆相切一△=0
有一解
直线和椭圆相交台△>0有两解
要点4直线与椭圆相交的弦长公式
1.定义:连接椭圆上两个点的线段称为椭圆的弦.
2.求弦长的方法
()交点法:将直线的方程与椭圆的方程联立,求出两交点的坐标,
然后运用两点间的距离公式来求;
(2)根与系数的关系法:如果直线的斜率为k,被椭圆截得弦AB两端点坐标分别
为(1,y1),(2,y2),则弦长公式为:
AB1=V1+k2·(x1十x2)2-4x2
=1+√0m+z)-42.
第三章
圆锥曲线的方程
3.1.2椭圆的简单几何性质(2)
要点1椭圆的简单几何性质
焦点的位置
焦点在x轴上
焦点在y轴上
y↑
B
A2
2
图形
A
0
B OF B2
B
A
标准方程
xv
a2 b2
=1(a>b>0)
pbe0)
范围
x≤a,yl≤b
x≤b,lyl≤a
顶点
(±a,0),(0,±b)
(±b,0),(0,±a)
轴长
短轴长=,长轴长=
焦点
(c,0)
(0,±c)
焦距
2c
对称性
对称轴
,对称中心
离心率
e-c
a
例6
【教材P113】
2
动点M(x,y)与定点F(c,O)
的距离和M到定直线:x=Q的距离的比是常数e,求动点M的轨迹。
C
解:如图3.1-12,设d是点M到直线:x=的距离
y
根据题意,动点M的轨迹就是集合
P-M
MF
4
d
5
M
由此得
X
(x-4)2+y2
2
5
4-x
将上式两边平方,并化简,得
9x2+25y2=225,
即
2
y
25+9=1.
所以,点M的轨迹是长轴、短轴长分别为10,6的椭圆.
点与椭圆、直线与椭圆的位置关系
问题]类比点与圆的位置关系,思考点与椭圆有几种位置关系?
类比直线与圆的位置关系,思考直线与椭圆有几种位置关系?
分别可以怎样判断它们的位置关系?
要点2点与椭圆的位置关系
点Ra0与椭圆后+片茶-1cb0的位贸关系:
点P在椭圆上
21
<1
a
2
点P在椭圆内部
0
0
a
点P在椭圆外部
a
62
要点3直线与椭圆的位置关系
直线与椭圆相离
△>0
直线与椭圆相交
△<0
直线与椭圆相切
△=0
要点3
直线与椭圆的位置关系
.2
3x3
3
+62=1(a>b>0)
联立直线和椭圆方程:
631
Ax+By+C=0
得:(a2A2+b2B2)x2+2a2ACx+a2(c2-b2B2)=0
Aox2+Box+Co=0
直线和椭圆相离台△<0
无解
直线和椭圆相切一△=0
有一解
直线和椭圆相交台△>0有两解
要点4直线与椭圆相交的弦长公式
1.定义:连接椭圆上两个点的线段称为椭圆的弦.
2.求弦长的方法
()交点法:将直线的方程与椭圆的方程联立,求出两交点的坐标,
然后运用两点间的距离公式来求;
(2)根与系数的关系法:如果直线的斜率为k,被椭圆截得弦AB两端点坐标分别
为(1,y1),(2,y2),则弦长公式为:
AB1=V1+k2·(x1十x2)2-4x2
=1+√0m+z)-42.
