14.2.1轴对称变换(第一课时)[上学期]
文档属性
| 名称 | 14.2.1轴对称变换(第一课时)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-15 00:00:00 | ||
图片预览









文档简介
课件32张PPT。想轻松一下吗?开心时刻A)菊花50我国第五套人民币伍角硬币的背后图案:B)紫荆花C)牡丹花D)荷花E)梅花A)头往后仰从大猩猩的脸部表情以及行为动作
能看出它的情绪。当它非常伤心时是:B)张大嘴巴C)瞪大眼睛D)低头撅嘴60A)斯图加特2006年刘翔在下列哪座城市创造了
12秒88的110米栏的世界记录?B)伯明翰C)巴黎D)洛桑60
?
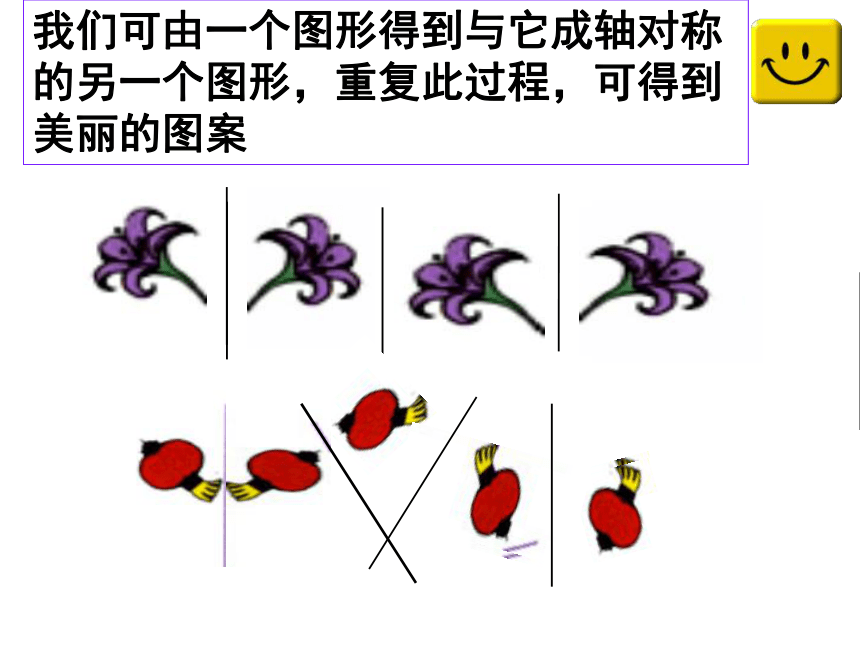
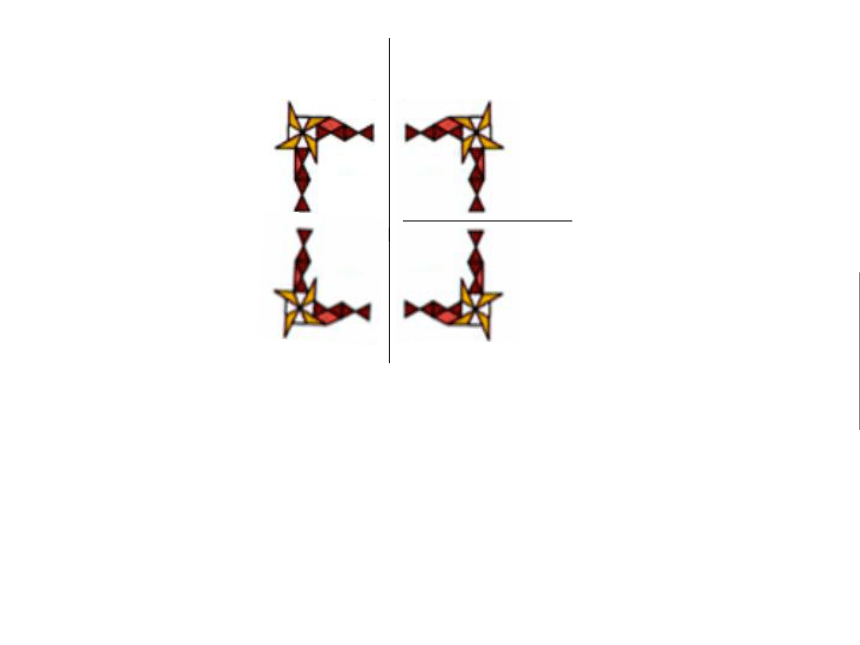
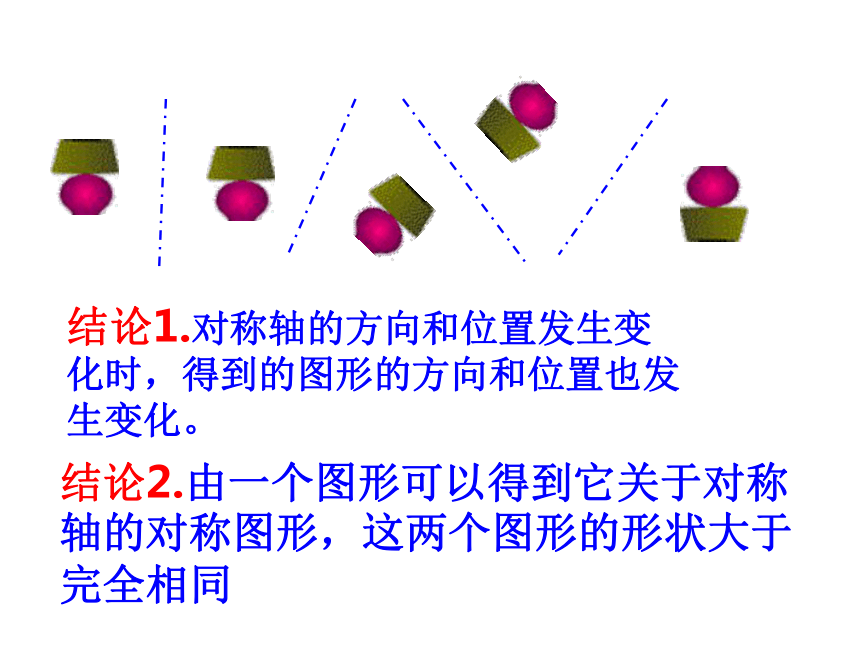
14.2.1 轴对称变换14.2.1 轴对称变换开心走进数学课堂本节课的学习目标:1.理解轴对称变换的性质和定义2.利用轴对称变换的性质作图, 归纳作图方法并练习3.图案欣赏及利用轴对称变换设计简单图案5分钟自学完成1和2两个学习目标请你欣赏轴对称变换我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案结论1.对称轴的方向和位置发生变化时,得到的图形的方向和位置也发生变化。结论2.由一个图形可以得到它关于对称轴的对称图形,这两个图形的形状大于完全相同 由一个平面图形得到它的轴对称图形,这种变换叫轴对称变换.
1、轴对称变换所得的图形与原图形的形状、大小完全一样。2、新图形上的每一点,都是原图形上的某一点关于对称轴的对称点。3、连结任意一对对应点的线段被对称轴垂直平分定义性质你记住了吗一个轴对称图形也可以看作以他的一部分为基础,经轴对称变换扩展而成的。 成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到。 如此漂亮的剪纸是如何剪出来的呢?相信我们学习这节课后也能剪出漂亮的东西?1234实际上:只要将一张纸两次折叠,剪出第1部分的图案,再展开就得到了这美丽的图案。学习目标2:利用轴对称变换的性质作图, 归纳作图方法并练习
课堂检测:作业本(1)36页 1,2,4.试一试 画一个正方形,再任意画一条直线,以这条直线为对称轴,画出与正方形成轴对称的图形。先猜一猜,再画一画。
ABCD技巧 对于一些由直线、射线或线段组成的图形,只要作出图中的一些特殊点的对称点,连结这些对称点,就可以得到原图形的轴对称图形。轴对称变换的性质:
轴对称变换不改变原图形的形状和大小。实际图形和镜中的像有何关系?
欣赏下面这幅风景画,你能找出两个成轴对称的图形吗?看一看1. 周日上午,小明在家复习功课,不知不觉半天过去了,猛抬头看见镜子中后墙上的挂钟已是1点20分,请问实际时间是______.2.小明从平面镜里看到镜子对面电子钟示数的像如图所示,这时的实际时刻应该是_____.请你欣赏几何图案实物图案比一比利用白纸,自己设计一个轴对称图案,看谁做得最漂亮 一次晚会上,主持人出了一道
题“如何把(如图)变成一个真正的等式”,很长时间没有人答出。小兰仅仅拿了一面镜子,就很快解决了这道题。你知道她是怎样做的吗?想一想好,大家来玩一玩推理游戏,
你敢吗? 谜底在此!6 朴素的对称观念在我们的生活中广泛存在:①文学中的对仗也是一种“对称”。王维的诗句“明月松间照,清泉石上流”无非是把第一句中的“明月”变成了第二句中的“清泉”,“松间”变成了“石上”,“照”变成了“流”,词意变了,但是词性和句式结构并没有变.由于工整的文字对仗,使王维诗的自然意境之美得到很好地表现.我国文学中的歌赋尤其是对联,更把“对称”的要求推进到极高的境界. 课外学习阅读讨论 对称与文化哇!只能剪一刀?真神奇! 今天的数学课
你的收获是什么?
还有疑问吗?课堂小结本节课你学到了.2、学会了作简单平面图形的轴对称图形 3、能利用轴对称进行一些图案设计4、体验到了轴对称在现实生活中的广泛应用和丰富的文化价值1、知道了轴对称变换的意义和性质再见
能看出它的情绪。当它非常伤心时是:B)张大嘴巴C)瞪大眼睛D)低头撅嘴60A)斯图加特2006年刘翔在下列哪座城市创造了
12秒88的110米栏的世界记录?B)伯明翰C)巴黎D)洛桑60
?
14.2.1 轴对称变换14.2.1 轴对称变换开心走进数学课堂本节课的学习目标:1.理解轴对称变换的性质和定义2.利用轴对称变换的性质作图, 归纳作图方法并练习3.图案欣赏及利用轴对称变换设计简单图案5分钟自学完成1和2两个学习目标请你欣赏轴对称变换我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案结论1.对称轴的方向和位置发生变化时,得到的图形的方向和位置也发生变化。结论2.由一个图形可以得到它关于对称轴的对称图形,这两个图形的形状大于完全相同 由一个平面图形得到它的轴对称图形,这种变换叫轴对称变换.
1、轴对称变换所得的图形与原图形的形状、大小完全一样。2、新图形上的每一点,都是原图形上的某一点关于对称轴的对称点。3、连结任意一对对应点的线段被对称轴垂直平分定义性质你记住了吗一个轴对称图形也可以看作以他的一部分为基础,经轴对称变换扩展而成的。 成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到。 如此漂亮的剪纸是如何剪出来的呢?相信我们学习这节课后也能剪出漂亮的东西?1234实际上:只要将一张纸两次折叠,剪出第1部分的图案,再展开就得到了这美丽的图案。学习目标2:利用轴对称变换的性质作图, 归纳作图方法并练习
课堂检测:作业本(1)36页 1,2,4.试一试 画一个正方形,再任意画一条直线,以这条直线为对称轴,画出与正方形成轴对称的图形。先猜一猜,再画一画。
ABCD技巧 对于一些由直线、射线或线段组成的图形,只要作出图中的一些特殊点的对称点,连结这些对称点,就可以得到原图形的轴对称图形。轴对称变换的性质:
轴对称变换不改变原图形的形状和大小。实际图形和镜中的像有何关系?
欣赏下面这幅风景画,你能找出两个成轴对称的图形吗?看一看1. 周日上午,小明在家复习功课,不知不觉半天过去了,猛抬头看见镜子中后墙上的挂钟已是1点20分,请问实际时间是______.2.小明从平面镜里看到镜子对面电子钟示数的像如图所示,这时的实际时刻应该是_____.请你欣赏几何图案实物图案比一比利用白纸,自己设计一个轴对称图案,看谁做得最漂亮 一次晚会上,主持人出了一道
题“如何把(如图)变成一个真正的等式”,很长时间没有人答出。小兰仅仅拿了一面镜子,就很快解决了这道题。你知道她是怎样做的吗?想一想好,大家来玩一玩推理游戏,
你敢吗? 谜底在此!6 朴素的对称观念在我们的生活中广泛存在:①文学中的对仗也是一种“对称”。王维的诗句“明月松间照,清泉石上流”无非是把第一句中的“明月”变成了第二句中的“清泉”,“松间”变成了“石上”,“照”变成了“流”,词意变了,但是词性和句式结构并没有变.由于工整的文字对仗,使王维诗的自然意境之美得到很好地表现.我国文学中的歌赋尤其是对联,更把“对称”的要求推进到极高的境界. 课外学习阅读讨论 对称与文化哇!只能剪一刀?真神奇! 今天的数学课
你的收获是什么?
还有疑问吗?课堂小结本节课你学到了.2、学会了作简单平面图形的轴对称图形 3、能利用轴对称进行一些图案设计4、体验到了轴对称在现实生活中的广泛应用和丰富的文化价值1、知道了轴对称变换的意义和性质再见
