3.2.2 双曲线的简单几何性质 第1课时(共23张PPT)
文档属性
| 名称 | 3.2.2 双曲线的简单几何性质 第1课时(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-21 14:29:30 | ||
图片预览







文档简介
(共23张PPT)
双曲线的几何性质(一)
1.掌握双曲线的简单几何性质.
2.理解双曲线的渐近线及离心率的意义.
1.直观想象:通过双曲线几何性质的学习.
2.数学运算:借助双曲线几何性质的应用
我们知道,电能是现代生活不可缺少的能源,目前我国主要靠火力发电,而火力发电主要是在火力发电厂中进行,火力发电厂简称“火电厂”,其形状就像照片中“粗烟囱”.那么这些“粗烟囱”是怎样建成的呢?
冷却通风塔
如果你是设计师你将如何设计?
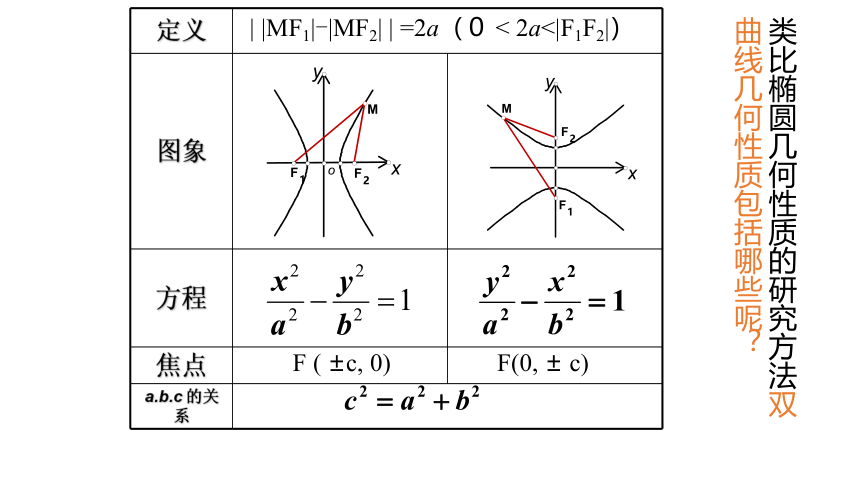
定义 图象
方程
焦点
a.b.c 的关系 | |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
F ( ±c, 0) F(0, ± c)
类比椭圆几何性质的研究方法双曲线几何性质包括哪些呢?
o
Y
X
关于X,Y轴,
原点对称
(±a,0),(0,±b)
(±c,0)
A1A2 ; B1B2
|x| a,|y|≤b
F1
F2
A1
A2
B2
B1
椭圆的图像与性质
|x| b,|y|≤a
关于X,Y轴,
原点对称
(±b,0),(0,±a)
(±c,0)
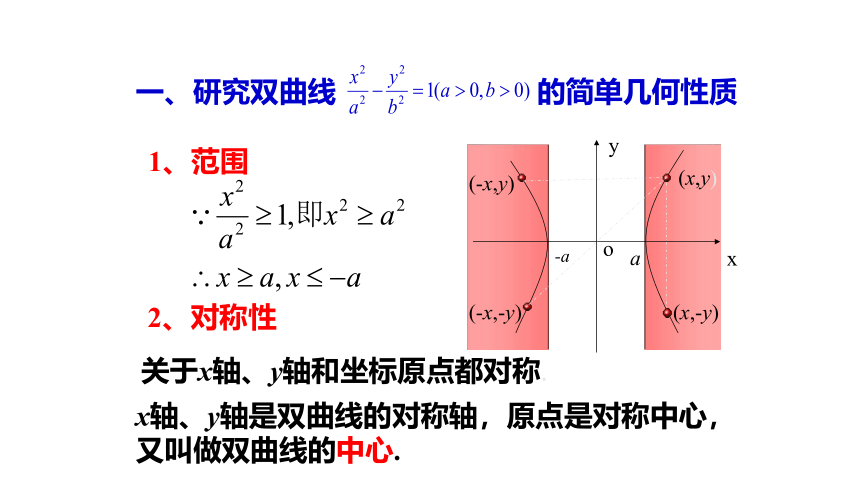
2、对称性
一、研究双曲线 的简单几何性质
1、范围
关于x轴、y轴和坐标原点都对称.
x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心.
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点
x
y
o
-b
b
-a
a
(2)如图,线段A1A2叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段B1B2叫做双曲线的虚轴,它的长为2b, b叫做双曲线的虚半轴长
(4)实轴与虚轴等长的双曲线叫等轴双曲线
(3) B1(0,-b),B2 (0,b)叫做双曲线的虚轴端点
M(x,y)
4、渐近线
N(x,y’)
Q
慢慢靠近
x
y
o
a
b
利用渐近线可以较准确的画出双曲线的草图
5、离心率
离心率.
∵c>a>0
e >1
e是表示双曲线开口大小的一个量,e越大开口越大.
(1)定义:
(2)e的范围:
(3)e的含义:
(4)等轴双曲线的离心率e=
( 5 )
x
y
o
-a
a
b
-b
(1)范围:
(2)对称性:
关于x轴、y轴、原点都对称
(3)顶点:
(0,-a)、(0,a)
(4)渐近线:
(5)离心率:
例1 求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
【解析】把方程9y2-16x2=144化为标准方程
由此可知,实半轴长a=4,虚半轴长b=3;
焦点坐标是(0,-5),(0,5);
变式训练
例2. 求与椭圆
有共同焦点,渐近线方程为
的双曲线方程.
解:
椭圆的焦点在x轴上,且坐标为
双曲线的渐近线方程为
解出
1、若双曲线的渐近线方程为 则双曲线的离心率为 。
2、若双曲线的离心率为2,则两条渐近线斜率为 。
3、求下列双曲线的渐近线方程
(1)4x2-9y2=36,
(2)25x2-4y2=100.
2x±3y=0
5x±2y=0
4、双曲线4x2-9y2=36, 上的一点P到右焦点的距离是5,求P到左焦点的距离.
或
或
关于坐标
轴和
原点
都对
称
性质
双曲线
范围
对称
性
顶点
渐近
线
离心
率
图象
椭 圆 双曲线
方程
a b c关系
图象
椭圆与双曲线的比较
y
X
F1
0
F2
M
X
Y
0
F1
F2
p
1
2
=
+
b
y
a
x
2
2
2
( a> b >0)
1
2
2
2
2
=
-
b
y
a
x
( a> 0 b>0)
2
2
2
=
+
b
a
(a> 0 b>0)
c
2
2
2
=
-
b
a
(a> b>0)
c
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
y
x
O
A2
B2
A1
B1
.
.
F1
F2
y
B2
A1
A2
B1
x
O
.
.
F2
F1
A1(- a,0),A2(a,0)
B1(0,-b),B2(0,b)
F1(-c,0) F2(c,0)
F1(-c,0)
F2(c,0)
关于x轴、y轴、原点对称
A1(- a,0),A2(a,0)
渐近线
无
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
A1(- a,0),A2(a,0)
A1(0,-a),A2(0,a)
关于x轴、y轴、原点对称
渐近线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
x
B1
y
O
.
F2
F1
B2
A1
A2
.
F1(-c,0)
F2(c,0)
F2(0,c)
F1(0,-c)
作业:课本124页练习1,2,3,4
双曲线的几何性质(一)
1.掌握双曲线的简单几何性质.
2.理解双曲线的渐近线及离心率的意义.
1.直观想象:通过双曲线几何性质的学习.
2.数学运算:借助双曲线几何性质的应用
我们知道,电能是现代生活不可缺少的能源,目前我国主要靠火力发电,而火力发电主要是在火力发电厂中进行,火力发电厂简称“火电厂”,其形状就像照片中“粗烟囱”.那么这些“粗烟囱”是怎样建成的呢?
冷却通风塔
如果你是设计师你将如何设计?
定义 图象
方程
焦点
a.b.c 的关系 | |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
F ( ±c, 0) F(0, ± c)
类比椭圆几何性质的研究方法双曲线几何性质包括哪些呢?
o
Y
X
关于X,Y轴,
原点对称
(±a,0),(0,±b)
(±c,0)
A1A2 ; B1B2
|x| a,|y|≤b
F1
F2
A1
A2
B2
B1
椭圆的图像与性质
|x| b,|y|≤a
关于X,Y轴,
原点对称
(±b,0),(0,±a)
(±c,0)
2、对称性
一、研究双曲线 的简单几何性质
1、范围
关于x轴、y轴和坐标原点都对称.
x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心.
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点
x
y
o
-b
b
-a
a
(2)如图,线段A1A2叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段B1B2叫做双曲线的虚轴,它的长为2b, b叫做双曲线的虚半轴长
(4)实轴与虚轴等长的双曲线叫等轴双曲线
(3) B1(0,-b),B2 (0,b)叫做双曲线的虚轴端点
M(x,y)
4、渐近线
N(x,y’)
Q
慢慢靠近
x
y
o
a
b
利用渐近线可以较准确的画出双曲线的草图
5、离心率
离心率.
∵c>a>0
e >1
e是表示双曲线开口大小的一个量,e越大开口越大.
(1)定义:
(2)e的范围:
(3)e的含义:
(4)等轴双曲线的离心率e=
( 5 )
x
y
o
-a
a
b
-b
(1)范围:
(2)对称性:
关于x轴、y轴、原点都对称
(3)顶点:
(0,-a)、(0,a)
(4)渐近线:
(5)离心率:
例1 求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
【解析】把方程9y2-16x2=144化为标准方程
由此可知,实半轴长a=4,虚半轴长b=3;
焦点坐标是(0,-5),(0,5);
变式训练
例2. 求与椭圆
有共同焦点,渐近线方程为
的双曲线方程.
解:
椭圆的焦点在x轴上,且坐标为
双曲线的渐近线方程为
解出
1、若双曲线的渐近线方程为 则双曲线的离心率为 。
2、若双曲线的离心率为2,则两条渐近线斜率为 。
3、求下列双曲线的渐近线方程
(1)4x2-9y2=36,
(2)25x2-4y2=100.
2x±3y=0
5x±2y=0
4、双曲线4x2-9y2=36, 上的一点P到右焦点的距离是5,求P到左焦点的距离.
或
或
关于坐标
轴和
原点
都对
称
性质
双曲线
范围
对称
性
顶点
渐近
线
离心
率
图象
椭 圆 双曲线
方程
a b c关系
图象
椭圆与双曲线的比较
y
X
F1
0
F2
M
X
Y
0
F1
F2
p
1
2
=
+
b
y
a
x
2
2
2
( a> b >0)
1
2
2
2
2
=
-
b
y
a
x
( a> 0 b>0)
2
2
2
=
+
b
a
(a> 0 b>0)
c
2
2
2
=
-
b
a
(a> b>0)
c
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
y
x
O
A2
B2
A1
B1
.
.
F1
F2
y
B2
A1
A2
B1
x
O
.
.
F2
F1
A1(- a,0),A2(a,0)
B1(0,-b),B2(0,b)
F1(-c,0) F2(c,0)
F1(-c,0)
F2(c,0)
关于x轴、y轴、原点对称
A1(- a,0),A2(a,0)
渐近线
无
关于x轴、y轴、原点对称
图形
方程
范围
对称性
顶点
离心率
A1(- a,0),A2(a,0)
A1(0,-a),A2(0,a)
关于x轴、y轴、原点对称
渐近线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
x
B1
y
O
.
F2
F1
B2
A1
A2
.
F1(-c,0)
F2(c,0)
F2(0,c)
F1(0,-c)
作业:课本124页练习1,2,3,4
