14.2轴对称变换[上学期]
文档属性
| 名称 | 14.2轴对称变换[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-24 00:00:00 | ||
图片预览









文档简介
课件45张PPT。
?
?
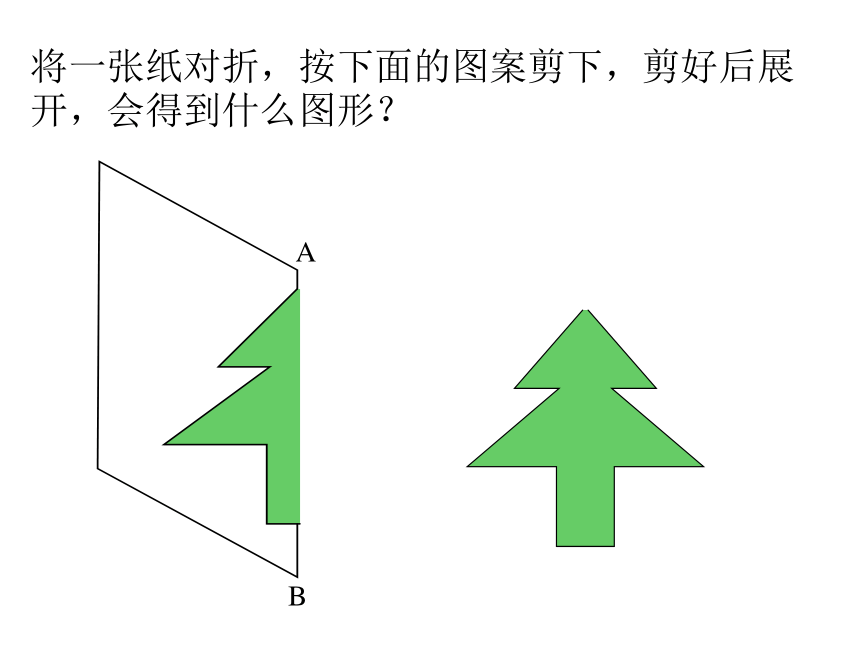
14.2.1 轴对称变换2019-3-16民间剪纸艺术 剪纸是一种民间传统工艺品。早在汉、唐时代,民间妇女即有使用金银箔和彩帛剪成方胜、花鸟贴上鬓角为饰的风尚。后来逐步发展,在节日中,用色纸剪成各种花草、动物或人物故事,贴在窗户上(叫“窗花”)、门楣上(叫“门签”)作为装饰,也有作为礼品装饰或刺绣花样之用的。剪纸的工具,一般只用一把小剪刀,有的职业艺人则用一种特制的刻刀刻制,称为“刻纸”。剪纸艺术 如此漂亮的剪纸是如何剪出来的呢?相信我们学习这节课后也能剪出漂亮的东西?1234实际上:只要将一张纸两次折叠,剪出第1部分的图案,再展开就得到了这美丽的图案。将一张纸对折,按下面的图案剪下,剪好后展开,会得到什么图形?AB(三) 动手做一做 自己动手在一张纸上画一个你最喜欢的图形,将这张纸折叠,描图,再打开纸,看看你得到了什么?改变折痕的位置并重复几次,你又得到了什么?动手试一试动脑想一想【问题】在一 张半透明的纸的左边画一只左脚印,如何由此得到相应的右脚脚印?
1、左脚印和右脚印有什么关系?
2、如何确定对称轴?
3、图中的对应点连线段PP’与对称轴有什么关系?我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案(四)知识要点归纳① 对称轴方向和位置发生变化时,得到的图形的______和
________也会发生变化;
② 由一个平面图形可以得到它关于一条直线 l 对称的图形,
这个图形与原图形的_______、_______完全一样;
③ 新图形上的每一点,都是原图形上的某一点关于直线l
的__________ ;
④连接任意一对对应点的线段被________垂直平分.由一个平面图形得到它的轴对称图形叫做轴对称变换.※ 轴对称变换方向位置形状大小对称点对称轴 像上面那样,由一个平面图形得到它的轴对称图形,叫做轴对称变换。轴对称图形和轴对称变换的区别:轴对称图形指的是一个图形,这个图形关于一条直线成轴对称;如等腰三角形,正方形等轴对称变换指的是一个图形改变为另一个图形,原图形和它的变换后的图形关于一条直线成轴对称,叙述一个轴对称变换,必须指出原图形和对称轴下图是在方格纸上画出的一棵树的一半,以树干为对称轴画出树的另一半。你还记得 “过一点画已知直线的垂线” 吗? 【例1】已知对称轴 l 和一个点A,你能作出点A关于l 的对称点 A′吗?(1) 过点A作对称轴 l 的垂线,垂足为O;(2) 在垂线上截取 O A′= OA .点 A′就是点A关于直线 l 的对应点.Al 作法: 如图,思考 如果有一个图形和一条直线,如何作出与这个图形关于这条直线对称的图形呢?O)A’ 2、 如何画线段AB关于直线 的
对称线段A′B′?找关键点作出其对称点!
然后连结线段.ABABCD 3、如何画△ ABC关于直线 的对称△A′B′C′?还是找关键点作出其对称点!
然后顺次连结线段构成三角形.AB 4、如图给出了一个图案的一半,其中的虚线 是这个图案的对称轴.(1)整个图案是个什么形状?(2)请准确地画出它的另一半.还是找关键点作出其对称点!①几何图形都可以看作由点组成,只要分别作出这些点关于对称轴的对应点,再连接这些对应点,就可以得到原图形的轴对称图形。②对于一些由直线、线段或射线组成的图形只要作出图形中的一些特殊点的对称点,连接这些对称点,就可以得到原图形的轴对称图形。归 纳 已知对称轴L和四边形ABCD经轴对称变换后所得的图形注:对称轴上的点的对应点是它本身 1 、分别以虚线为对称轴画出下列各图的另一半,并说明完成后的图案可能代表什么含义。 2、画一个正方形,再任意画一条直线,以这条直线为对称轴,画出与正方形成轴对称的图形。先猜一猜,再画一画。猜字游戏:通过怎样轴对称变换,将图中的甲图案变成乙图案?甲乙AB议一议甲乙AB通过怎样轴对称变换,将图中的甲图案变成乙图案?议一议甲乙AB通过怎样轴对称变换,将图中的甲图案变成乙图案?议一议路径的合理选择 到达目的地可能有很多条路,能找出一条合理的路径,并解释为什么合理是人的智慧的展现。老师寄语例1 如图:设L1,L2是平行且镜面相对的两面镜子,把一个小球A放在L1,L2之间,小球在镜L1中的像为A1,A在镜L2中的像为A2,当L1,L2间的距离为18厘米。
(1)试求A1与A2间的距离;
(2)若小球在L1,L2间运动, A1 与A2 间的距离改变吗?AL1L2A1A2BC解:如图,∵ A 与 A1关于L1对称, A 与 A2关于L2对称
∴ A1 B=AB, A2 C=AC
∴A1A2=2BC=36厘米
答:A1与A2间的距离为36厘米。
例1 如图:设L1,L2是平行且镜面相对的两面镜子,把一个小球A放在L1,L2之间,小球在镜L1中的像为A1,A在镜L2中的像为A2,当L1,L2间的距离为18厘米。
(1)试求A1与A2间的距离;
(2)若小球在L1,L2间运动,
A1与A2 间的距离改变吗?AL1L2A1A2BC解: (1)如图,∵ A 与 A1关于L1对称, A 与 A2关于L2对称
∴ A1 B=AB, A2 C=AC
∴A1A2=2BC=36厘米
答:A1与A2间的距离为36厘米。
(2)答:不论A 在L1,L2间的哪个位置,A1与A2 间的距离都不会改变吗。
例2 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,(1)当汽车行驶到什么位置时距村庄M最近?行驶到什么位置时距村庄N最近?答:如图 ,当汽车行驶到P1时,距村庄M最近,
当汽车行驶到P2时,距村庄N最近。
ABMNP1P2根据:直线外一点与直线上各点连结的所有线段中,
垂线段最短。例2 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,(2)当汽车行驶到什么位置时,与村庄M、N的距离相等?
答:如图 ,当汽车行驶到P3时,与村庄M、N的距离相等。
ABMNP3根据:线段的垂直平分线上的点到这条线段两个端点的距离相等。
例2 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,(3)当汽车行驶到什么位置时,到村庄M、N的距离之和最短?
答:如图 ,当汽车行驶到P4时,到村庄M、N的距离之和最短。
ABMNP4根据:两点之间线段最短。又问:若村庄M,N在公路AB的同侧,则又如何解决此题?N1P5答:若村庄M,N在公路AB的同侧时,当汽车行驶到P5时,到村庄M、N的距离之和最短。
, 如图,一只蚂蚁,在正方体箱子的一个顶点A,它发现另一个顶点B处有它感兴趣的食物,这只蚂蚁想尽快得到食物,哪条路径最短?试在图中将路线画出来。.一只蚂蚁
在点A处AB在点B
发现食物. 如图,一只蚂蚁,在正方体箱子的一个顶点A,它发现相距它很远的另一个顶点B处有它感兴趣的食物,这只蚂蚁想尽快得到食物,哪条路径最短?试在图中将路线画出来。.一只蚂蚁
在点A处AB在点B
发现食物.AB1B2...做一做1.A、B两村庄要建立一个加油站,要求到A、B两
村距离相等,且到公路a、b的距离也相等,请你帮
忙确定加油站的位置P.abAB12P∟练一练1.如图,点P、Q是锐角∠AOB内的两点,求作两点M、N
使M在OA上,N在OB上, 且使PM+MN+NQ最小.解答:作P点关于OA的像P1, Q点关于OB的像Q1, 则PM+MN+NQ=P1M+MN+NQ1因为由光走最短路径可知, 当PM+MN+NQ可成
由P点发出的光经M点反射传播到N点,再经N点反
射后传播到Q点所走的总路程时, PM+MN+NQ最小,即P1M+MN+NQ1最小.所以P1、M、N、Q1四点共线.故连P1Q1, 分别与OA、OB的交点即是求作的M、N .ABPQP1Q1MNO课外延伸题 动脑筋1.如图,EFGH为长方形的台球台面,有黑、白两球分别位于A、B两点的位置上,怎样撞击黑球A,使黑球先碰撞台边FG,反弹后再撞击台边GH,再反弹后击中白球B?作出FG、GH上的撞击点的位置和黑球的运行路线.FEHGABFEHGAB∟CA1DB1MN∟竞赛台思想方法探究天地1.如图,点A、B的坐标分别为(-1,1)、(3,2),P为 x 轴上一点,且P到A、B的之和最小,则P的坐标为_________
2.试求函数(第18届江苏省竞赛题)(2004年四川省竞赛题)3.如图,在矩形台球桌ABCD上,放有P和Q两个求,恰有
∠PAB和∠QAD相等,如果打击球P使它撞在AB的M点反
弹后撞到球Q,其路线记为 P→M→Q; 如果打击球Q使它撞
在AD的N点反弹后撞到球P,其路线记为Q→N→P。证明:
P→M→Q与Q→N→P的路线的长相等。ABCDPQ(上海市第20届竞赛题)4.如图,已知正方形ABCD的边长为8, M在DC,且DM=2,N是AC上的一动点,则DN+MN的最小值是_____________
试一试 D、M为AC同侧两定点,从对称性考虑确定N点的位置 。 (2004年黑龙江中考题)ABCD5.如图,在矩形ABCD中,
AB = 8,BC = 4,将矩形沿AC折叠,
则重叠的部分△AFC的面积为( )
A. 12 B. 10 C. 8 D. 6ADBCD1F(2004年河北省中考题)MN10C7.如图在三角形 ABC中,AB=3 , AC = 4, BC = 5, 现将它折叠, 使点B与点C重合, 则折痕的长是__________ABC(2004年我爱数学初中夏令营竞赛题)7.如图在三角形 ABC中,AB=3 , AC = 4, BC = 5, 现将它折叠, 使点B与点C重合, 则折痕的长是__________8.如图,在菱形ABCD 中,AB = 4a , E在BC上, BE = 2a ,∠BAD = ,P点在BD上,则 PE + PC 的最小值为( )
A.6a B.5a C.4a D. ABCDPE(2004年武汉市选拔赛试题)小结:1、由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全一样。2、经轴对称变换后的图形与原图形上的对应点连线被对称轴垂直平分。3、画一个图形经轴对称变换后的图形,关键是找到图形上的一些关键点,作出这些点的对称点。
?
?
14.2.1 轴对称变换2019-3-16民间剪纸艺术 剪纸是一种民间传统工艺品。早在汉、唐时代,民间妇女即有使用金银箔和彩帛剪成方胜、花鸟贴上鬓角为饰的风尚。后来逐步发展,在节日中,用色纸剪成各种花草、动物或人物故事,贴在窗户上(叫“窗花”)、门楣上(叫“门签”)作为装饰,也有作为礼品装饰或刺绣花样之用的。剪纸的工具,一般只用一把小剪刀,有的职业艺人则用一种特制的刻刀刻制,称为“刻纸”。剪纸艺术 如此漂亮的剪纸是如何剪出来的呢?相信我们学习这节课后也能剪出漂亮的东西?1234实际上:只要将一张纸两次折叠,剪出第1部分的图案,再展开就得到了这美丽的图案。将一张纸对折,按下面的图案剪下,剪好后展开,会得到什么图形?AB(三) 动手做一做 自己动手在一张纸上画一个你最喜欢的图形,将这张纸折叠,描图,再打开纸,看看你得到了什么?改变折痕的位置并重复几次,你又得到了什么?动手试一试动脑想一想【问题】在一 张半透明的纸的左边画一只左脚印,如何由此得到相应的右脚脚印?
1、左脚印和右脚印有什么关系?
2、如何确定对称轴?
3、图中的对应点连线段PP’与对称轴有什么关系?我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案(四)知识要点归纳① 对称轴方向和位置发生变化时,得到的图形的______和
________也会发生变化;
② 由一个平面图形可以得到它关于一条直线 l 对称的图形,
这个图形与原图形的_______、_______完全一样;
③ 新图形上的每一点,都是原图形上的某一点关于直线l
的__________ ;
④连接任意一对对应点的线段被________垂直平分.由一个平面图形得到它的轴对称图形叫做轴对称变换.※ 轴对称变换方向位置形状大小对称点对称轴 像上面那样,由一个平面图形得到它的轴对称图形,叫做轴对称变换。轴对称图形和轴对称变换的区别:轴对称图形指的是一个图形,这个图形关于一条直线成轴对称;如等腰三角形,正方形等轴对称变换指的是一个图形改变为另一个图形,原图形和它的变换后的图形关于一条直线成轴对称,叙述一个轴对称变换,必须指出原图形和对称轴下图是在方格纸上画出的一棵树的一半,以树干为对称轴画出树的另一半。你还记得 “过一点画已知直线的垂线” 吗? 【例1】已知对称轴 l 和一个点A,你能作出点A关于l 的对称点 A′吗?(1) 过点A作对称轴 l 的垂线,垂足为O;(2) 在垂线上截取 O A′= OA .点 A′就是点A关于直线 l 的对应点.Al 作法: 如图,思考 如果有一个图形和一条直线,如何作出与这个图形关于这条直线对称的图形呢?O)A’ 2、 如何画线段AB关于直线 的
对称线段A′B′?找关键点作出其对称点!
然后连结线段.ABABCD 3、如何画△ ABC关于直线 的对称△A′B′C′?还是找关键点作出其对称点!
然后顺次连结线段构成三角形.AB 4、如图给出了一个图案的一半,其中的虚线 是这个图案的对称轴.(1)整个图案是个什么形状?(2)请准确地画出它的另一半.还是找关键点作出其对称点!①几何图形都可以看作由点组成,只要分别作出这些点关于对称轴的对应点,再连接这些对应点,就可以得到原图形的轴对称图形。②对于一些由直线、线段或射线组成的图形只要作出图形中的一些特殊点的对称点,连接这些对称点,就可以得到原图形的轴对称图形。归 纳 已知对称轴L和四边形ABCD经轴对称变换后所得的图形注:对称轴上的点的对应点是它本身 1 、分别以虚线为对称轴画出下列各图的另一半,并说明完成后的图案可能代表什么含义。 2、画一个正方形,再任意画一条直线,以这条直线为对称轴,画出与正方形成轴对称的图形。先猜一猜,再画一画。猜字游戏:通过怎样轴对称变换,将图中的甲图案变成乙图案?甲乙AB议一议甲乙AB通过怎样轴对称变换,将图中的甲图案变成乙图案?议一议甲乙AB通过怎样轴对称变换,将图中的甲图案变成乙图案?议一议路径的合理选择 到达目的地可能有很多条路,能找出一条合理的路径,并解释为什么合理是人的智慧的展现。老师寄语例1 如图:设L1,L2是平行且镜面相对的两面镜子,把一个小球A放在L1,L2之间,小球在镜L1中的像为A1,A在镜L2中的像为A2,当L1,L2间的距离为18厘米。
(1)试求A1与A2间的距离;
(2)若小球在L1,L2间运动, A1 与A2 间的距离改变吗?AL1L2A1A2BC解:如图,∵ A 与 A1关于L1对称, A 与 A2关于L2对称
∴ A1 B=AB, A2 C=AC
∴A1A2=2BC=36厘米
答:A1与A2间的距离为36厘米。
例1 如图:设L1,L2是平行且镜面相对的两面镜子,把一个小球A放在L1,L2之间,小球在镜L1中的像为A1,A在镜L2中的像为A2,当L1,L2间的距离为18厘米。
(1)试求A1与A2间的距离;
(2)若小球在L1,L2间运动,
A1与A2 间的距离改变吗?AL1L2A1A2BC解: (1)如图,∵ A 与 A1关于L1对称, A 与 A2关于L2对称
∴ A1 B=AB, A2 C=AC
∴A1A2=2BC=36厘米
答:A1与A2间的距离为36厘米。
(2)答:不论A 在L1,L2间的哪个位置,A1与A2 间的距离都不会改变吗。
例2 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,(1)当汽车行驶到什么位置时距村庄M最近?行驶到什么位置时距村庄N最近?答:如图 ,当汽车行驶到P1时,距村庄M最近,
当汽车行驶到P2时,距村庄N最近。
ABMNP1P2根据:直线外一点与直线上各点连结的所有线段中,
垂线段最短。例2 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,(2)当汽车行驶到什么位置时,与村庄M、N的距离相等?
答:如图 ,当汽车行驶到P3时,与村庄M、N的距离相等。
ABMNP3根据:线段的垂直平分线上的点到这条线段两个端点的距离相等。
例2 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,(3)当汽车行驶到什么位置时,到村庄M、N的距离之和最短?
答:如图 ,当汽车行驶到P4时,到村庄M、N的距离之和最短。
ABMNP4根据:两点之间线段最短。又问:若村庄M,N在公路AB的同侧,则又如何解决此题?N1P5答:若村庄M,N在公路AB的同侧时,当汽车行驶到P5时,到村庄M、N的距离之和最短。
, 如图,一只蚂蚁,在正方体箱子的一个顶点A,它发现另一个顶点B处有它感兴趣的食物,这只蚂蚁想尽快得到食物,哪条路径最短?试在图中将路线画出来。.一只蚂蚁
在点A处AB在点B
发现食物. 如图,一只蚂蚁,在正方体箱子的一个顶点A,它发现相距它很远的另一个顶点B处有它感兴趣的食物,这只蚂蚁想尽快得到食物,哪条路径最短?试在图中将路线画出来。.一只蚂蚁
在点A处AB在点B
发现食物.AB1B2...做一做1.A、B两村庄要建立一个加油站,要求到A、B两
村距离相等,且到公路a、b的距离也相等,请你帮
忙确定加油站的位置P.abAB12P∟练一练1.如图,点P、Q是锐角∠AOB内的两点,求作两点M、N
使M在OA上,N在OB上, 且使PM+MN+NQ最小.解答:作P点关于OA的像P1, Q点关于OB的像Q1, 则PM+MN+NQ=P1M+MN+NQ1因为由光走最短路径可知, 当PM+MN+NQ可成
由P点发出的光经M点反射传播到N点,再经N点反
射后传播到Q点所走的总路程时, PM+MN+NQ最小,即P1M+MN+NQ1最小.所以P1、M、N、Q1四点共线.故连P1Q1, 分别与OA、OB的交点即是求作的M、N .ABPQP1Q1MNO课外延伸题 动脑筋1.如图,EFGH为长方形的台球台面,有黑、白两球分别位于A、B两点的位置上,怎样撞击黑球A,使黑球先碰撞台边FG,反弹后再撞击台边GH,再反弹后击中白球B?作出FG、GH上的撞击点的位置和黑球的运行路线.FEHGABFEHGAB∟CA1DB1MN∟竞赛台思想方法探究天地1.如图,点A、B的坐标分别为(-1,1)、(3,2),P为 x 轴上一点,且P到A、B的之和最小,则P的坐标为_________
2.试求函数(第18届江苏省竞赛题)(2004年四川省竞赛题)3.如图,在矩形台球桌ABCD上,放有P和Q两个求,恰有
∠PAB和∠QAD相等,如果打击球P使它撞在AB的M点反
弹后撞到球Q,其路线记为 P→M→Q; 如果打击球Q使它撞
在AD的N点反弹后撞到球P,其路线记为Q→N→P。证明:
P→M→Q与Q→N→P的路线的长相等。ABCDPQ(上海市第20届竞赛题)4.如图,已知正方形ABCD的边长为8, M在DC,且DM=2,N是AC上的一动点,则DN+MN的最小值是_____________
试一试 D、M为AC同侧两定点,从对称性考虑确定N点的位置 。 (2004年黑龙江中考题)ABCD5.如图,在矩形ABCD中,
AB = 8,BC = 4,将矩形沿AC折叠,
则重叠的部分△AFC的面积为( )
A. 12 B. 10 C. 8 D. 6ADBCD1F(2004年河北省中考题)MN10C7.如图在三角形 ABC中,AB=3 , AC = 4, BC = 5, 现将它折叠, 使点B与点C重合, 则折痕的长是__________ABC(2004年我爱数学初中夏令营竞赛题)7.如图在三角形 ABC中,AB=3 , AC = 4, BC = 5, 现将它折叠, 使点B与点C重合, 则折痕的长是__________8.如图,在菱形ABCD 中,AB = 4a , E在BC上, BE = 2a ,∠BAD = ,P点在BD上,则 PE + PC 的最小值为( )
A.6a B.5a C.4a D. ABCDPE(2004年武汉市选拔赛试题)小结:1、由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全一样。2、经轴对称变换后的图形与原图形上的对应点连线被对称轴垂直平分。3、画一个图形经轴对称变换后的图形,关键是找到图形上的一些关键点,作出这些点的对称点。
