轴对称变换[上学期]
图片预览


文档简介
课件14张PPT。14.2 轴对称变换复习引入讲授新课课堂练习应用新知小结上一页下一页退出复习引入2、 如果把一个等腰三角形沿着它的底边上的高对折,
将会有什么结果?请思考下列问题:3、 观察下面两个图形,你能发现它们有什么特点吗?上一页下一页1、 什么叫线段垂直平分线,它的性质定理和逆定理是
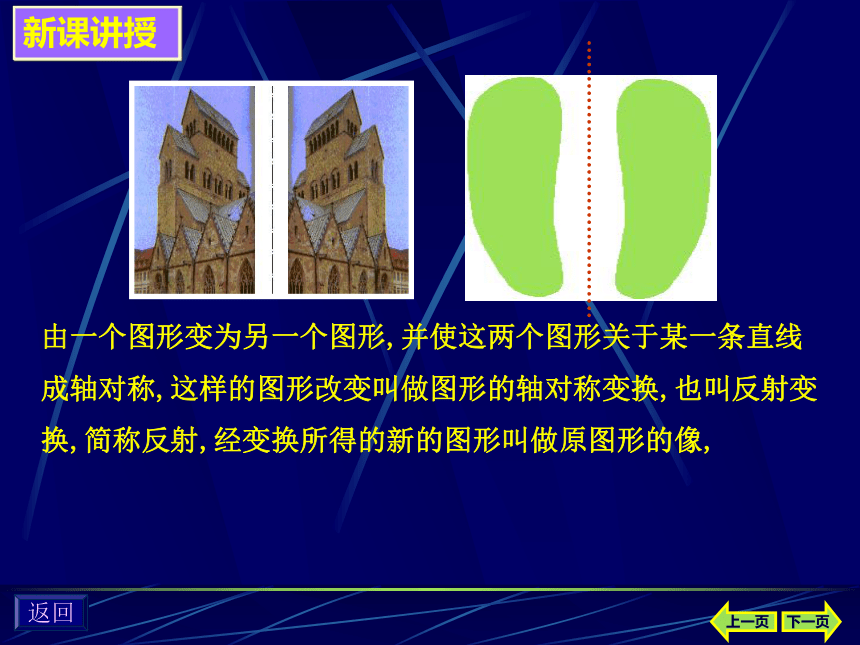
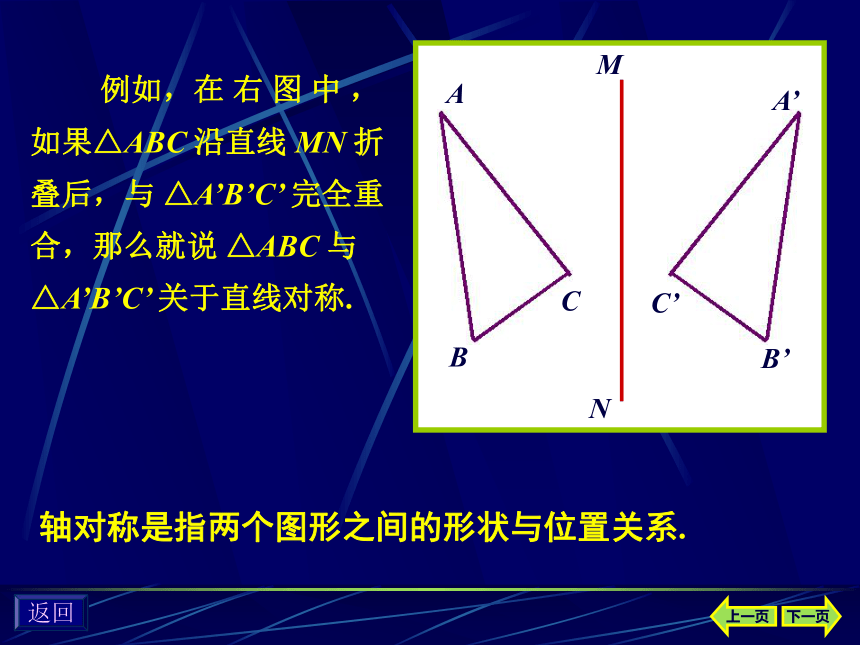
什么?返回新课讲授由一个图形变为另一个图形,并使这两个图形关于某一条直线成轴对称,这样的图形改变叫做图形的轴对称变换,也叫反射变换,简称反射,经变换所得的新的图形叫做原图形的像,上一页下一页返回 例如,在 右 图 中 ,如果△ABC 沿直线 MN 折叠后,与 △A’B’C’ 完全重合,那么就说 △ABC 与 △A’B’C’ 关于直线对称.轴对称是指两个图形之间的形状与位置关系.上一页下一页返回上一页 △ABC 与 △A’B’C’关于直线对称. 则
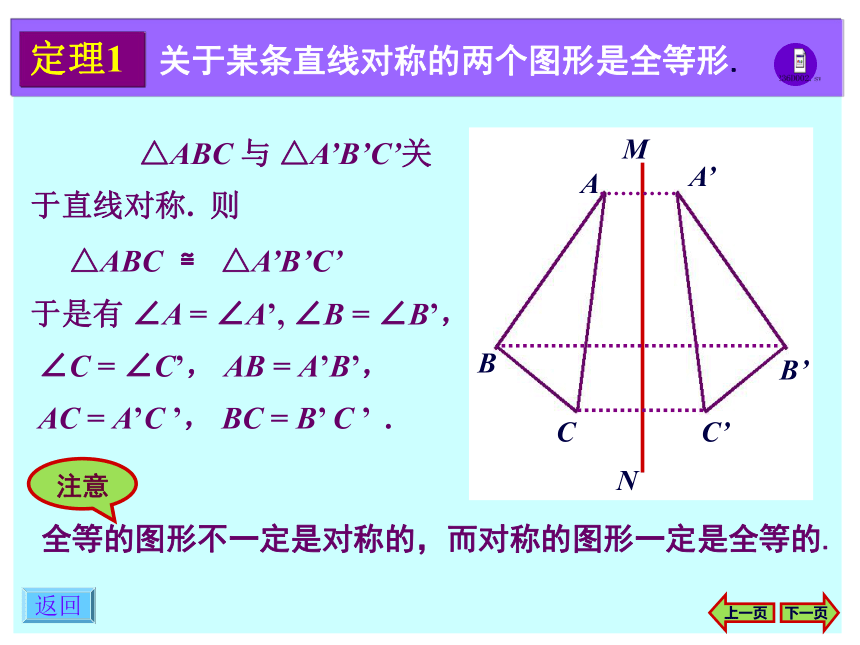
△ABC ≌ △A’B’C’
于是有 ∠A = ∠A’, ∠B = ∠B’,
∠C = ∠C’, AB = A’B’,
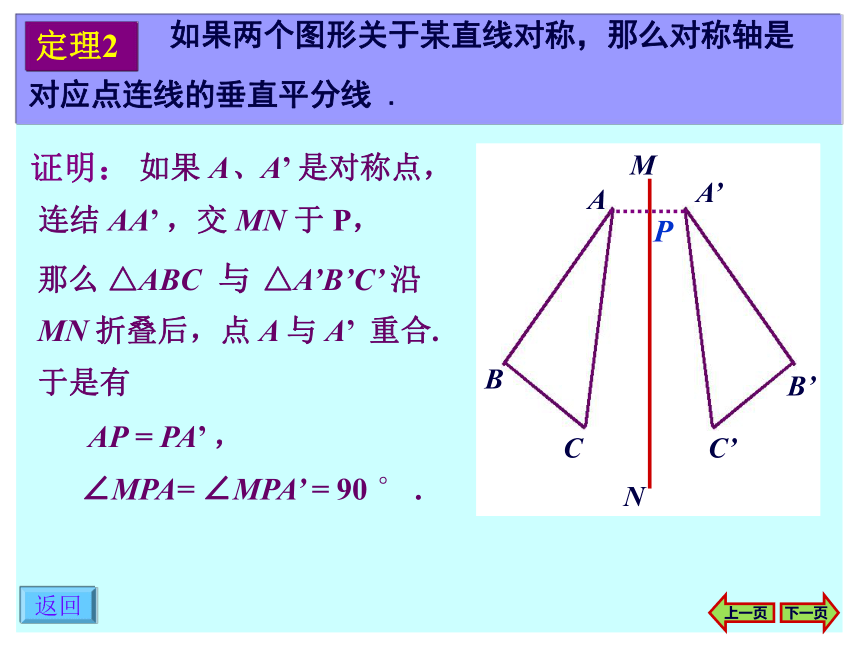
AC = A’C ’, BC = B’ C ’ .下一页全等的图形不一定是对称的,而对称的图形一定是全等的.注意返回上一页 如果 A、A’ 是对称点,
连结 AA’ ,交 MN 于 P,下一页证明: AP = PA’ ,
∠MPA= ∠MPA’ = 90 ° .那么 △ABC 与 △A’B’C’ 沿 MN 折叠后,点 A 与 A’ 重合.
于是有P返回上一页下一页逆定理 如果两个图形的对应点连线被同一条直线垂
直平分,那么这两个图形关于这条直线对称.这个逆定理可以判定两个图形是否关于某直线对称,
它是作对称图形的主要依据. 返回 已知:如图,直线 l 及直线外一点 P.
求作:点 P’ ,使它与点 P 关于直线 l 对称.例 1 作法: POQP’1. 过点 P 作 PQ ⊥l ,交 l 与点 O . 2. 在直线 PQ 上,取 OP’ = OP . 点 P’ 为所作的点 .l上一页下一页返回巩固练习1.已知:如图,点 P 在直线 l 上,则
点 P 关于直线 l 的对称点在什么地方?(第1题)2.已知:如图,两点 A、B. 求作:
直线 l ,使点 A、B 关于直线 l 对称.AB(第2题)返回上一页下一页巩固练习3.已知: △ABC ≌△A’B’C’ , 那么 △ABC 与△A’B’C’
一定关于某直线对称吗?如果 △ABC 与△A’B’C’ 关于某直线对称,那么它们全等吗?为什么?4. 已知:如图, MN 垂直平分线段
AB 、CD,垂足分别是 E、F .
求证: AB = CD,∠ ACD= ∠ BDC .(提示:可用对称关系来证.)上一页下一页返回上一页下一页 水泵站修在什么地方?如图所示,水泵站修在 C 点可使所用的水管最短. 如图,要在河边修建一个水泵站,分别向张村、李庄送水,修在河边什么地方,可使所用的水管最短?张村李庄A’C返回应用新知小 结1、 要掌握轴对称变换的概念.2、 要掌握关于一条直线对称的两个图形的性质和判定,并会画出一个点的对称点.3、 除定义外,有什么方法可以判定两个图形成轴对称?上一页下一页返回作业P 135第1、2、4题 谢谢!
将会有什么结果?请思考下列问题:3、 观察下面两个图形,你能发现它们有什么特点吗?上一页下一页1、 什么叫线段垂直平分线,它的性质定理和逆定理是
什么?返回新课讲授由一个图形变为另一个图形,并使这两个图形关于某一条直线成轴对称,这样的图形改变叫做图形的轴对称变换,也叫反射变换,简称反射,经变换所得的新的图形叫做原图形的像,上一页下一页返回 例如,在 右 图 中 ,如果△ABC 沿直线 MN 折叠后,与 △A’B’C’ 完全重合,那么就说 △ABC 与 △A’B’C’ 关于直线对称.轴对称是指两个图形之间的形状与位置关系.上一页下一页返回上一页 △ABC 与 △A’B’C’关于直线对称. 则
△ABC ≌ △A’B’C’
于是有 ∠A = ∠A’, ∠B = ∠B’,
∠C = ∠C’, AB = A’B’,
AC = A’C ’, BC = B’ C ’ .下一页全等的图形不一定是对称的,而对称的图形一定是全等的.注意返回上一页 如果 A、A’ 是对称点,
连结 AA’ ,交 MN 于 P,下一页证明: AP = PA’ ,
∠MPA= ∠MPA’ = 90 ° .那么 △ABC 与 △A’B’C’ 沿 MN 折叠后,点 A 与 A’ 重合.
于是有P返回上一页下一页逆定理 如果两个图形的对应点连线被同一条直线垂
直平分,那么这两个图形关于这条直线对称.这个逆定理可以判定两个图形是否关于某直线对称,
它是作对称图形的主要依据. 返回 已知:如图,直线 l 及直线外一点 P.
求作:点 P’ ,使它与点 P 关于直线 l 对称.例 1 作法: POQP’1. 过点 P 作 PQ ⊥l ,交 l 与点 O . 2. 在直线 PQ 上,取 OP’ = OP . 点 P’ 为所作的点 .l上一页下一页返回巩固练习1.已知:如图,点 P 在直线 l 上,则
点 P 关于直线 l 的对称点在什么地方?(第1题)2.已知:如图,两点 A、B. 求作:
直线 l ,使点 A、B 关于直线 l 对称.AB(第2题)返回上一页下一页巩固练习3.已知: △ABC ≌△A’B’C’ , 那么 △ABC 与△A’B’C’
一定关于某直线对称吗?如果 △ABC 与△A’B’C’ 关于某直线对称,那么它们全等吗?为什么?4. 已知:如图, MN 垂直平分线段
AB 、CD,垂足分别是 E、F .
求证: AB = CD,∠ ACD= ∠ BDC .(提示:可用对称关系来证.)上一页下一页返回上一页下一页 水泵站修在什么地方?如图所示,水泵站修在 C 点可使所用的水管最短. 如图,要在河边修建一个水泵站,分别向张村、李庄送水,修在河边什么地方,可使所用的水管最短?张村李庄A’C返回应用新知小 结1、 要掌握轴对称变换的概念.2、 要掌握关于一条直线对称的两个图形的性质和判定,并会画出一个点的对称点.3、 除定义外,有什么方法可以判定两个图形成轴对称?上一页下一页返回作业P 135第1、2、4题 谢谢!
