2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册3.3.1 抛物线及其标准方程 课件(共27张PPT)
文档属性
| 名称 | 2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册3.3.1 抛物线及其标准方程 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 742.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-21 14:36:46 | ||
图片预览








文档简介
(共27张PPT)
3.3.1 抛物线及其标准方程
汇报日期
单/击/此/处/添/加/副/标/题/内/容
知识归纳
一、抛物线的定义
平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线,点F叫做抛物线的焦点,直线l 叫做抛物线的准线。{ =点M到直线的距离} (一动三定)
一、抛物线的定义
平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线,点F叫做抛物线的焦点,直线l 叫做抛物线的准线。{ =点M到直线的距离} (一动三定)
(注:定点F不在定直线上,否则动点的轨迹是过定点F垂直于直线l 的一条直线)
(一焦一顶一轴一准无心,也叫无心圆锥曲线); p是焦点F到l 的距离,p越大开口越大,反之越小。
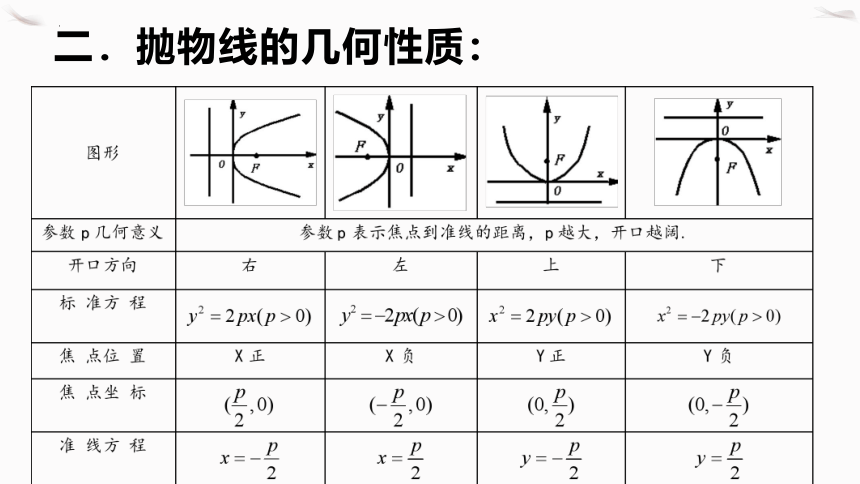
二.抛物线的几何性质:
定义辨析
求轨迹
求焦点或准线
1
2
3
目录
考点1:抛物线定义辨析
例1.在平面上,一动点到一定点的距离与它到一定直线的距离之比为1,则动点的轨迹是( )
A.抛物线 B.直线
C.抛物线或直线 D.以上结论均不正确
【详解】
一动点到一定点的距离与它到一定直线的距离之比为1,可得该动点到定点和定直线距离相等,
当定点不在定直线上时,动点的轨迹是抛物线;
当定点在定直线上时,动点的轨迹是经过该定点且垂直于定直线的直线;
故选C.
方法技巧
根据题意,
分定点不在定直线上和
定点在定直线上,两种情况分类讨论,结合抛物线的定义,即可求解.
变式训练
1.抛物线W: 的焦点为F.对于W上一点P,若P到直线的距离是P到点F距离的2倍,则点P的横坐标为( )
A.1 B.2 C.3 D.4
考点2:求抛物线的轨迹
例2.若点 满足方程 ,
则点P的轨迹是______.
方法技巧
根据轨迹方程所代表的意义判断点的轨迹满足曲线的定义.
【变式训练】
1.已知点F是拋物线C: x2=2py (p>0) 的焦点,P(x0 ,1)是上的一点, ,则( )
A.2 B.4 C.6 D.8
【详解】
由抛物线的定义可知, ,所以 .
2.若抛物线的焦点是 F(1,0) ,准线方为 X=-1 ,则抛物线的标准方程是______.
3.已知抛物线 y2=2px (p>0)上的两点A、B到焦点的距离之和为5,线段AB的中点的横坐标是2,则p=______.
考点3:抛物线求焦点或准线
例3.已知抛物线x2=2my (m>0)上的点(x0,1)到该抛物线焦点F的距离为2,则m=( )
A.1 B.2 C.4 D.6
方法技巧
根据抛物线的标准方程,得到准线方程与焦点坐标,根据抛物线的定义,可列方程,得到答案.
【变式训练】
1.与抛物线x2=4y关于直线x+y=0对称的抛物线的焦点坐标是______.
2、已知圆x2+(y-1)2=m与抛物线x2=4y的准线相切,则m=___________.
谢谢聆听
单击此处添加文本具体内容
3.3.1 抛物线及其标准方程
汇报日期
单/击/此/处/添/加/副/标/题/内/容
知识归纳
一、抛物线的定义
平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线,点F叫做抛物线的焦点,直线l 叫做抛物线的准线。{ =点M到直线的距离} (一动三定)
一、抛物线的定义
平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线,点F叫做抛物线的焦点,直线l 叫做抛物线的准线。{ =点M到直线的距离} (一动三定)
(注:定点F不在定直线上,否则动点的轨迹是过定点F垂直于直线l 的一条直线)
(一焦一顶一轴一准无心,也叫无心圆锥曲线); p是焦点F到l 的距离,p越大开口越大,反之越小。
二.抛物线的几何性质:
定义辨析
求轨迹
求焦点或准线
1
2
3
目录
考点1:抛物线定义辨析
例1.在平面上,一动点到一定点的距离与它到一定直线的距离之比为1,则动点的轨迹是( )
A.抛物线 B.直线
C.抛物线或直线 D.以上结论均不正确
【详解】
一动点到一定点的距离与它到一定直线的距离之比为1,可得该动点到定点和定直线距离相等,
当定点不在定直线上时,动点的轨迹是抛物线;
当定点在定直线上时,动点的轨迹是经过该定点且垂直于定直线的直线;
故选C.
方法技巧
根据题意,
分定点不在定直线上和
定点在定直线上,两种情况分类讨论,结合抛物线的定义,即可求解.
变式训练
1.抛物线W: 的焦点为F.对于W上一点P,若P到直线的距离是P到点F距离的2倍,则点P的横坐标为( )
A.1 B.2 C.3 D.4
考点2:求抛物线的轨迹
例2.若点 满足方程 ,
则点P的轨迹是______.
方法技巧
根据轨迹方程所代表的意义判断点的轨迹满足曲线的定义.
【变式训练】
1.已知点F是拋物线C: x2=2py (p>0) 的焦点,P(x0 ,1)是上的一点, ,则( )
A.2 B.4 C.6 D.8
【详解】
由抛物线的定义可知, ,所以 .
2.若抛物线的焦点是 F(1,0) ,准线方为 X=-1 ,则抛物线的标准方程是______.
3.已知抛物线 y2=2px (p>0)上的两点A、B到焦点的距离之和为5,线段AB的中点的横坐标是2,则p=______.
考点3:抛物线求焦点或准线
例3.已知抛物线x2=2my (m>0)上的点(x0,1)到该抛物线焦点F的距离为2,则m=( )
A.1 B.2 C.4 D.6
方法技巧
根据抛物线的标准方程,得到准线方程与焦点坐标,根据抛物线的定义,可列方程,得到答案.
【变式训练】
1.与抛物线x2=4y关于直线x+y=0对称的抛物线的焦点坐标是______.
2、已知圆x2+(y-1)2=m与抛物线x2=4y的准线相切,则m=___________.
谢谢聆听
单击此处添加文本具体内容
