3.4 二元一次方程组的应用(2)课件(共22张PPT)
文档属性
| 名称 | 3.4 二元一次方程组的应用(2)课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 956.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-21 16:01:01 | ||
图片预览







文档简介
(共22张PPT)
沪科版 七年级上册
3.4 二元一次方程组的应用(2)
教学目标
会借助表格对实际问题中的数量关系进行分析、整理,列出方程组解决问题.
教学重点:设计适当的表格,帮助分析、整理问题中的数量关系;
教学难点:根据问题特点,正确设计表格,形成分析问题的一般性策略.
用二元一次方程组解决问题的简单步骤和方法:
1.理解题意,找出表示实际问题意义的两个
相等关系;
2.设两个未知数,再根据相等关系列出方程组;
3.解这个方程组,并写出答案.
复习旧知
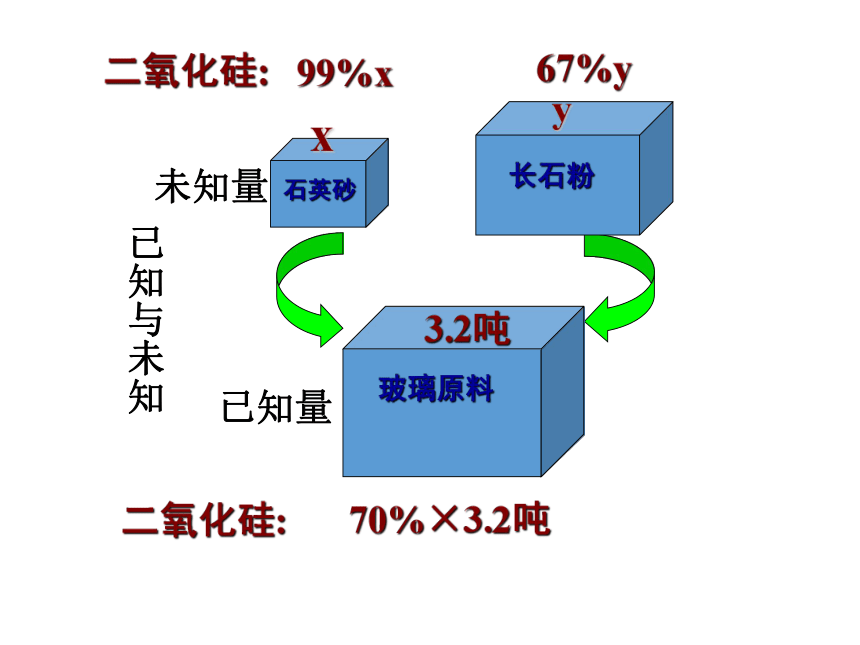
例3 玻璃厂熔炼玻璃液,原料是石英砂和长石粉混合而成,要求原料中含二氧化硅70%.根据化验,石英砂中含二氧化硅99%,长石粉中含二氧化硅67%.试问在3.2t原料中,石英砂和长石粉各多少吨?
分析:
1.问题中涉及到了哪些已知量和未知量?
2.这些量之间有何关系?
例题解析
玻璃原料
3.2吨
67%y
石英砂
x
长石粉
y
二氧化硅:
99%x
70%×3.2吨
已知与未知
已知量
未知量
二氧化硅:
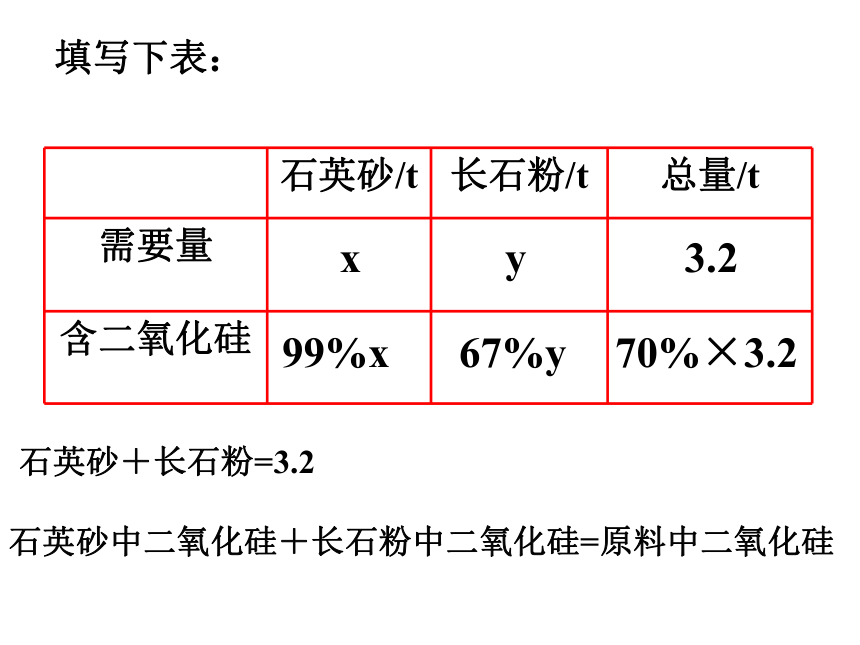
石英砂/t 长石粉/t 总量/t
需要量
含二氧化硅
填写下表:
x
y
3.2
99%x
67%y
70%×3.2
石英砂+长石粉=3.2
石英砂中二氧化硅+长石粉中二氧化硅=原料中二氧化硅
解:设需要石英砂x t,长石粉y t.
根据题意,得
x+y=3.2 ①
99%x+67%y=70%×3.2 ②
例3 玻璃厂熔炼玻璃液,原料是石英砂和长石粉混合而成,要求原料中含二氧化硅70%.根据化验,石英砂中含二氧化硅99%,长石粉中含二氧化硅67%.试问在3.2t原料中,石英砂和长石粉各多少吨?
石英砂+长石粉=3.2
石英砂中二氧化硅+长石粉中二氧化硅=原料中二氧化硅
99%x
67%y
70%×3.2
解:设需要石英砂x t,长石粉y t.
根据题意,得
x+y=3.2 ①
99%x+67%y=70%×3.2 ②
例3 玻璃厂熔炼玻璃液,原料是石英砂和长石粉混合而成,要求原料中含二氧化硅70%.根据化验,石英砂中含二氧化硅99%,长石粉中含二氧化硅67%.试问在3.2t原料中,石英砂和长石粉各多少吨?
99x+67y=70×3.2
67x+67y=67×3.2
32x=3×3.2
③
④
⑤
x=0.3
解:设需要石英砂x t,长石粉y t.
解方程组,得
答:在3.2 t原料中,石英砂0.3 t,长石粉2.9 t.
根据题意,得
x+y=3.2 ①
99%x+67%y=70%×3.2 ②
x=
y=
0.3,
2.9.
例3 玻璃厂熔炼玻璃液,原料是石英砂和长石粉混合而成,要求原料中含二氧化硅70%.根据化验,石英砂中含二氧化硅99%,长石粉中含二氧化硅67%.试问在3.2t原料中,石英砂和长石粉各多少吨?
1.某乡今年春播作物的面积比秋播作物的面积多630hm2,
计划明年春播作物的面积增加20%,秋播作物的面积减
少10%,这样明年春、秋作物的总面积将比今年增加
12%.试求这个乡今年春播与秋播作物的面积各是多少?
解:设今年春播作物面积为x hm2,秋播作物面积为y hm2.
根据题意,得
x- y=630 ①
(1+20%)x+(1-10%)y=(1+12%)(x+y) ②
今年春播作物面积-今年秋播作物面积=630
明年春播面积+明年秋播面积=今年面积增加12%
1.某乡今年春播作物的面积比秋播作物的面积多630hm2,
计划明年春播作物的面积增加20%,秋播作物的面积减
少10%,这样明年春、秋作物的总面积将比今年增加
12%.试求这个乡今年春播与秋播作物的面积各是多少?
解:设今年春播作物面积为x hm2,秋播作物面积为y hm2.
根据题意,得
x-y=630 ①
(1+20%)x+(1-10%)y=(1+12%)(x+y) ②
0.08x-0.22y=0
22x-22y=22×630
14x=22×630
x=990
③
④
⑤
8x-22y=0
1.某乡今年春播作物的面积比秋播作物的面积多630hm2,
计划明年春播作物的面积增加20%,秋播作物的面积减
少10%,这样明年春、秋作物的总面积将比今年增加
12%.试求这个乡今年春播与秋播作物的面积各是多少?
解:设今年春播作物面积为x hm2,秋播作物面积为y hm2.
根据题意,得
解方程组,得
答:
x- y=630 ①
x=
y=
990,
360.
今年春播作物面积为990hm2,秋播作物面积为360hm2.
(1+20%)x+(1-10%)y=(1+12%)(x+y) ②
2.甲、乙两种铜块分别含铜60%和80%.请
问这两种铜块各取多少克,熔化后才能得
到含铜74%的铜块500克.
解:设甲种铜取x克,乙种铜取y克.
根据题意,得
x+y=500 ①
60%x+80%y=74%×500 ②
甲种铜块+乙种铜块=500
甲种铜块中的铜+乙种铜块中铜=500克铜块中的铜
60%x
80%y
74%×500
2.甲、乙两种铜块分别含铜60%和80%.请
问这两种铜块各取多少克,熔化后才能得
到含铜74%的铜块500克.
解:设甲种铜取x克,乙种铜取y克.
根据题意,得
x+y=500 ①
60%x+80%y=74%×500 ②
60x+80y=74×500
6x+8y=7.4×500
6x+6y=6×500
2y=1.4×500
y=350
③
④
⑤
2.甲、乙两种铜块分别含铜60%和80%.请
问这两种铜块各取多少克,熔化后才能得
到含铜74%的铜块500克.
解:设甲种铜取x克,乙种铜取y克.
解方程组,得
答:甲种铜取150克,乙种铜取350克.
根据题意,得
x+y=500 ①
60%x+80%y=74%×500 ②
x=
y=
150,
350.
回顾本课的学习过程,回答以下问题:
1. 你能弄懂配比问题了吗?
2. 如何通过表格归纳实际问题?
3. 借助表格分析实际问题,对列方程有
什么作用?
课堂小结
1. 如图,10块相同的长方形墙砖拼成一个矩形,
设长方形墙砖的长和宽分别为x厘米和y厘米,
则依题意列方程组正确的是( )
B.
x+2y=75
x=3y
A.
x+2y=75
y=3x
D.
2x+y=75
x=3y
C.
2x+y=75
y=3x
练习巩固
B
2.陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( )
A.19 B.18 C.16 D.15
C
3.一张方桌由一个桌面和四个桌腿组成,如果1立方米木料可制作方桌桌面50个,或制作桌腿300条,现有5立方米木料,请你设计一下,用多少木料做桌面,用多少木料做桌腿,恰好制成方桌多少张?
解:设用x立方米木料做桌面,y立方米木料做桌腿,
x+y = 5
根据题意,得
50x
解方程组得
x=
y=
300y
=
4
2
3
答:设用3立方米木料做桌面,2立方米木料做桌腿.
今天作业
课本P112页第1、2、5 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级上册
3.4 二元一次方程组的应用(2)
教学目标
会借助表格对实际问题中的数量关系进行分析、整理,列出方程组解决问题.
教学重点:设计适当的表格,帮助分析、整理问题中的数量关系;
教学难点:根据问题特点,正确设计表格,形成分析问题的一般性策略.
用二元一次方程组解决问题的简单步骤和方法:
1.理解题意,找出表示实际问题意义的两个
相等关系;
2.设两个未知数,再根据相等关系列出方程组;
3.解这个方程组,并写出答案.
复习旧知
例3 玻璃厂熔炼玻璃液,原料是石英砂和长石粉混合而成,要求原料中含二氧化硅70%.根据化验,石英砂中含二氧化硅99%,长石粉中含二氧化硅67%.试问在3.2t原料中,石英砂和长石粉各多少吨?
分析:
1.问题中涉及到了哪些已知量和未知量?
2.这些量之间有何关系?
例题解析
玻璃原料
3.2吨
67%y
石英砂
x
长石粉
y
二氧化硅:
99%x
70%×3.2吨
已知与未知
已知量
未知量
二氧化硅:
石英砂/t 长石粉/t 总量/t
需要量
含二氧化硅
填写下表:
x
y
3.2
99%x
67%y
70%×3.2
石英砂+长石粉=3.2
石英砂中二氧化硅+长石粉中二氧化硅=原料中二氧化硅
解:设需要石英砂x t,长石粉y t.
根据题意,得
x+y=3.2 ①
99%x+67%y=70%×3.2 ②
例3 玻璃厂熔炼玻璃液,原料是石英砂和长石粉混合而成,要求原料中含二氧化硅70%.根据化验,石英砂中含二氧化硅99%,长石粉中含二氧化硅67%.试问在3.2t原料中,石英砂和长石粉各多少吨?
石英砂+长石粉=3.2
石英砂中二氧化硅+长石粉中二氧化硅=原料中二氧化硅
99%x
67%y
70%×3.2
解:设需要石英砂x t,长石粉y t.
根据题意,得
x+y=3.2 ①
99%x+67%y=70%×3.2 ②
例3 玻璃厂熔炼玻璃液,原料是石英砂和长石粉混合而成,要求原料中含二氧化硅70%.根据化验,石英砂中含二氧化硅99%,长石粉中含二氧化硅67%.试问在3.2t原料中,石英砂和长石粉各多少吨?
99x+67y=70×3.2
67x+67y=67×3.2
32x=3×3.2
③
④
⑤
x=0.3
解:设需要石英砂x t,长石粉y t.
解方程组,得
答:在3.2 t原料中,石英砂0.3 t,长石粉2.9 t.
根据题意,得
x+y=3.2 ①
99%x+67%y=70%×3.2 ②
x=
y=
0.3,
2.9.
例3 玻璃厂熔炼玻璃液,原料是石英砂和长石粉混合而成,要求原料中含二氧化硅70%.根据化验,石英砂中含二氧化硅99%,长石粉中含二氧化硅67%.试问在3.2t原料中,石英砂和长石粉各多少吨?
1.某乡今年春播作物的面积比秋播作物的面积多630hm2,
计划明年春播作物的面积增加20%,秋播作物的面积减
少10%,这样明年春、秋作物的总面积将比今年增加
12%.试求这个乡今年春播与秋播作物的面积各是多少?
解:设今年春播作物面积为x hm2,秋播作物面积为y hm2.
根据题意,得
x- y=630 ①
(1+20%)x+(1-10%)y=(1+12%)(x+y) ②
今年春播作物面积-今年秋播作物面积=630
明年春播面积+明年秋播面积=今年面积增加12%
1.某乡今年春播作物的面积比秋播作物的面积多630hm2,
计划明年春播作物的面积增加20%,秋播作物的面积减
少10%,这样明年春、秋作物的总面积将比今年增加
12%.试求这个乡今年春播与秋播作物的面积各是多少?
解:设今年春播作物面积为x hm2,秋播作物面积为y hm2.
根据题意,得
x-y=630 ①
(1+20%)x+(1-10%)y=(1+12%)(x+y) ②
0.08x-0.22y=0
22x-22y=22×630
14x=22×630
x=990
③
④
⑤
8x-22y=0
1.某乡今年春播作物的面积比秋播作物的面积多630hm2,
计划明年春播作物的面积增加20%,秋播作物的面积减
少10%,这样明年春、秋作物的总面积将比今年增加
12%.试求这个乡今年春播与秋播作物的面积各是多少?
解:设今年春播作物面积为x hm2,秋播作物面积为y hm2.
根据题意,得
解方程组,得
答:
x- y=630 ①
x=
y=
990,
360.
今年春播作物面积为990hm2,秋播作物面积为360hm2.
(1+20%)x+(1-10%)y=(1+12%)(x+y) ②
2.甲、乙两种铜块分别含铜60%和80%.请
问这两种铜块各取多少克,熔化后才能得
到含铜74%的铜块500克.
解:设甲种铜取x克,乙种铜取y克.
根据题意,得
x+y=500 ①
60%x+80%y=74%×500 ②
甲种铜块+乙种铜块=500
甲种铜块中的铜+乙种铜块中铜=500克铜块中的铜
60%x
80%y
74%×500
2.甲、乙两种铜块分别含铜60%和80%.请
问这两种铜块各取多少克,熔化后才能得
到含铜74%的铜块500克.
解:设甲种铜取x克,乙种铜取y克.
根据题意,得
x+y=500 ①
60%x+80%y=74%×500 ②
60x+80y=74×500
6x+8y=7.4×500
6x+6y=6×500
2y=1.4×500
y=350
③
④
⑤
2.甲、乙两种铜块分别含铜60%和80%.请
问这两种铜块各取多少克,熔化后才能得
到含铜74%的铜块500克.
解:设甲种铜取x克,乙种铜取y克.
解方程组,得
答:甲种铜取150克,乙种铜取350克.
根据题意,得
x+y=500 ①
60%x+80%y=74%×500 ②
x=
y=
150,
350.
回顾本课的学习过程,回答以下问题:
1. 你能弄懂配比问题了吗?
2. 如何通过表格归纳实际问题?
3. 借助表格分析实际问题,对列方程有
什么作用?
课堂小结
1. 如图,10块相同的长方形墙砖拼成一个矩形,
设长方形墙砖的长和宽分别为x厘米和y厘米,
则依题意列方程组正确的是( )
B.
x+2y=75
x=3y
A.
x+2y=75
y=3x
D.
2x+y=75
x=3y
C.
2x+y=75
y=3x
练习巩固
B
2.陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( )
A.19 B.18 C.16 D.15
C
3.一张方桌由一个桌面和四个桌腿组成,如果1立方米木料可制作方桌桌面50个,或制作桌腿300条,现有5立方米木料,请你设计一下,用多少木料做桌面,用多少木料做桌腿,恰好制成方桌多少张?
解:设用x立方米木料做桌面,y立方米木料做桌腿,
x+y = 5
根据题意,得
50x
解方程组得
x=
y=
300y
=
4
2
3
答:设用3立方米木料做桌面,2立方米木料做桌腿.
今天作业
课本P112页第1、2、5 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
