贵州省贵阳市第十九中学2020-2021学年九年级下学期3月月考数学试卷(含答案)
文档属性
| 名称 | 贵州省贵阳市第十九中学2020-2021学年九年级下学期3月月考数学试卷(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-21 00:00:00 | ||
图片预览



文档简介
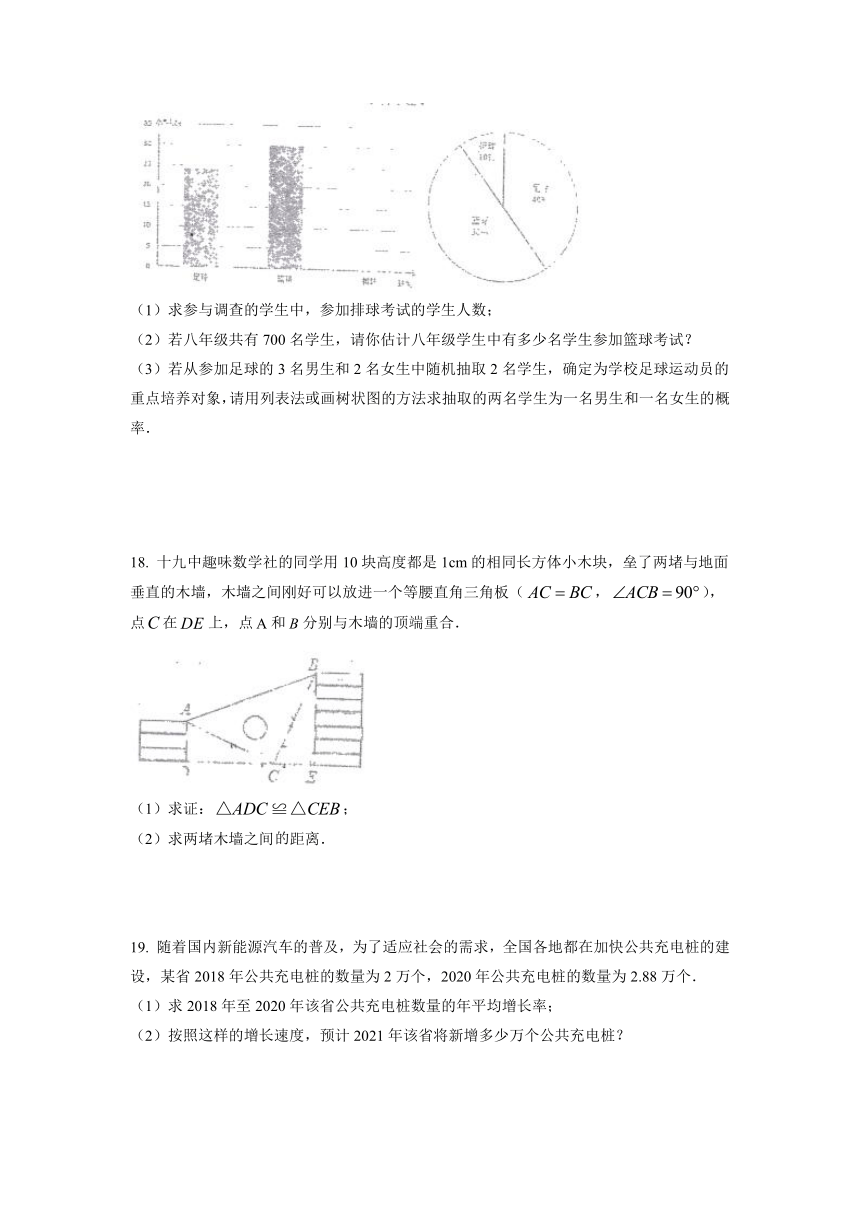
贵州省贵阳市第十九中学2020-2021学年九年级下学期3月月考数学试卷
一、选择题(共12小题,满分36分,每小题3分)
1. 贵阳某日最高气温为13℃,最低气温为3℃,则这天温差为( )
A. 16 B. 10 C. 13 D. 3
2. 如图,直线,交于点,射线平分,如果,那么等于( )
A. 38° B. 104° C. 142° D. 76°
3. 新型冠状病毒疫情发生以来,截止2021年3月15日全球共有1亿2千万人感染.数据1亿2千万可以表示为( )
A. B. C. D.
4. 由6个大小相同的正方体搭成的几何体如图所示,比较从三个不同方向看到的平面图形的面积,则( )
A. 从三个不同方向看到的平面图形的面积一样大
B. 从正面看到的平面图形面积最小
C. 从左面看到平面图形的面积最小
D. 从上面看到的平面图形的面积最小
5. 下列各点在一次函数的图象上的是( )
A. B. C. D.
6. 甲、乙两人各自掷一个普通的正方体骰子,如果两者之和为偶数,甲得1分;如果两者之和为奇数,乙得1分,此游戏( )
A. 是公平的 B. 对乙有利 C. 对甲有利 D. 以上都不对
7. 如图,菱形的对角线、相交于点,,,则边的长为( )
A. 4 B. C. 2 D.
8. 不等式组的解集是,则可能的值是( )
A. 3 B. 4 C. 5 D. 6
9. 如图,四边形内接于,为直径,,连接,若,则的度数为( )
A. 50° B. 65° C. 75° D. 130°
10. 若把,值同时缩小为原来的倍,则下列分式的值保持不变的是( )
A. B. C. D.
11. 如图,中,,,的值为,则( )
A. B. C. D.
12. 在平面直角坐标系中,若点P的横坐标和纵坐标相等,则称点P为完美点.已知二次函数的图象上有且只有一个完美点,且当时,函数的最小值为最大值为1,则m的取值范围是( )
A. B. C. D.
二、填空题(共4小题,满分16分,每小题4分)
13. 已知是方程的解,则__________.
14. 已知反比例函数,若时,,则的取值范围__________.
15. 如图,在中,,以为边在外作等边,过点作,垂足为,若,,则的长为___________.
16. 如图,在矩形中,点为边上不与、重合的一个动点,过点作交于点,交于点,以为对称轴折叠矩形,点、的对应点分别是、,连接、,若,,当为直角三角形时,的长为___________.
三、解答题(共9小题,满分98分)
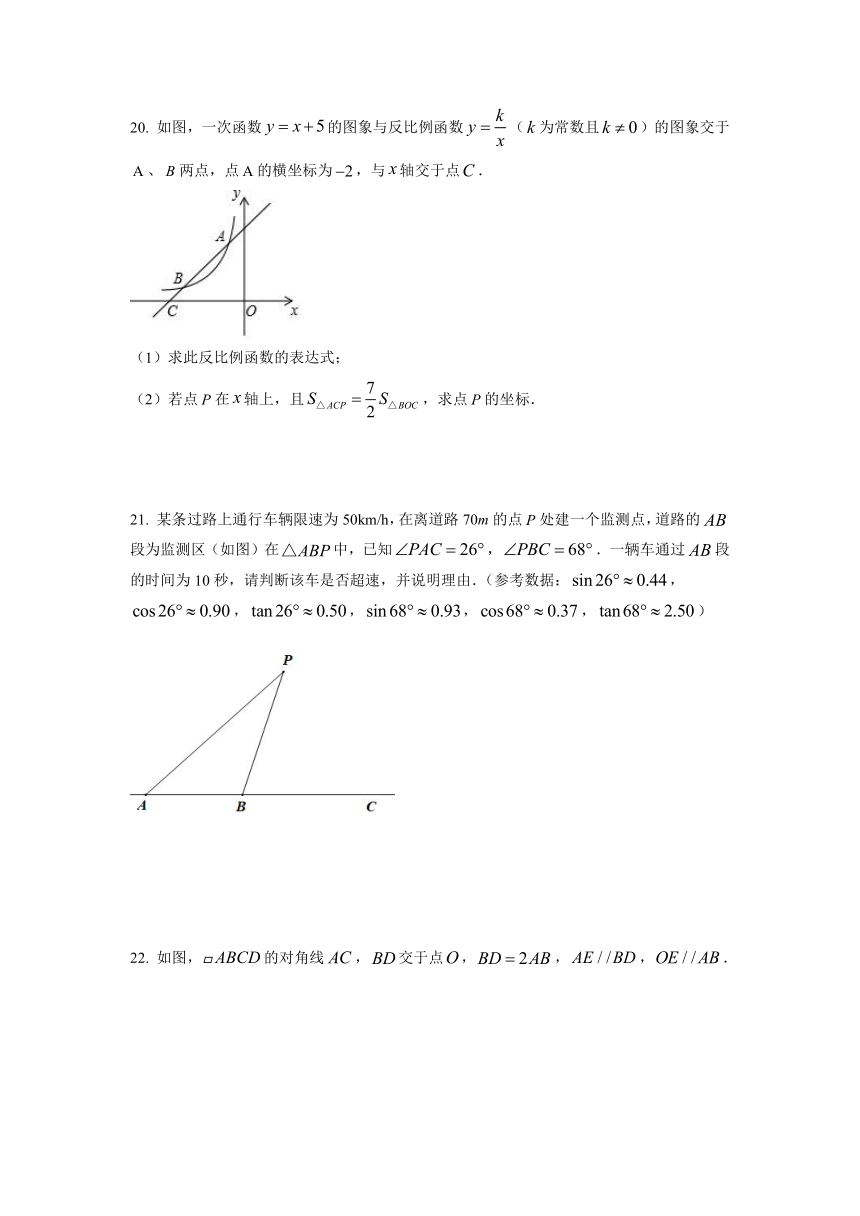
17. 贵阳第十九中学八年级学生参加体育中考,现从八年级学生中抽取部分学生进行问卷调查,通过分析整理绘制了如图两幅统计图,请根据两幅统计图中信息回答下列问题:
(1)求参与调查的学生中,参加排球考试的学生人数;
(2)若八年级共有700名学生,请你估计八年级学生中有多少名学生参加篮球考试?
(3)若从参加足球的3名男生和2名女生中随机抽取2名学生,确定为学校足球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.
18. 十九中趣味数学社的同学用10块高度都是1cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点在上,点和分别与木墙的顶端重合.
(1)求证:;
(2)求两堵木墙之间距离.
19. 随着国内新能源汽车的普及,为了适应社会的需求,全国各地都在加快公共充电桩的建设,某省2018年公共充电桩的数量为2万个,2020年公共充电桩的数量为2.88万个.
(1)求2018年至2020年该省公共充电桩数量的年平均增长率;
(2)按照这样的增长速度,预计2021年该省将新增多少万个公共充电桩?
20. 如图,一次函数的图象与反比例函数(为常数且)的图象交于、两点,点的横坐标为,与轴交于点.
(1)求此反比例函数的表达式;
(2)若点在轴上,且,求点的坐标.
21. 某条过路上通行车辆限速为50km/h,在离道路70m的点处建一个监测点,道路的段为监测区(如图)在中,已知,.一辆车通过段的时间为10秒,请判断该车是否超速,并说明理由.(参考数据:,,,,,)
22. 如图,的对角线,交于点,,,.
(1)求证:四边形是菱形;
(2)若,,求的长.
23. 如图,以为直径的经过的中点,于点.
(1)求证:是的切线;
(2)当,时,求图中阴影部分的面积(结果保留根号和).
24. 甲乙两人先后从地出发沿同一直道去地.设乙出发第时,甲、乙离地的距离分别为,,与之间的函数表达式是,与之间的函数表达式是.
(1)乙出发时,甲离地的距离为____________m.
(2)乙出发至甲到达地这段时间内,
①两人何时相距180m?
②两人何时相距最近?最近距离是多少?
25. 在与中,,,,连接,点为的中点,连接,绕着点旋转.
(1)如图1,当点落在的延长线上时,与的数量关系是:__________;
(2)如图2,当旋转到点落在的延长线上时,与是否仍有具有(1)中的数量关系,如果具有,请给予证明;如果没有,请说明理由;
(3)旋转过程中,若当时,直接写出的值.
贵州省贵阳市第十九中学2020-2021学年九年级下学期3月月考数学试卷
一、选择题(共12小题,满分36分,每小题3分)
1. 贵阳某日最高气温为13℃,最低气温为3℃,则这天温差为( )
A. 16 B. 10 C. 13 D. 3
【答案】B
2. 如图,直线,交于点,射线平分,如果,那么等于( )
A. 38° B. 104° C. 142° D. 76°
【答案】D
3. 新型冠状病毒疫情发生以来,截止2021年3月15日全球共有1亿2千万人感染.数据1亿2千万可以表示为( )
A. B. C. D.
【答案】B
4. 由6个大小相同的正方体搭成的几何体如图所示,比较从三个不同方向看到的平面图形的面积,则( )
A. 从三个不同方向看到的平面图形的面积一样大
B. 从正面看到的平面图形面积最小
C. 从左面看到平面图形的面积最小
D. 从上面看到的平面图形的面积最小
【答案】C
5. 下列各点在一次函数的图象上的是( )
A. B. C. D.
【答案】D
6. 甲、乙两人各自掷一个普通的正方体骰子,如果两者之和为偶数,甲得1分;如果两者之和为奇数,乙得1分,此游戏( )
A. 是公平的 B. 对乙有利 C. 对甲有利 D. 以上都不对
【答案】C
7. 如图,菱形的对角线、相交于点,,,则边的长为( )
A. 4 B. C. 2 D.
【答案】A
8. 不等式组的解集是,则可能的值是( )
A. 3 B. 4 C. 5 D. 6
【答案】A
9. 如图,四边形内接于,为直径,,连接,若,则的度数为( )
A. 50° B. 65° C. 75° D. 130°
【答案】B
10. 若把,值同时缩小为原来的倍,则下列分式的值保持不变的是( )
A. B. C. D.
【答案】C
11. 如图,中,,,的值为,则( )
A. B. C. D.
【答案】D
12. 在平面直角坐标系中,若点P的横坐标和纵坐标相等,则称点P为完美点.已知二次函数的图象上有且只有一个完美点,且当时,函数的最小值为最大值为1,则m的取值范围是( )
A. B. C. D.
【答案】B
二、填空题(共4小题,满分16分,每小题4分)
13. 已知是方程的解,则__________.
【答案】
14. 已知反比例函数,若时,,则的取值范围__________.
【答案】
15. 如图,在中,,以为边在外作等边,过点作,垂足为,若,,则的长为___________.
【答案】8
16. 如图,在矩形中,点为边上不与、重合的一个动点,过点作交于点,交于点,以为对称轴折叠矩形,点、的对应点分别是、,连接、,若,,当为直角三角形时,的长为___________.
【答案】或
三、解答题(共9小题,满分98分)
17. 贵阳第十九中学八年级学生参加体育中考,现从八年级学生中抽取部分学生进行问卷调查,通过分析整理绘制了如图两幅统计图,请根据两幅统计图中信息回答下列问题:
(1)求参与调查的学生中,参加排球考试的学生人数;
(2)若八年级共有700名学生,请你估计八年级学生中有多少名学生参加篮球考试?
(3)若从参加足球的3名男生和2名女生中随机抽取2名学生,确定为学校足球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.
【答案】(1)6;(2)350;(3)
18. 十九中趣味数学社的同学用10块高度都是1cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点在上,点和分别与木墙的顶端重合.
(1)求证:;
(2)求两堵木墙之间距离.
【答案】(1)见详解;(2)
19. 随着国内新能源汽车的普及,为了适应社会的需求,全国各地都在加快公共充电桩的建设,某省2018年公共充电桩的数量为2万个,2020年公共充电桩的数量为2.88万个.
(1)求2018年至2020年该省公共充电桩数量的年平均增长率;
(2)按照这样的增长速度,预计2021年该省将新增多少万个公共充电桩?
【答案】(1)2018年至2020年该省公共充电桩数量的年平均增长率为20%.(2)预计2021年该省将新增0.576万个公共充电桩.
20. 如图,一次函数的图象与反比例函数(为常数且)的图象交于、两点,点的横坐标为,与轴交于点.
(1)求此反比例函数的表达式;
(2)若点在轴上,且,求点的坐标.
【答案】(1)反比例函数的表达式为;(2)点P(-,0)或(,0).
21. 某条过路上通行车辆限速为50km/h,在离道路70m的点处建一个监测点,道路的段为监测区(如图)在中,已知,.一辆车通过段的时间为10秒,请判断该车是否超速,并说明理由.(参考数据:,,,,,)
【答案】没有超速,理由见解析
22. 如图,的对角线,交于点,,,.
(1)求证:四边形是菱形;
(2)若,,求的长.
【答案】(1)见解析;(2)2
23. 如图,以为直径的经过的中点,于点.
(1)求证:是的切线;
(2)当,时,求图中阴影部分的面积(结果保留根号和).
【答案】(1)见解析;(2)
24. 甲乙两人先后从地出发沿同一直道去地.设乙出发第时,甲、乙离地的距离分别为,,与之间的函数表达式是,与之间的函数表达式是.
(1)乙出发时,甲离地的距离为____________m.
(2)乙出发至甲到达地这段时间内,
①两人何时相距180m?
②两人何时相距最近?最近距离是多少?
【答案】(1)250;(2)①1min或7min;②当乙出发第4min时,两人相距最近,最近距离是90m
25. 在与中,,,,连接,点为的中点,连接,绕着点旋转.
(1)如图1,当点落在的延长线上时,与的数量关系是:__________;
(2)如图2,当旋转到点落在的延长线上时,与是否仍有具有(1)中的数量关系,如果具有,请给予证明;如果没有,请说明理由;
(3)旋转过程中,若当时,直接写出的值.
【答案】(1);(2)具有,证明见解析;(3)14或.
一、选择题(共12小题,满分36分,每小题3分)
1. 贵阳某日最高气温为13℃,最低气温为3℃,则这天温差为( )
A. 16 B. 10 C. 13 D. 3
2. 如图,直线,交于点,射线平分,如果,那么等于( )
A. 38° B. 104° C. 142° D. 76°
3. 新型冠状病毒疫情发生以来,截止2021年3月15日全球共有1亿2千万人感染.数据1亿2千万可以表示为( )
A. B. C. D.
4. 由6个大小相同的正方体搭成的几何体如图所示,比较从三个不同方向看到的平面图形的面积,则( )
A. 从三个不同方向看到的平面图形的面积一样大
B. 从正面看到的平面图形面积最小
C. 从左面看到平面图形的面积最小
D. 从上面看到的平面图形的面积最小
5. 下列各点在一次函数的图象上的是( )
A. B. C. D.
6. 甲、乙两人各自掷一个普通的正方体骰子,如果两者之和为偶数,甲得1分;如果两者之和为奇数,乙得1分,此游戏( )
A. 是公平的 B. 对乙有利 C. 对甲有利 D. 以上都不对
7. 如图,菱形的对角线、相交于点,,,则边的长为( )
A. 4 B. C. 2 D.
8. 不等式组的解集是,则可能的值是( )
A. 3 B. 4 C. 5 D. 6
9. 如图,四边形内接于,为直径,,连接,若,则的度数为( )
A. 50° B. 65° C. 75° D. 130°
10. 若把,值同时缩小为原来的倍,则下列分式的值保持不变的是( )
A. B. C. D.
11. 如图,中,,,的值为,则( )
A. B. C. D.
12. 在平面直角坐标系中,若点P的横坐标和纵坐标相等,则称点P为完美点.已知二次函数的图象上有且只有一个完美点,且当时,函数的最小值为最大值为1,则m的取值范围是( )
A. B. C. D.
二、填空题(共4小题,满分16分,每小题4分)
13. 已知是方程的解,则__________.
14. 已知反比例函数,若时,,则的取值范围__________.
15. 如图,在中,,以为边在外作等边,过点作,垂足为,若,,则的长为___________.
16. 如图,在矩形中,点为边上不与、重合的一个动点,过点作交于点,交于点,以为对称轴折叠矩形,点、的对应点分别是、,连接、,若,,当为直角三角形时,的长为___________.
三、解答题(共9小题,满分98分)
17. 贵阳第十九中学八年级学生参加体育中考,现从八年级学生中抽取部分学生进行问卷调查,通过分析整理绘制了如图两幅统计图,请根据两幅统计图中信息回答下列问题:
(1)求参与调查的学生中,参加排球考试的学生人数;
(2)若八年级共有700名学生,请你估计八年级学生中有多少名学生参加篮球考试?
(3)若从参加足球的3名男生和2名女生中随机抽取2名学生,确定为学校足球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.
18. 十九中趣味数学社的同学用10块高度都是1cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点在上,点和分别与木墙的顶端重合.
(1)求证:;
(2)求两堵木墙之间距离.
19. 随着国内新能源汽车的普及,为了适应社会的需求,全国各地都在加快公共充电桩的建设,某省2018年公共充电桩的数量为2万个,2020年公共充电桩的数量为2.88万个.
(1)求2018年至2020年该省公共充电桩数量的年平均增长率;
(2)按照这样的增长速度,预计2021年该省将新增多少万个公共充电桩?
20. 如图,一次函数的图象与反比例函数(为常数且)的图象交于、两点,点的横坐标为,与轴交于点.
(1)求此反比例函数的表达式;
(2)若点在轴上,且,求点的坐标.
21. 某条过路上通行车辆限速为50km/h,在离道路70m的点处建一个监测点,道路的段为监测区(如图)在中,已知,.一辆车通过段的时间为10秒,请判断该车是否超速,并说明理由.(参考数据:,,,,,)
22. 如图,的对角线,交于点,,,.
(1)求证:四边形是菱形;
(2)若,,求的长.
23. 如图,以为直径的经过的中点,于点.
(1)求证:是的切线;
(2)当,时,求图中阴影部分的面积(结果保留根号和).
24. 甲乙两人先后从地出发沿同一直道去地.设乙出发第时,甲、乙离地的距离分别为,,与之间的函数表达式是,与之间的函数表达式是.
(1)乙出发时,甲离地的距离为____________m.
(2)乙出发至甲到达地这段时间内,
①两人何时相距180m?
②两人何时相距最近?最近距离是多少?
25. 在与中,,,,连接,点为的中点,连接,绕着点旋转.
(1)如图1,当点落在的延长线上时,与的数量关系是:__________;
(2)如图2,当旋转到点落在的延长线上时,与是否仍有具有(1)中的数量关系,如果具有,请给予证明;如果没有,请说明理由;
(3)旋转过程中,若当时,直接写出的值.
贵州省贵阳市第十九中学2020-2021学年九年级下学期3月月考数学试卷
一、选择题(共12小题,满分36分,每小题3分)
1. 贵阳某日最高气温为13℃,最低气温为3℃,则这天温差为( )
A. 16 B. 10 C. 13 D. 3
【答案】B
2. 如图,直线,交于点,射线平分,如果,那么等于( )
A. 38° B. 104° C. 142° D. 76°
【答案】D
3. 新型冠状病毒疫情发生以来,截止2021年3月15日全球共有1亿2千万人感染.数据1亿2千万可以表示为( )
A. B. C. D.
【答案】B
4. 由6个大小相同的正方体搭成的几何体如图所示,比较从三个不同方向看到的平面图形的面积,则( )
A. 从三个不同方向看到的平面图形的面积一样大
B. 从正面看到的平面图形面积最小
C. 从左面看到平面图形的面积最小
D. 从上面看到的平面图形的面积最小
【答案】C
5. 下列各点在一次函数的图象上的是( )
A. B. C. D.
【答案】D
6. 甲、乙两人各自掷一个普通的正方体骰子,如果两者之和为偶数,甲得1分;如果两者之和为奇数,乙得1分,此游戏( )
A. 是公平的 B. 对乙有利 C. 对甲有利 D. 以上都不对
【答案】C
7. 如图,菱形的对角线、相交于点,,,则边的长为( )
A. 4 B. C. 2 D.
【答案】A
8. 不等式组的解集是,则可能的值是( )
A. 3 B. 4 C. 5 D. 6
【答案】A
9. 如图,四边形内接于,为直径,,连接,若,则的度数为( )
A. 50° B. 65° C. 75° D. 130°
【答案】B
10. 若把,值同时缩小为原来的倍,则下列分式的值保持不变的是( )
A. B. C. D.
【答案】C
11. 如图,中,,,的值为,则( )
A. B. C. D.
【答案】D
12. 在平面直角坐标系中,若点P的横坐标和纵坐标相等,则称点P为完美点.已知二次函数的图象上有且只有一个完美点,且当时,函数的最小值为最大值为1,则m的取值范围是( )
A. B. C. D.
【答案】B
二、填空题(共4小题,满分16分,每小题4分)
13. 已知是方程的解,则__________.
【答案】
14. 已知反比例函数,若时,,则的取值范围__________.
【答案】
15. 如图,在中,,以为边在外作等边,过点作,垂足为,若,,则的长为___________.
【答案】8
16. 如图,在矩形中,点为边上不与、重合的一个动点,过点作交于点,交于点,以为对称轴折叠矩形,点、的对应点分别是、,连接、,若,,当为直角三角形时,的长为___________.
【答案】或
三、解答题(共9小题,满分98分)
17. 贵阳第十九中学八年级学生参加体育中考,现从八年级学生中抽取部分学生进行问卷调查,通过分析整理绘制了如图两幅统计图,请根据两幅统计图中信息回答下列问题:
(1)求参与调查的学生中,参加排球考试的学生人数;
(2)若八年级共有700名学生,请你估计八年级学生中有多少名学生参加篮球考试?
(3)若从参加足球的3名男生和2名女生中随机抽取2名学生,确定为学校足球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.
【答案】(1)6;(2)350;(3)
18. 十九中趣味数学社的同学用10块高度都是1cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点在上,点和分别与木墙的顶端重合.
(1)求证:;
(2)求两堵木墙之间距离.
【答案】(1)见详解;(2)
19. 随着国内新能源汽车的普及,为了适应社会的需求,全国各地都在加快公共充电桩的建设,某省2018年公共充电桩的数量为2万个,2020年公共充电桩的数量为2.88万个.
(1)求2018年至2020年该省公共充电桩数量的年平均增长率;
(2)按照这样的增长速度,预计2021年该省将新增多少万个公共充电桩?
【答案】(1)2018年至2020年该省公共充电桩数量的年平均增长率为20%.(2)预计2021年该省将新增0.576万个公共充电桩.
20. 如图,一次函数的图象与反比例函数(为常数且)的图象交于、两点,点的横坐标为,与轴交于点.
(1)求此反比例函数的表达式;
(2)若点在轴上,且,求点的坐标.
【答案】(1)反比例函数的表达式为;(2)点P(-,0)或(,0).
21. 某条过路上通行车辆限速为50km/h,在离道路70m的点处建一个监测点,道路的段为监测区(如图)在中,已知,.一辆车通过段的时间为10秒,请判断该车是否超速,并说明理由.(参考数据:,,,,,)
【答案】没有超速,理由见解析
22. 如图,的对角线,交于点,,,.
(1)求证:四边形是菱形;
(2)若,,求的长.
【答案】(1)见解析;(2)2
23. 如图,以为直径的经过的中点,于点.
(1)求证:是的切线;
(2)当,时,求图中阴影部分的面积(结果保留根号和).
【答案】(1)见解析;(2)
24. 甲乙两人先后从地出发沿同一直道去地.设乙出发第时,甲、乙离地的距离分别为,,与之间的函数表达式是,与之间的函数表达式是.
(1)乙出发时,甲离地的距离为____________m.
(2)乙出发至甲到达地这段时间内,
①两人何时相距180m?
②两人何时相距最近?最近距离是多少?
【答案】(1)250;(2)①1min或7min;②当乙出发第4min时,两人相距最近,最近距离是90m
25. 在与中,,,,连接,点为的中点,连接,绕着点旋转.
(1)如图1,当点落在的延长线上时,与的数量关系是:__________;
(2)如图2,当旋转到点落在的延长线上时,与是否仍有具有(1)中的数量关系,如果具有,请给予证明;如果没有,请说明理由;
(3)旋转过程中,若当时,直接写出的值.
【答案】(1);(2)具有,证明见解析;(3)14或.
同课章节目录
