人教版数学八年级上册 第十二章第12课时 三角形全等的判定(二)——SAS课件(共21张ppt)
文档属性
| 名称 | 人教版数学八年级上册 第十二章第12课时 三角形全等的判定(二)——SAS课件(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 524.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-21 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
第十二章 全等三角形
第12课时 三角形全等的判定(二)——SAS
目录
01
本课目标
02
课堂导练
1.探索并正确理解“SAS”的判定方法.
2.会用“SAS”判定方法证明两个三角形全等.
3.能灵活运用“SAS”解决相关的实际问题.
4.了解“SSA”不能作为两个三角形全等的条件.
本课目标
知识重点
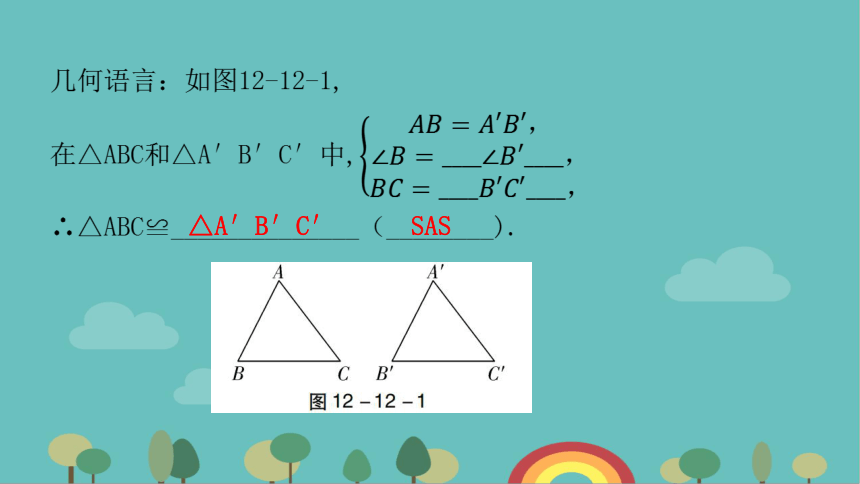
知识点一:三角形全等的判定(SAS)
两边和它们的________分别相等的两个三角形全等(可以简写成“____________”或“________”).
夹角
边角边
SAS
△A′B′C′
SAS
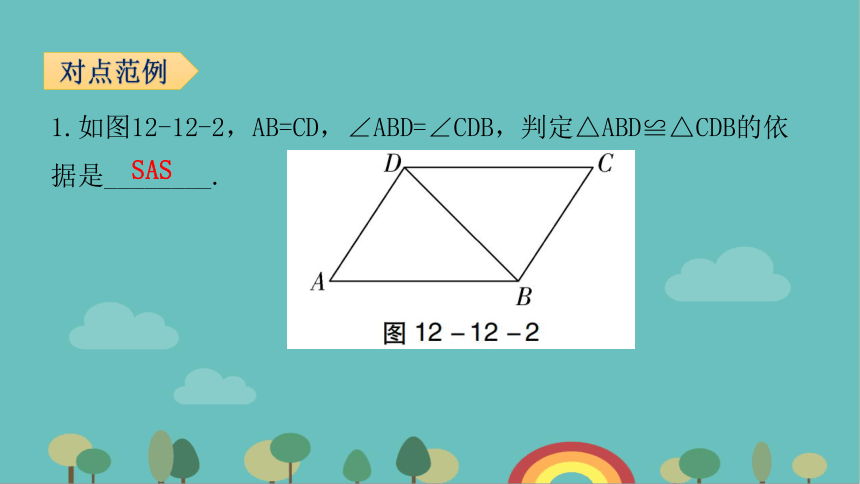
1.如图12-12-2,AB=CD,∠ABD=∠CDB,判定△ABD≌△CDB的依据是________.
对点范例
SAS
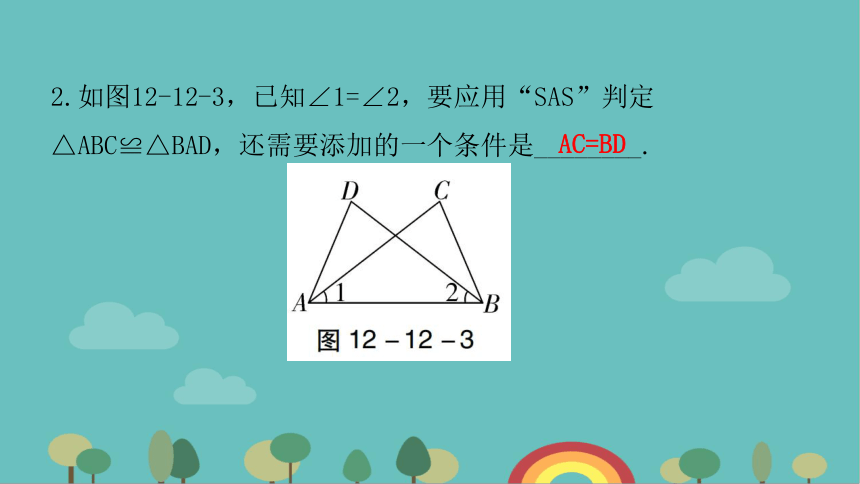
2.如图12-12-3,已知∠1=∠2,要应用“SAS”判定△ABC≌△BAD,还需要添加的一个条件是________.
AC=BD
知识点二:运用“SAS”证明三角形全等
注意:若用“SAS”证明三角形全等,即有两边一角对应相等,其中的“一角”必须是两边的夹角.
知识重点
∠A=∠EDF
AC=DF
AC=DF
SAS
3.如图12-12-5,AB=AE,AC=AD.求证:△ABC≌△AED.
对点范例
课堂导练
【例1】如图12-12-6,已知AB=AD,AC平分∠BAD.△ABC与△ADC全等吗?为什么?
思路点拨:注意隐含条件“公共边是对应边”,利用全等三角形的判定定理“SAS”证明即可.
典型例题
1.(人教八上P44改编)如图12-12-7,点A,D,F,B在同一直线上,AD=BF,AE=BC,且AE∥BC.求证:△AEF≌△BCD.
举一反三
【例2】(人教八上P55改编)如图12-12-8,CA=CD,∠1=∠2,BC=EC.
(1)求证:AB=DE;
(2)当∠B=42°,∠D=29°时,求
∠ECD的度数.
典型例题
(2)解:由(1)知,△ABC≌△DEC,
∴∠E=∠B=42°.
又∵∠D=29°,
∴∠ECD=180°-∠E-∠D=109°.
思路点拨:(1)通过角的和差计算转化为对应角相等,再由“SAS”证明△ABC≌△DEC,可得AB=DE;(2)由全等三角形的性质和三角形的内角和定理可求解.
2.(创新题)如图12-12-9,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD与CE有何位置关系,并证明.
举一反三
(2)解:BD⊥CE,理由如下.
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°.
则∠ABD+∠DBC=45°.
由(1)知,△BAD≌△CAE,
∴∠ABD=∠ACE.
∴∠ACE+∠DBC=45°.
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=45°+45°=90°,即∠BDC=90°.
∴BD⊥CE.
【例3】如图12-12-10,在某公园中有一条“Z”字形绿色长廊ABCD,其中AB∥CD,在AB,BC,CD三段绿色长廊上各修建一凉亭E,M,F,且BE=CF,M是BC的中点,E,M,F在一条直线上.若在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F之间的距离,要测出的长度是( )
A.EM B.BE C.CF D.CM
典型例题
A
3.(人教八上P43改编、北师七下P109改编)如图12-12-11,将两根钢条AA′,BB′的中点O连在一起,使AA′,BB′可以绕着点O自由旋转,就做成了一个测量工件.若测得A′B′=4 cm,则内槽宽AB=________cm.
举一反三
4
谢 谢
第十二章 全等三角形
第12课时 三角形全等的判定(二)——SAS
目录
01
本课目标
02
课堂导练
1.探索并正确理解“SAS”的判定方法.
2.会用“SAS”判定方法证明两个三角形全等.
3.能灵活运用“SAS”解决相关的实际问题.
4.了解“SSA”不能作为两个三角形全等的条件.
本课目标
知识重点
知识点一:三角形全等的判定(SAS)
两边和它们的________分别相等的两个三角形全等(可以简写成“____________”或“________”).
夹角
边角边
SAS
△A′B′C′
SAS
1.如图12-12-2,AB=CD,∠ABD=∠CDB,判定△ABD≌△CDB的依据是________.
对点范例
SAS
2.如图12-12-3,已知∠1=∠2,要应用“SAS”判定△ABC≌△BAD,还需要添加的一个条件是________.
AC=BD
知识点二:运用“SAS”证明三角形全等
注意:若用“SAS”证明三角形全等,即有两边一角对应相等,其中的“一角”必须是两边的夹角.
知识重点
∠A=∠EDF
AC=DF
AC=DF
SAS
3.如图12-12-5,AB=AE,AC=AD.求证:△ABC≌△AED.
对点范例
课堂导练
【例1】如图12-12-6,已知AB=AD,AC平分∠BAD.△ABC与△ADC全等吗?为什么?
思路点拨:注意隐含条件“公共边是对应边”,利用全等三角形的判定定理“SAS”证明即可.
典型例题
1.(人教八上P44改编)如图12-12-7,点A,D,F,B在同一直线上,AD=BF,AE=BC,且AE∥BC.求证:△AEF≌△BCD.
举一反三
【例2】(人教八上P55改编)如图12-12-8,CA=CD,∠1=∠2,BC=EC.
(1)求证:AB=DE;
(2)当∠B=42°,∠D=29°时,求
∠ECD的度数.
典型例题
(2)解:由(1)知,△ABC≌△DEC,
∴∠E=∠B=42°.
又∵∠D=29°,
∴∠ECD=180°-∠E-∠D=109°.
思路点拨:(1)通过角的和差计算转化为对应角相等,再由“SAS”证明△ABC≌△DEC,可得AB=DE;(2)由全等三角形的性质和三角形的内角和定理可求解.
2.(创新题)如图12-12-9,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD与CE有何位置关系,并证明.
举一反三
(2)解:BD⊥CE,理由如下.
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°.
则∠ABD+∠DBC=45°.
由(1)知,△BAD≌△CAE,
∴∠ABD=∠ACE.
∴∠ACE+∠DBC=45°.
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=45°+45°=90°,即∠BDC=90°.
∴BD⊥CE.
【例3】如图12-12-10,在某公园中有一条“Z”字形绿色长廊ABCD,其中AB∥CD,在AB,BC,CD三段绿色长廊上各修建一凉亭E,M,F,且BE=CF,M是BC的中点,E,M,F在一条直线上.若在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F之间的距离,要测出的长度是( )
A.EM B.BE C.CF D.CM
典型例题
A
3.(人教八上P43改编、北师七下P109改编)如图12-12-11,将两根钢条AA′,BB′的中点O连在一起,使AA′,BB′可以绕着点O自由旋转,就做成了一个测量工件.若测得A′B′=4 cm,则内槽宽AB=________cm.
举一反三
4
谢 谢
