14.1轴对称2[上学期]

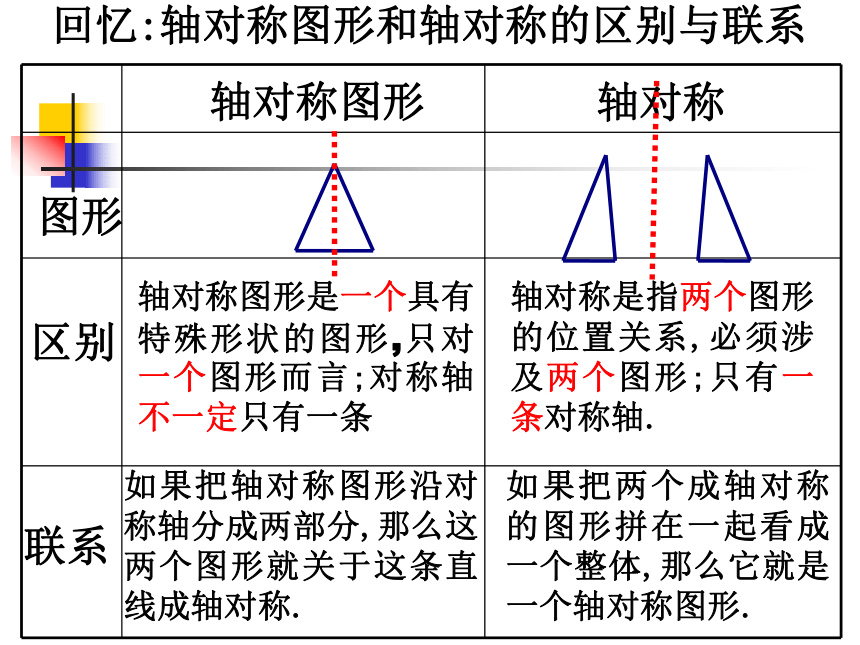
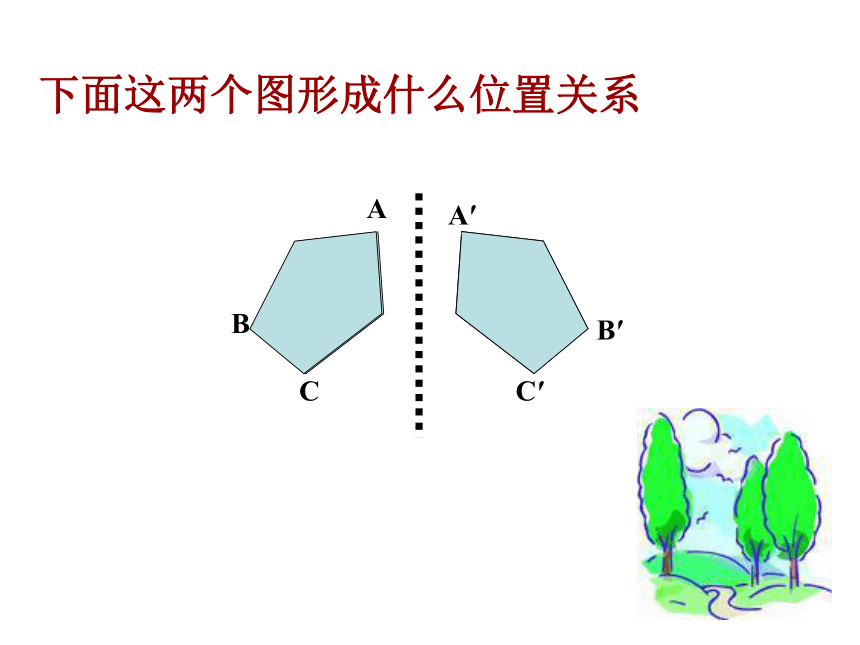
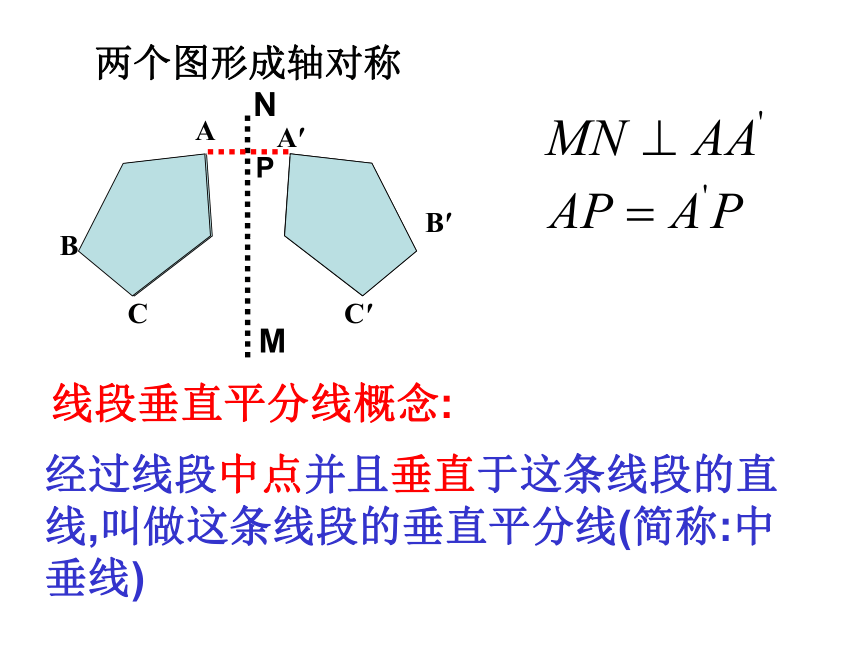
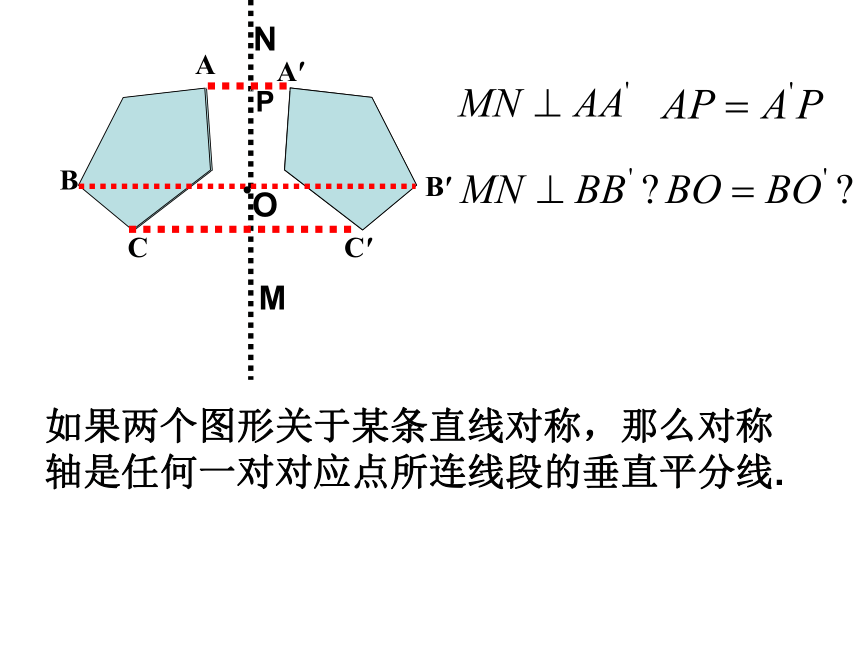
课件29张PPT。14.1轴对称(2)澳门大三巴牌坊回忆:轴对称图形和轴对称的区别与联系 轴对称图形轴对称 区别联系图形 轴对称图形是一个具有特殊形状的图形,只对一个图形而言;对称轴不一定只有一条轴对称是指两个图形的位置关系,必须涉及两个图形;只有一条对称轴.如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线成轴对称.如果把两个成轴对称的图形拼在一起看成一个整体,那么它就是一个轴对称图形. 京剧于清光绪年间形成于北京（一说形成于道光年间）。其前身为徽剧，通称“皮簧戏”同治、光绪两朝，最为盛行 .是中国的一大国粹.曹操张飞窦尔敦A′ABCC′B′下面这两个图形成什么位置关系A′ABCC′B′MNP经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(简称:中垂线)线段垂直平分线概念:两个图形成轴对称A′ABCC′B′MNPO如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线.MNP如果一 个图形是轴对称图形，那么对称轴是任何一对对应点所连线段的垂直平分线图形轴对称的性质:1.如果一 个图形是轴对称图形，那么对称轴是任何一对对应点所连线段的垂直平分线2.如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线.探究线段垂直平分线的性质[探究2]如左图．木条L与AB钉在一起，L垂直平分AB，P1，P2，P3，…是L上的点，分别量一量点P1，P2，P3，…到A与B的距离，你有什么发现？
图2结论：线段垂直平分线上的
点与这条线段两个端点的距离相等 线段垂直平分线的性质1:线段垂直平分线上的点与这条线段两个端点的距离相等线段垂直平分线上的点与这条线段两个端点的距离相等.
你能证明这一结论吗?已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.求证:PA=PB.分析:(1)要证明PA=PB,而△APC≌△BPC的条件由已知 故结论可证.AC=BC,MN⊥AB,可推知其能满足公理（SAS）.就需要证明PA,PB所在的△APC≌△BPC， 性质1:线段垂直平分线上的点与这条线段两个端点的距离相等提示:这个结论是经常用来证明两条线段相等的根据之一.书写应用格式：
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点与这条线段两个端点距离相等).www.czsx.com.cn拓展：如图所示，在△ABC中，AB=AC＝32，MN是AB的垂直平分线，且有BC=21，求△BCN的周长。 如图，△ABC中，AB的垂直平分线分别交AB、BC于点D、E，AC的垂直平分线分别交AC、BC于点F、G，BC=8,则△AEG的周长=______用一根木棒和一根弹性均匀的橡皮筋，做一 个简易的“弓”，“箭”通过木棒中央的孔射出去，怎样才能保持射出去的方向与木棒垂直呢？为什么
CBA只要AB=BC就可以与一条线段两个端点距离相等的点，在这条线段的垂直平分线上ABC 线段垂直平分线的性质2:与线段两个端距离相等的点,在这条线段的垂直平分线上性质2:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.书写格式
∵PA=PB(已知),
∴点P在AB的垂直平分线上(与一条线段两个端点距离相等的点,在这条线段的垂直平分线上).提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.结论:线段垂直平分线上的点 与这条线段两个端点的距离相等。反之，与线段两个端点的距离相等的点在这条线段垂直平分线上。 所以，线段垂直平分线可以看作到线段两端的距离相等的所有点的集合。一起来应用一下吧x2x2x 已知:如图,在ΔABC中, AB、BC的中垂线交于点O，那么点O在AC的中垂线吗？为什么？BAC例题讲解2、如图，AB=AC，MB=MC，直线AM是线段BC的垂直平分线吗？2、如图，AB=AC，MB=MC，直线AM是线段BC的垂直平分线吗？由AB=AC,MB=MC,
可知点A,M都在线段BC的垂直
根据:两点确定一条直线,
直线AM就是显得BC的垂直平分线平分线上,
如图，二(7)班与二(8)班两个班的学生分别在M、N两处参加植树劳动，现要在道路AB、AC的交叉区域内设一个茶水供应点P，使P到两条道路的距离相等，且PM=PN，请你用折纸的方法找出P点并说明理由。?MNBCA做一做 P4.与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.一个概念:垂直并且平分线段的直线叫做这条线段的垂直平分线。简称中垂线。
3.线段垂直平分线上的点与这条线段的两个端点距离相等。 通过今天这节课你有什么收获?感悟与反思：四条性质:1.如果一 个图形是轴对称图形，那么对称轴是任何一对对应点所连线段的垂直平分线2.如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线.再见！