轴对称2[上学期]
图片预览


文档简介
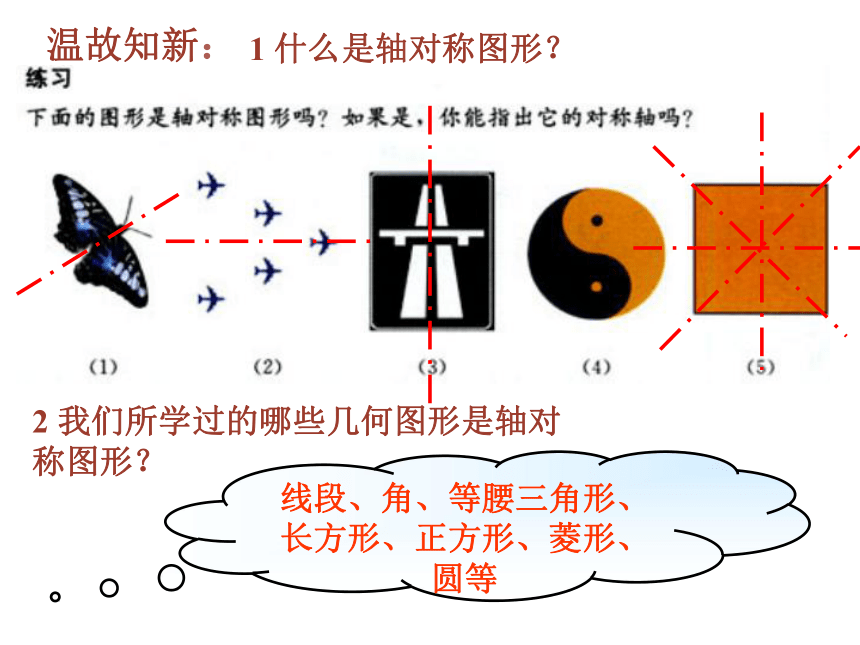
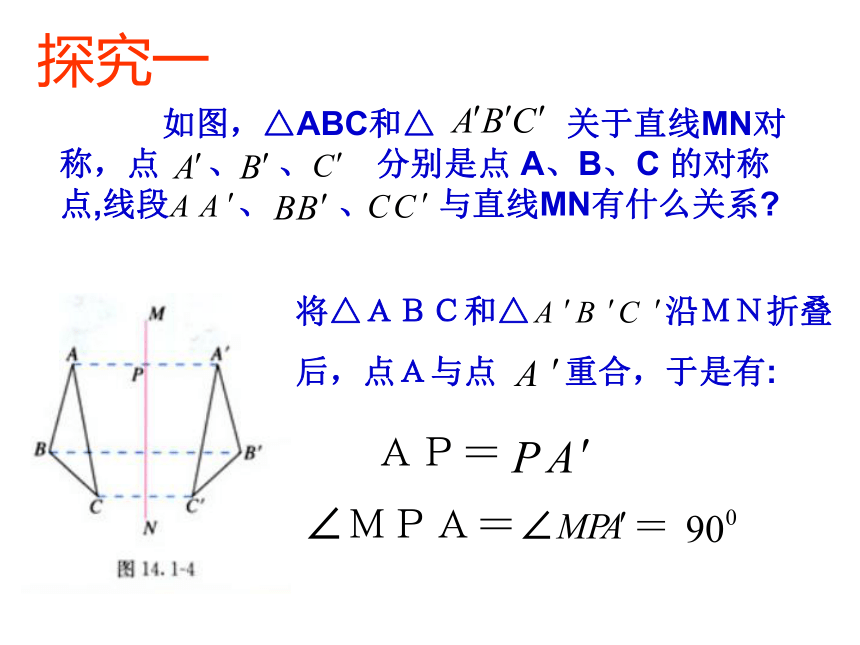
课件24张PPT。 轴 对 称(2) 温故知新:1 什么是轴对称图形?2 我们所学过的哪些几何图形是轴对称图形?线段、角、等腰三角形、长方形、正方形、菱形、圆等 如图,△ABC和△ 关于直线MN对称,点 、 、 分别是点 A、B、C 的对称点,线段 、 、 与直线MN有什么关系? 探究一AP=∠MPA=∠ =将△ABC和△ 沿MN折叠
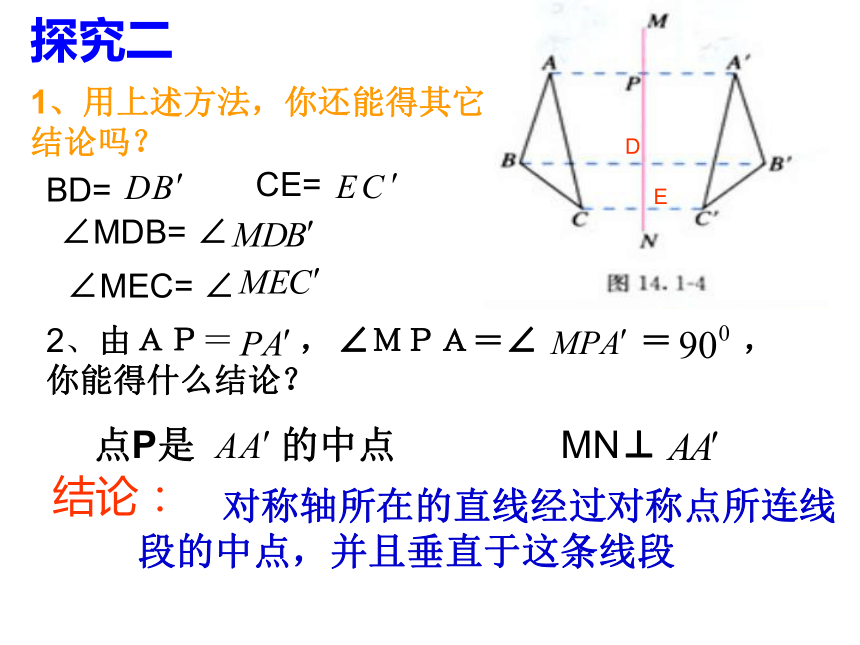
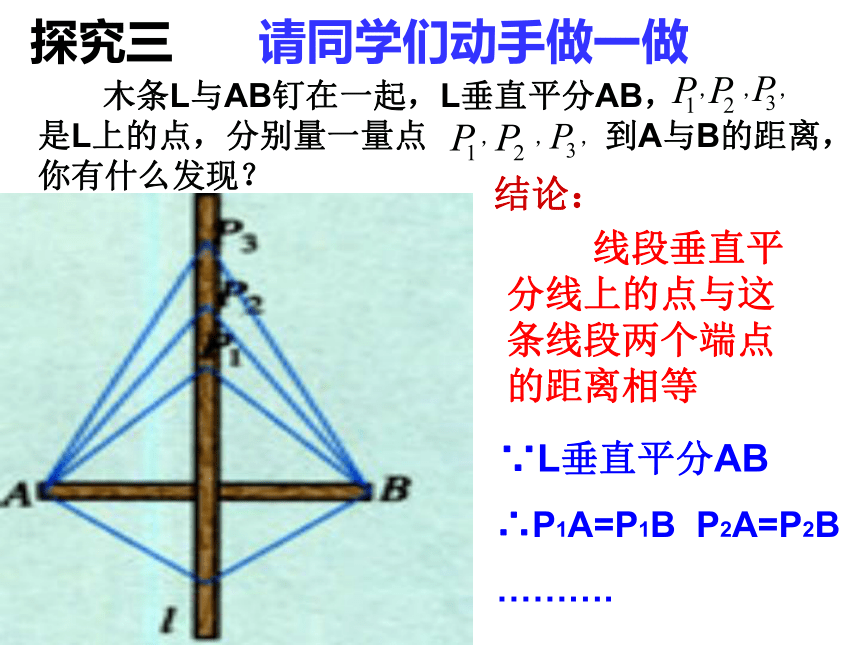
后,点A与点 重合,于是有:探究二1、用上述方法,你还能得其它的结论吗?DEBD= CE= ∠MDB= ∠∠MEC= ∠2、由 , ,你能得什么结论?AP=∠MPA=∠ =点P是 的中点MN⊥ 对称轴所在的直线经过对称点所连线段的中点,并且垂直于这条线段结论:线段的垂直平分线经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线轴对称的性质:1、如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线 2、如果一 个图形是轴对称图形,那么对称轴是任何一对对应点所连线段的垂直平分线L垂直平分L垂直平分L垂直平分探究三 请同学们动手做一做 木条L与AB钉在一起,L垂直平分AB, 是L上的点,分别量一量点 到A与B的距离,你有什么发现? ∵L垂直平分AB∴P1A=P1B P2A=P2B
………. 线段垂直平分线上的点与这条线段两个端点的距离相等结论:线段垂直平分线上的点与这条线段两个端点距离相等.
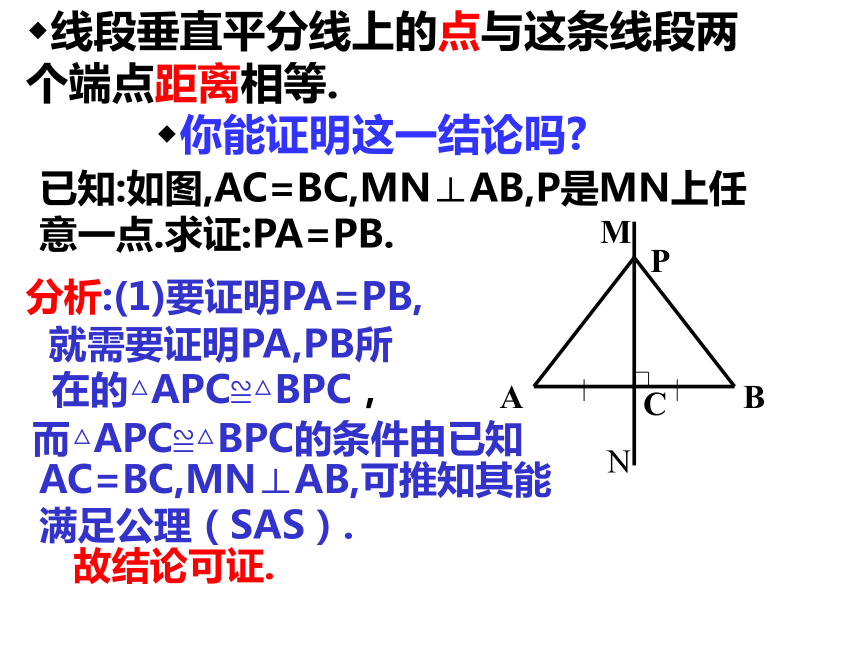
你能证明这一结论吗?已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.求证:PA=PB.分析:(1)要证明PA=PB,而△APC≌△BPC的条件由已知 故结论可证.AC=BC,MN⊥AB,可推知其能满足公理(SAS).就需要证明PA,PB所在的△APC≌△BPC,定理 线段垂直平分线上的点到这条线段两个端点距离相等.
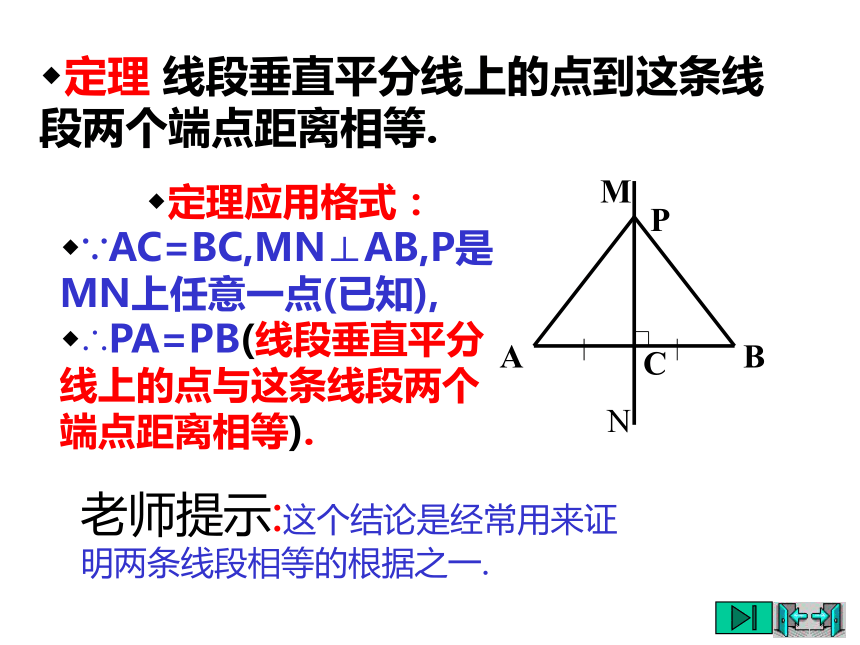
老师提示:这个结论是经常用来证明两条线段相等的根据之一.定理应用格式:
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
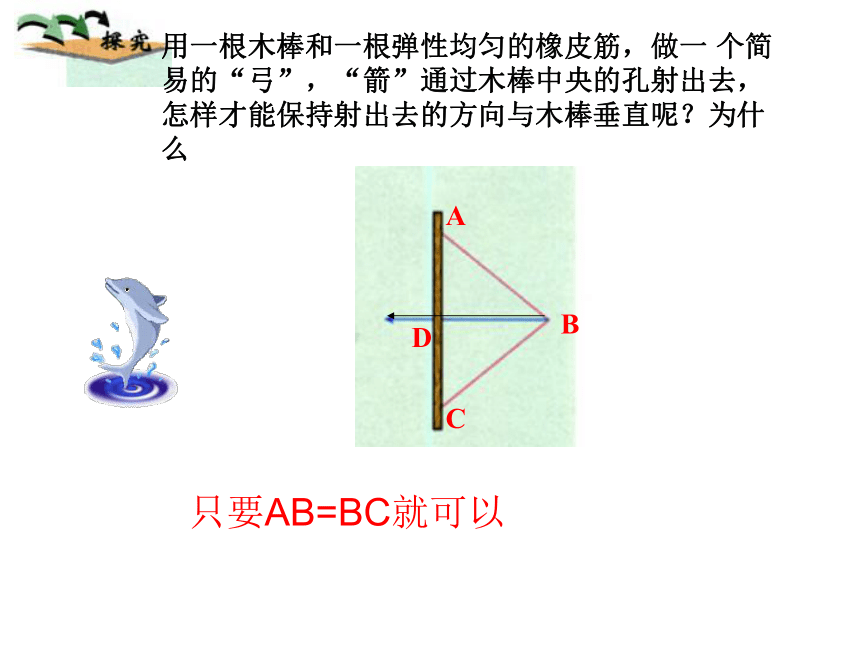
∴PA=PB(线段垂直平分线上的点与这条线段两个端点距离相等).用一根木棒和一根弹性均匀的橡皮筋,做一 个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出去的方向与木棒垂直呢?为什么
CBA只要AB=BC就可以ABCD思考如果PA=PB,怎么证明点P是在线段AB的垂直平分线上呢?ACBPMN 与一条线段两个端点距离相等的点,在这条线段的垂直平分线上结论:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.定理应用格式:
∵PA=PB(已知),
∴点P在AB的垂直平分线上 (与一条线段两个端点距离相等的点,在这条线段的垂直平分线上).老师提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.结论:线段垂直平分线上的点 与这条线段两个端点的距离相等。反之,与线段两个端点的距离相等的点在这条线段垂直平分线上。 所以,线段垂直平分线可以看作到线段两端的距离相等的所有点的集合。练一练 1、 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE 的长度有什么关系?AB+BD 与DE有什么关系?AB=AC=CEAB+BD=DE2、如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?由AB=AC,MB=MC,
可知点A,M都在线段BC的垂直平分线
根据:两点确定一条直线,
直线AM就是显得BC的垂直平分线上,
拓展:如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长。解:∵MN是AB的垂直平分线
∴NA=NB
∴BN+NC=AN+NC=AC
又∵BC=21,AC=32
∴BC+BN+NC=21+32=53
答:△BCN的周长为53.已知: △ABC中,边AB、 BC的垂直平分线交于点P。 求证:PA=PB=PC.结论:三角形三边的垂直平分线交于一点,并且这点到三个顶点的距离相等。(外心) 证明:∵P点在AB的垂直平分线上
∴PA=PB
同理:PB=PC
∴PA=PB=PC 如图,二.3班与二.6班两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且PM=PN,请你用折纸的方法找出P点并说明理由。?MNBCA做一做 PA′ 如图,EFGH是矩形的台球桌面,有两球分别位于A、B两点的位置,试问怎样撞击A球,才能使A球先碰撞台边EF反弹后再击中B球?试一试:解:1.作点A关于EF的对称点A′ 2.连结A′B交EF于点C则沿AC撞击黑球A,必沿CB反弹击中白球B。C试一试:1、一次晚会上,主持人出了一道题目:“如何把 变成一个真正的等式”,很长时间没有人答出,小兰根据这节课的知识很快解决了这道题目,你知道她是怎样做的吗?
我的收获(4)?与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.(1)线段是轴对称图形。 (2)垂直并且平分线段的直线叫做这条线段的垂直平分线。简称中垂线。 (3)线段垂直平分线上的点与这条线段的两个端点距离相等。 通过今天这节课你有什么收获?感悟与反思:下图是由小正方形组成的L形图,请你在图中添画一个小正方形,使它成为轴对称图形,并画出对称轴。四、试一试二、想一想下列图形是由两个基本图形□与 △的.□△△□△△□△△……
请仔细观察规律,并回答问题:
(1)第2003个图案是什么图形?
(2)在图形中,自左往右取4个图案是否成轴对称?还可以有 其他取法,使取出的图案构成轴对称图形吗?有什么规律,才能成轴对称?
后,点A与点 重合,于是有:探究二1、用上述方法,你还能得其它的结论吗?DEBD= CE= ∠MDB= ∠∠MEC= ∠2、由 , ,你能得什么结论?AP=∠MPA=∠ =点P是 的中点MN⊥ 对称轴所在的直线经过对称点所连线段的中点,并且垂直于这条线段结论:线段的垂直平分线经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线轴对称的性质:1、如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线 2、如果一 个图形是轴对称图形,那么对称轴是任何一对对应点所连线段的垂直平分线L垂直平分L垂直平分L垂直平分探究三 请同学们动手做一做 木条L与AB钉在一起,L垂直平分AB, 是L上的点,分别量一量点 到A与B的距离,你有什么发现? ∵L垂直平分AB∴P1A=P1B P2A=P2B
………. 线段垂直平分线上的点与这条线段两个端点的距离相等结论:线段垂直平分线上的点与这条线段两个端点距离相等.
你能证明这一结论吗?已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.求证:PA=PB.分析:(1)要证明PA=PB,而△APC≌△BPC的条件由已知 故结论可证.AC=BC,MN⊥AB,可推知其能满足公理(SAS).就需要证明PA,PB所在的△APC≌△BPC,定理 线段垂直平分线上的点到这条线段两个端点距离相等.
老师提示:这个结论是经常用来证明两条线段相等的根据之一.定理应用格式:
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点与这条线段两个端点距离相等).用一根木棒和一根弹性均匀的橡皮筋,做一 个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出去的方向与木棒垂直呢?为什么
CBA只要AB=BC就可以ABCD思考如果PA=PB,怎么证明点P是在线段AB的垂直平分线上呢?ACBPMN 与一条线段两个端点距离相等的点,在这条线段的垂直平分线上结论:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.定理应用格式:
∵PA=PB(已知),
∴点P在AB的垂直平分线上 (与一条线段两个端点距离相等的点,在这条线段的垂直平分线上).老师提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.结论:线段垂直平分线上的点 与这条线段两个端点的距离相等。反之,与线段两个端点的距离相等的点在这条线段垂直平分线上。 所以,线段垂直平分线可以看作到线段两端的距离相等的所有点的集合。练一练 1、 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE 的长度有什么关系?AB+BD 与DE有什么关系?AB=AC=CEAB+BD=DE2、如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?由AB=AC,MB=MC,
可知点A,M都在线段BC的垂直平分线
根据:两点确定一条直线,
直线AM就是显得BC的垂直平分线上,
拓展:如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长。解:∵MN是AB的垂直平分线
∴NA=NB
∴BN+NC=AN+NC=AC
又∵BC=21,AC=32
∴BC+BN+NC=21+32=53
答:△BCN的周长为53.已知: △ABC中,边AB、 BC的垂直平分线交于点P。 求证:PA=PB=PC.结论:三角形三边的垂直平分线交于一点,并且这点到三个顶点的距离相等。(外心) 证明:∵P点在AB的垂直平分线上
∴PA=PB
同理:PB=PC
∴PA=PB=PC 如图,二.3班与二.6班两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且PM=PN,请你用折纸的方法找出P点并说明理由。?MNBCA做一做 PA′ 如图,EFGH是矩形的台球桌面,有两球分别位于A、B两点的位置,试问怎样撞击A球,才能使A球先碰撞台边EF反弹后再击中B球?试一试:解:1.作点A关于EF的对称点A′ 2.连结A′B交EF于点C则沿AC撞击黑球A,必沿CB反弹击中白球B。C试一试:1、一次晚会上,主持人出了一道题目:“如何把 变成一个真正的等式”,很长时间没有人答出,小兰根据这节课的知识很快解决了这道题目,你知道她是怎样做的吗?
我的收获(4)?与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.(1)线段是轴对称图形。 (2)垂直并且平分线段的直线叫做这条线段的垂直平分线。简称中垂线。 (3)线段垂直平分线上的点与这条线段的两个端点距离相等。 通过今天这节课你有什么收获?感悟与反思:下图是由小正方形组成的L形图,请你在图中添画一个小正方形,使它成为轴对称图形,并画出对称轴。四、试一试二、想一想下列图形是由两个基本图形□与 △的.□△△□△△□△△……
请仔细观察规律,并回答问题:
(1)第2003个图案是什么图形?
(2)在图形中,自左往右取4个图案是否成轴对称?还可以有 其他取法,使取出的图案构成轴对称图形吗?有什么规律,才能成轴对称?
