14-1 轴对称(3)[上学期]
文档属性
| 名称 | 14-1 轴对称(3)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-06 00:00:00 | ||
图片预览


文档简介
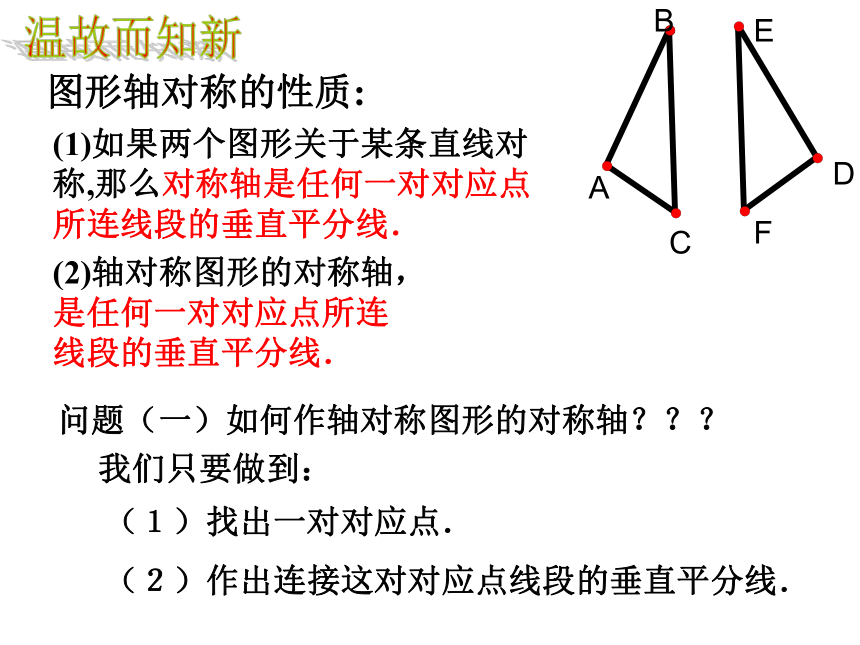
课件10张PPT。14.1 轴对称(3)图形轴对称的性质:(1)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线. (2)轴对称图形的对称轴,是任何一对对应点所连
线段的垂直平分线. 温故而知新问题(一)如何作轴对称图形的对称轴???我们只要做到:(1)找出一对对应点.(2)作出连接这对对应点线段的垂直平分线.问题(二)如何作出线段的垂直平分线.(经过线段中点并且垂直于这条线段的直线)根据线段的垂直平分线的定义:
(1)找出线段中点.
(2)过中点作这条线段的垂线.如何用尺规作图法作出线段的垂直平分线??思考:提示:由两点确定一条直线和
线段的垂直平分线的性质,只要作出到
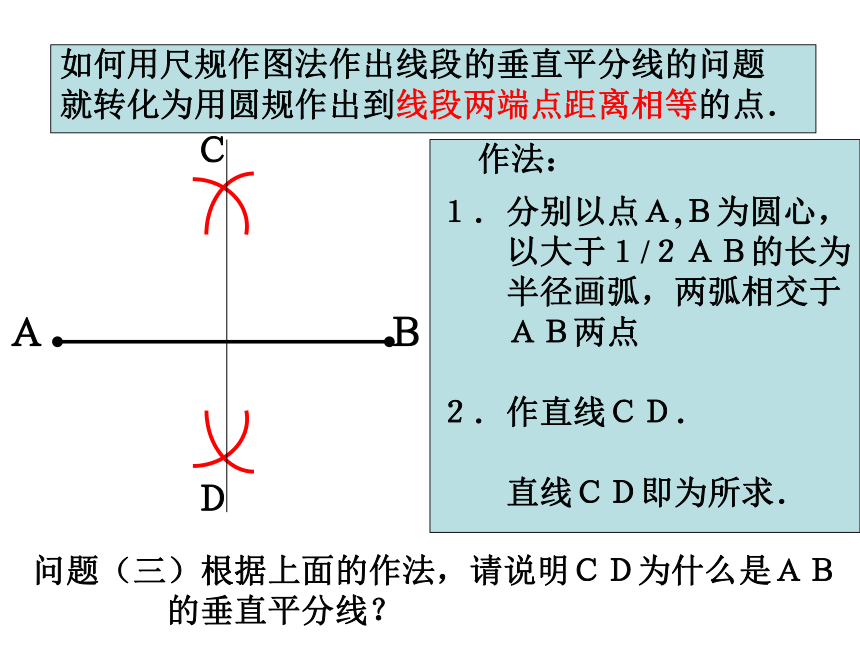
线段两端点距离相等的两个点即可.如何用尺规作图法作出线段的垂直平分线的问题
就转化为用圆规作出到线段两端点距离相等的点.作法:1.分别以点A,B为圆心,
以大于1/2AB的长为
半径画弧,两弧相交于
AB两点
2.作直线CD.
直线CD即为所求.AB问题(三)根据上面的作法,请说明CD为什么是AB
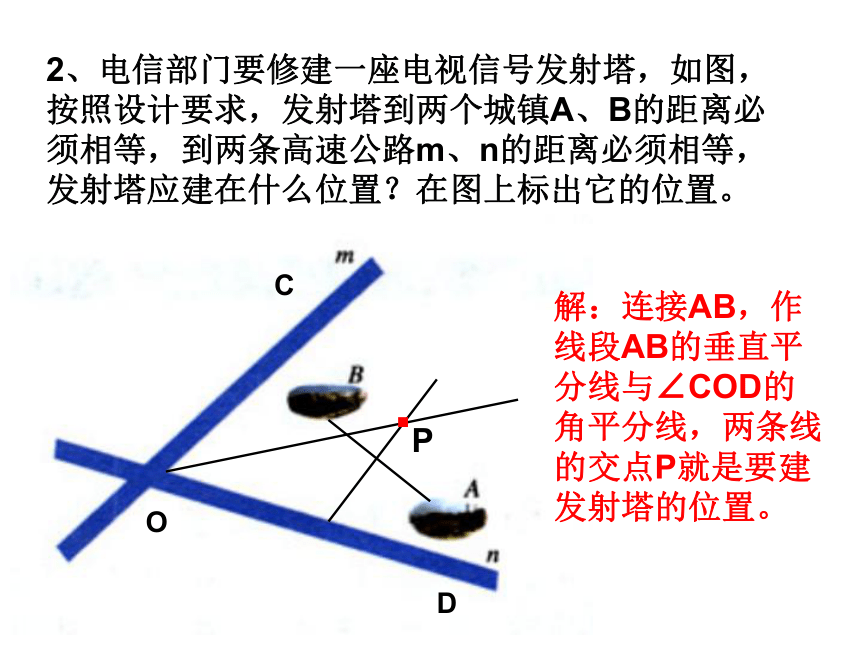
的垂直平分线? 2、电信部门要修建一座电视信号发射塔,如图,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条高速公路m、n的距离必须相等,发射塔应建在什么位置?在图上标出它的位置。P解:连接AB,作线段AB的垂直平分线与∠COD的角平分线,两条线的交点P就是要建发射塔的位置。COD.ABCA′B′C′P△ABC与△A′B′C′关于某条直线对称,请你作出它的对称轴。MN就是它们的对称轴。下图中的五角星是轴对称图形吗?若是,有几条对称轴?
你能作出这些对称轴吗?AA1A2作法:1.找出五角星的一对对应点
A、A1 , 连接AA12.作出线段AA1的垂直平分线 点评:只要找到任意一组对应点,作出这对对应点连线的垂直平分线,就可以得到此图形的对称轴. [例4]有时我们感觉两个图形是轴对称,如何验证。
如图,△ABC与△DEF关于某条直线成轴对称吗?归纳:如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称。
用这种方法可以判定两个图形是否关于某条直线对称。5、如图,AD是△ABC的角平分线,DE、DF分别
是△ABD和△ACD的高。
求证:AD垂直平分EF。6、如图是由两个等边三角形组成的图形,它是轴对称
图形吗?若不是,请移动一个三角形,使它与另一
个三角形组成轴对称图形。怎样移动,才能使所构
成的图形具有可能多的对称轴? 如图甲,△ABC和△A′B′C′关于直线L对称,延长对应线
段AC和A′C′,两条延长线相交吗?交点与对称轴L有什么
关系?延长其他对应线段呢?在图乙中,AC与A′C′又如何
呢?再找几个成轴对称的图形观察一下,能发现什么规律吗? 结论:成轴对称的两个图形,对应线段的延长线如果相
交,交点一定在对称轴上;对应线段的延长线如
果不相交,也就是对应线段所在的直线平行,那
么它们也与对称轴平行.
线段的垂直平分线. 温故而知新问题(一)如何作轴对称图形的对称轴???我们只要做到:(1)找出一对对应点.(2)作出连接这对对应点线段的垂直平分线.问题(二)如何作出线段的垂直平分线.(经过线段中点并且垂直于这条线段的直线)根据线段的垂直平分线的定义:
(1)找出线段中点.
(2)过中点作这条线段的垂线.如何用尺规作图法作出线段的垂直平分线??思考:提示:由两点确定一条直线和
线段的垂直平分线的性质,只要作出到
线段两端点距离相等的两个点即可.如何用尺规作图法作出线段的垂直平分线的问题
就转化为用圆规作出到线段两端点距离相等的点.作法:1.分别以点A,B为圆心,
以大于1/2AB的长为
半径画弧,两弧相交于
AB两点
2.作直线CD.
直线CD即为所求.AB问题(三)根据上面的作法,请说明CD为什么是AB
的垂直平分线? 2、电信部门要修建一座电视信号发射塔,如图,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条高速公路m、n的距离必须相等,发射塔应建在什么位置?在图上标出它的位置。P解:连接AB,作线段AB的垂直平分线与∠COD的角平分线,两条线的交点P就是要建发射塔的位置。COD.ABCA′B′C′P△ABC与△A′B′C′关于某条直线对称,请你作出它的对称轴。MN就是它们的对称轴。下图中的五角星是轴对称图形吗?若是,有几条对称轴?
你能作出这些对称轴吗?AA1A2作法:1.找出五角星的一对对应点
A、A1 , 连接AA12.作出线段AA1的垂直平分线 点评:只要找到任意一组对应点,作出这对对应点连线的垂直平分线,就可以得到此图形的对称轴. [例4]有时我们感觉两个图形是轴对称,如何验证。
如图,△ABC与△DEF关于某条直线成轴对称吗?归纳:如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称。
用这种方法可以判定两个图形是否关于某条直线对称。5、如图,AD是△ABC的角平分线,DE、DF分别
是△ABD和△ACD的高。
求证:AD垂直平分EF。6、如图是由两个等边三角形组成的图形,它是轴对称
图形吗?若不是,请移动一个三角形,使它与另一
个三角形组成轴对称图形。怎样移动,才能使所构
成的图形具有可能多的对称轴? 如图甲,△ABC和△A′B′C′关于直线L对称,延长对应线
段AC和A′C′,两条延长线相交吗?交点与对称轴L有什么
关系?延长其他对应线段呢?在图乙中,AC与A′C′又如何
呢?再找几个成轴对称的图形观察一下,能发现什么规律吗? 结论:成轴对称的两个图形,对应线段的延长线如果相
交,交点一定在对称轴上;对应线段的延长线如
果不相交,也就是对应线段所在的直线平行,那
么它们也与对称轴平行.
