北师大版八年级数学下册试题 第三章 《图形的平移与旋转》单元测试卷(含答案)
文档属性
| 名称 | 北师大版八年级数学下册试题 第三章 《图形的平移与旋转》单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 739.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 10:35:28 | ||
图片预览


文档简介
第三章 《图形的平移与旋转》单元测试卷
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.对称美是美的一种重要形式,它能给与人们一种圆满、协调和平的美感,常被运用于建筑、器物、绘画、标识等作品的设计上,下列汽车的标识是中心对称图形的是( )
A. B.
C. D.
2.如图,正方形网格中的每个小正方形的边长为1,将绕旋转中心旋转后得到△,其中点,,的对应点分别是点,、,那么旋转中心是( )
A.点 B.点 C.点 D.点
3.如图,人民公园内一块长方形草地上原有一条宽的笔直小路,现要将这条小路改造成弯曲小路,小路的上边线向下平移就是它的下边线,那么改造后小路的面积( )
A.变大了 B.变小了 C.没变 D.无法确定
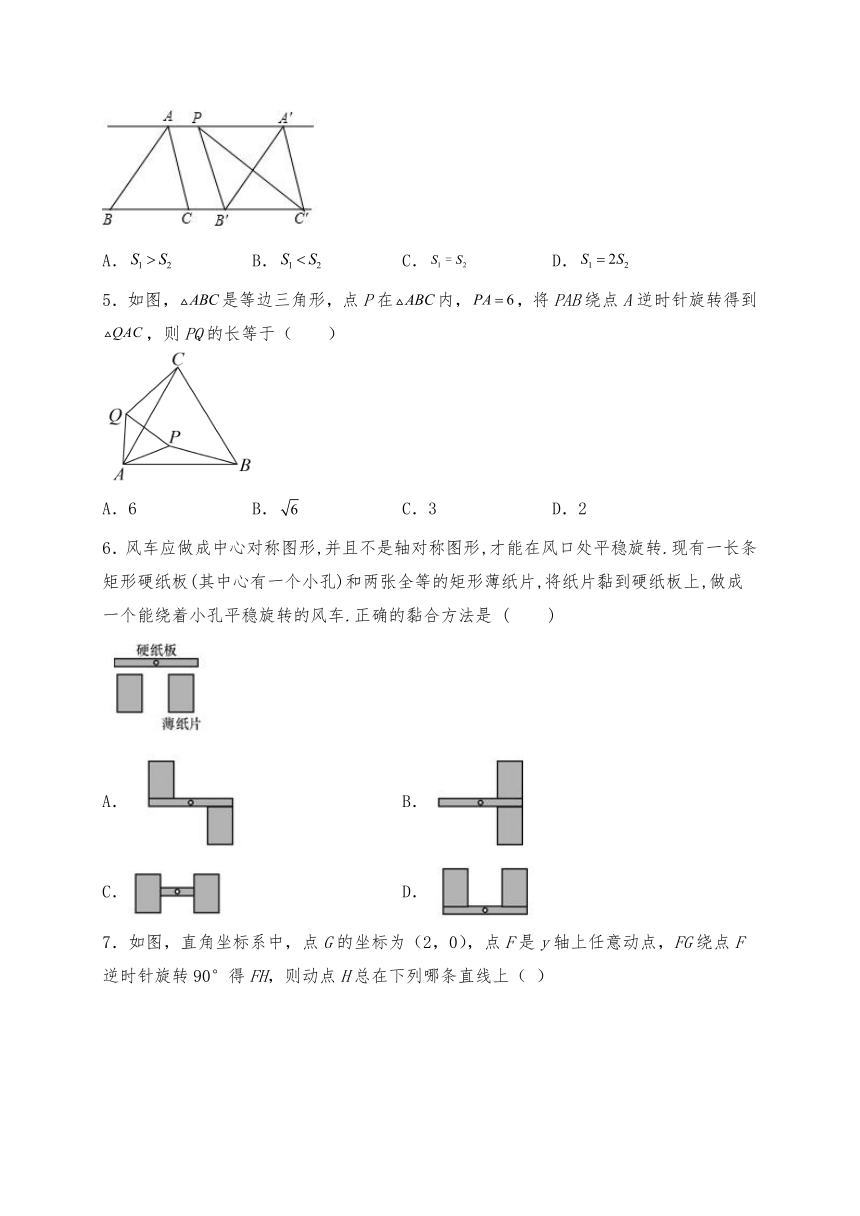
4.如图,△ABC沿着BC方向平移得到△A′B′C′,点P是直线AA′上任意一点,若△ABC、△PB′C′的面积分别为,则下列关系正确的是( )
A. B. C. D.
5.如图,是等边三角形,点P在内,,将PAB绕点A逆时针旋转得到,则PQ的长等于( )
A.6 B. C.3 D.2
6.风车应做成中心对称图形,并且不是轴对称图形,才能在风口处平稳旋转.现有一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片,将纸片黏到硬纸板上,做成一个能绕着小孔平稳旋转的风车.正确的黏合方法是 ( )
A. B.
C. D.
7.如图,直角坐标系中,点G的坐标为(2,0),点F是y轴上任意动点,FG绕点F逆时针旋转90°得FH,则动点H总在下列哪条直线上( )
A. B. C. D.
8.图1是正方体的平面展开图,六个面的点数分别为1、2、3、4、5、6,将点数朝外折叠成一枚正方体骰子,并放置于水平桌面上,如图2所示,若骰子初始位置为图2所示的状态,将骰子向右翻滚,则完成1次翻转,此时骰子朝下一面的点数是2,那么按上述规则连续完成2次翻折后,骰子朝下一面的点数是3;则连续完成2020次翻折后,骰子朝下一面的点数是( )
A.2 B.3 C.4 D.5
9.如图,将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD,连接CD.若AB=4cm.则△BCD的面积为( )
A.4 B.2 C.3 D.2
10.如图,在平面直角坐标系xOy中,⊙P的半径为2,点P的坐标为(﹣3,0),若将⊙P沿x轴向右平移,使得点(0,1)落在⊙P上,则⊙P向右平移的距离为( )
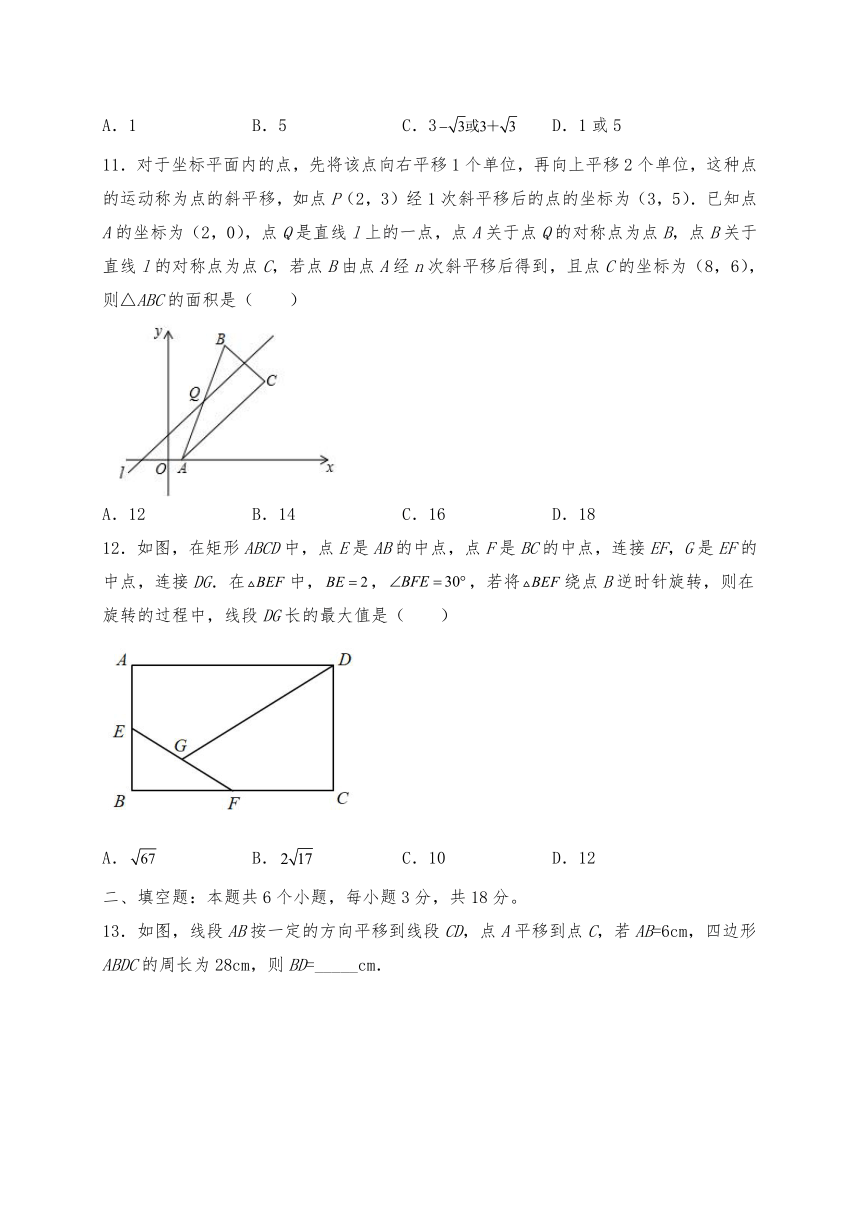
A.1 B.5 C.3 D.1或5
11.对于坐标平面内的点,先将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5).已知点A的坐标为(2,0),点Q是直线l上的一点,点A关于点Q的对称点为点B,点B关于直线l的对称点为点C,若点B由点A经n次斜平移后得到,且点C的坐标为(8,6),则△ABC的面积是( )
A.12 B.14 C.16 D.18
12.如图,在矩形ABCD中,点E是AB的中点,点F是BC的中点,连接EF,G是EF的中点,连接DG.在中,,,若将绕点B逆时针旋转,则在旋转的过程中,线段DG长的最大值是( )
A. B. C.10 D.12
二、填空题:本题共6个小题,每小题3分,共18分。
13.如图,线段AB按一定的方向平移到线段CD,点A平移到点C,若AB=6cm,四边形ABDC的周长为28cm,则BD=_____cm.
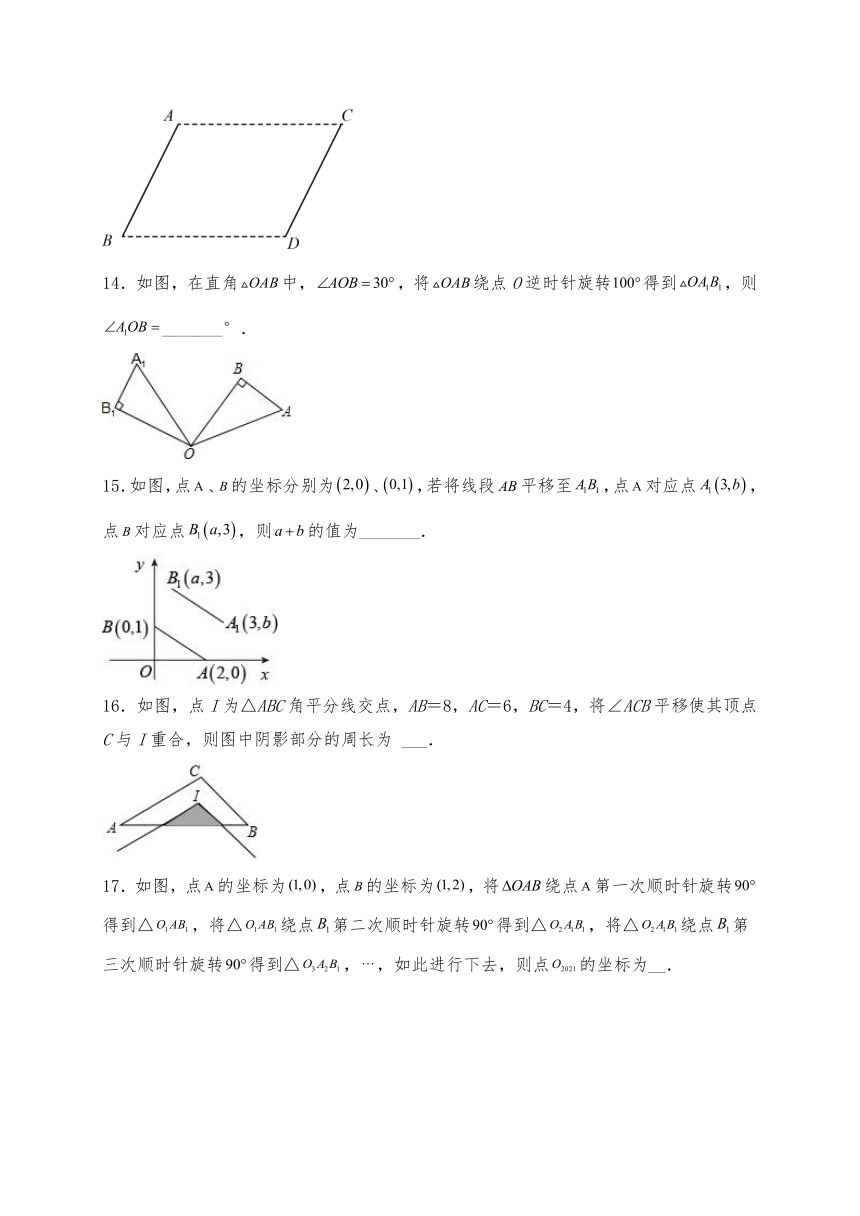
14.如图,在直角中,,将绕点O逆时针旋转得到,则_______°.
15.如图,点、的坐标分别为、,若将线段平移至,点对应点,点对应点,则的值为_______.
16.如图,点I为△ABC角平分线交点,AB=8,AC=6,BC=4,将∠ACB平移使其顶点C与I重合,则图中阴影部分的周长为 ___.
17.如图,点的坐标为,点的坐标为,将绕点第一次顺时针旋转得到△,将△绕点第二次顺时针旋转得到△,将△绕点第三次顺时针旋转得到△,,如此进行下去,则点的坐标为__.
18.在直角△ABC中,∠C=90°,∠B=30°,AC=6,点D是CB边上的动点,连接AD,将线段AD顺时针旋转60°,得到线段AP,连接CP,线段CP的最小值是______.
三、解答题(19题6分,其余每题8分,共46分)
19.如图,在中,,,将边CB绕点C顺时针旋转60,得到线段CD,连接AD,BD.
(1)根据题意,将图形补充完整;
(2)求的度数.
20.南湖公园有很多的长方形草地,草地里修了很多有趣的小路,下面三个图形都是长为50米,宽为30米的长方形草地,且小路的宽都是1米.
①如图1,阴影部分为1米宽的小路,长方形除去阴影部分后剩余部分为草地,则草地的面积为 ;
②如图2,有两条宽均为1米的小路(图中阴影部分),求草地的面积.
③如图3,非阴影部分为1米宽的小路,沿着小路的中间从入口E处走到出口F处,所走的路线(图中虚线)长为 .
21.已知∠AOB=160°,∠COE是直角,OF平分∠AOE.
(1)如图1,若∠COF=32°,则∠BOE= ;
(2)如图1,若∠COF=m°,则∠BOE= ;∠BOE与∠COF的数量关系为 ;
(3)在已知条件不变的前提下,当∠COE绕点O逆时针转动到如图2的位置时,第(2)问中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
22.如图1,在平面直角坐标系中,点A(a,2),B(b,4),且a,b满足关系式(a+5)2+=0
(1)直接写出A,B两点的坐标:A( , ),B( , );
(2)线段AB以每秒2个单位长度的速度向右水平移动,A,B的对应点分别为A1,B1;(友情提示:S△ABO表示三角形ABO的面积)
①如图2,若线段A1B1交y轴于点C,当时,求平移时间t的值;
②若直线A1B1交y轴于点C,当时,试求出平移时间t的值,并直接写出点C的坐标.
23.已知:在Rt△ABC中,,,,左右作平行移动的等边三角形的两个顶点、始终在边上,、分别与相交于点、.
(1)如图1,当点与点重合时,点恰好在斜边上,求的周长;
(2)如图2,在作平行移动的过程中,图中是否存在与线段始终相等的线段?如果存在,请指出这条线段,并加以证明;如果不存在,请说明理由;
(3)假设点与点的距离为,与的重叠部分的面积为,求与的函数关系式,并写出定义域.
24.如图1,点的坐标为,点为轴正半轴上一个动点,将点绕着点顺时针旋转90°到的位置.
(1)若点的横坐标为:-2,求直线的函数表达式;
(2)如图2,若轴恰好平分,与轴相交于点,过点作于点,试探究与的数量关系;
(3)如图3,将点绕着点逆时针旋转90°到点,连接,在点的运动过程中,与轴相交于点,则线段的长度是否改变?若不变,求出的长度,若改变,请说明理由.
答案
一、选择题。
C.C.C.C.A.A.A.C.C.C.A.C.
二、填空题。
13.8.
14.70.
15.3.
16.
17..
18.3.
三、解答题
19.
(1)
补充图形如下:
(2)
根据画图,可知,,
∴是等边三角形,
∴.
∵,,
∴,,
∴,
∴.
20.
①将小路往左平移,直到E、F与A、B重合,
则平移后的四边形是一个矩形,并且,,
则草地的面积为:(平方米);
②将小路往AB、AD边平移,直到小路与草地的边重合,
则草地的面积为:(平方米);
③将小路往AB、AD、DC边平移,直到小路与草地的边重合,
则所走的路线(图中虚线)长为:(米).
21.(1)
解:∵∠COE是直角,∠COF=32°,
∴ ,
∵OF平分∠AOE,
∴ ,
∵∠AOB=160°,
∴ ;
(2)
当∠COF=m°,
∴ ,
∴ ,
∴ ,
∴ ;
(3)
∠BOE与∠COF的数量关系仍然成立,
设 ,
∵∠COE是直角,
∴ ,
∵OF平分∠AOE,
∴ ,
∴ ,
即∠BOE=2∠COF-20°
22.解:(1),
,,
,,
,,
故答案为:,;
(2)线段以每秒2个单位长度的速度向右水平移动,
平移秒后,,,
①如图2,作轴于,轴于,
,
,
即,
整理得:,
解得;
②,
即,
解得,
此时,,,,
,
即,
,
解得,
点的坐标为.
23.(1)
解:在中,,,,
,,
是等边三角形,
,
,
,
,
的周长;
(2)
解:结论:.
理由:,,
,
是等边三角形,
,
,
,
,
,
;
(3)
,
,
.
24.(1)
解:如图1,
作CH⊥BO于H,则CH=2,
∵∠CBH+∠ABO=90°,∠ABO+∠BAO=90°,
∴∠CBH=∠BAO,
在△ABO和△BCH中,
,
∴△ABO≌△BCH(AAS),
∴BO=CH=2,
∴B点坐标(0,2),
设直线AB表达式为:y=kx+b,
把A(4,0),B(0,2)代入,得,
解得:,
故直线AB表达式为:y=kx+2;
(2)解:AE=2CD,
如图②,
延长AB,CD交于点N,
∵,
∴∠ADN=∠ADC=90°,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ADN和△ADC中,,
∴△ADN≌△ADC(ASA),
∴CD=ND,
∴CN=2CD,
∵∠N+∠BAD=90°,∠N+∠BCN=90°,
∴∠BAD=∠BCN,
在△ABE和△CBN中,,
∴△ABE≌△CBN(ASA),
∴AE=CN,
∴AE=2CD;
(3)解:故线段BF的长度不变,为2,理由如下:
∵点A的坐标为,
∴OA=4,
如图3,作CG⊥BO于G,
∵∠CBG+∠ABO=90°,∠ABO+∠BAO=90°,
∴∠CBG=∠BAO,
在△ABO和△BCG中,
,
∴△ABO≌△BCG(AAS),
∴OA = BG =4,BO=CG,
由旋转可知:BO=BD,∠OBD=90 ,
∴BD=CG,
在△DBF和△CGF中,
,
∴△DBF≌△CGF(AAS),
∴BF =GF,
∴BF =BG=2.
故线段BF的长度不变,为2.
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.对称美是美的一种重要形式,它能给与人们一种圆满、协调和平的美感,常被运用于建筑、器物、绘画、标识等作品的设计上,下列汽车的标识是中心对称图形的是( )
A. B.
C. D.
2.如图,正方形网格中的每个小正方形的边长为1,将绕旋转中心旋转后得到△,其中点,,的对应点分别是点,、,那么旋转中心是( )
A.点 B.点 C.点 D.点
3.如图,人民公园内一块长方形草地上原有一条宽的笔直小路,现要将这条小路改造成弯曲小路,小路的上边线向下平移就是它的下边线,那么改造后小路的面积( )
A.变大了 B.变小了 C.没变 D.无法确定
4.如图,△ABC沿着BC方向平移得到△A′B′C′,点P是直线AA′上任意一点,若△ABC、△PB′C′的面积分别为,则下列关系正确的是( )
A. B. C. D.
5.如图,是等边三角形,点P在内,,将PAB绕点A逆时针旋转得到,则PQ的长等于( )
A.6 B. C.3 D.2
6.风车应做成中心对称图形,并且不是轴对称图形,才能在风口处平稳旋转.现有一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片,将纸片黏到硬纸板上,做成一个能绕着小孔平稳旋转的风车.正确的黏合方法是 ( )
A. B.
C. D.
7.如图,直角坐标系中,点G的坐标为(2,0),点F是y轴上任意动点,FG绕点F逆时针旋转90°得FH,则动点H总在下列哪条直线上( )
A. B. C. D.
8.图1是正方体的平面展开图,六个面的点数分别为1、2、3、4、5、6,将点数朝外折叠成一枚正方体骰子,并放置于水平桌面上,如图2所示,若骰子初始位置为图2所示的状态,将骰子向右翻滚,则完成1次翻转,此时骰子朝下一面的点数是2,那么按上述规则连续完成2次翻折后,骰子朝下一面的点数是3;则连续完成2020次翻折后,骰子朝下一面的点数是( )
A.2 B.3 C.4 D.5
9.如图,将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD,连接CD.若AB=4cm.则△BCD的面积为( )
A.4 B.2 C.3 D.2
10.如图,在平面直角坐标系xOy中,⊙P的半径为2,点P的坐标为(﹣3,0),若将⊙P沿x轴向右平移,使得点(0,1)落在⊙P上,则⊙P向右平移的距离为( )
A.1 B.5 C.3 D.1或5
11.对于坐标平面内的点,先将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5).已知点A的坐标为(2,0),点Q是直线l上的一点,点A关于点Q的对称点为点B,点B关于直线l的对称点为点C,若点B由点A经n次斜平移后得到,且点C的坐标为(8,6),则△ABC的面积是( )
A.12 B.14 C.16 D.18
12.如图,在矩形ABCD中,点E是AB的中点,点F是BC的中点,连接EF,G是EF的中点,连接DG.在中,,,若将绕点B逆时针旋转,则在旋转的过程中,线段DG长的最大值是( )
A. B. C.10 D.12
二、填空题:本题共6个小题,每小题3分,共18分。
13.如图,线段AB按一定的方向平移到线段CD,点A平移到点C,若AB=6cm,四边形ABDC的周长为28cm,则BD=_____cm.
14.如图,在直角中,,将绕点O逆时针旋转得到,则_______°.
15.如图,点、的坐标分别为、,若将线段平移至,点对应点,点对应点,则的值为_______.
16.如图,点I为△ABC角平分线交点,AB=8,AC=6,BC=4,将∠ACB平移使其顶点C与I重合,则图中阴影部分的周长为 ___.
17.如图,点的坐标为,点的坐标为,将绕点第一次顺时针旋转得到△,将△绕点第二次顺时针旋转得到△,将△绕点第三次顺时针旋转得到△,,如此进行下去,则点的坐标为__.
18.在直角△ABC中,∠C=90°,∠B=30°,AC=6,点D是CB边上的动点,连接AD,将线段AD顺时针旋转60°,得到线段AP,连接CP,线段CP的最小值是______.
三、解答题(19题6分,其余每题8分,共46分)
19.如图,在中,,,将边CB绕点C顺时针旋转60,得到线段CD,连接AD,BD.
(1)根据题意,将图形补充完整;
(2)求的度数.
20.南湖公园有很多的长方形草地,草地里修了很多有趣的小路,下面三个图形都是长为50米,宽为30米的长方形草地,且小路的宽都是1米.
①如图1,阴影部分为1米宽的小路,长方形除去阴影部分后剩余部分为草地,则草地的面积为 ;
②如图2,有两条宽均为1米的小路(图中阴影部分),求草地的面积.
③如图3,非阴影部分为1米宽的小路,沿着小路的中间从入口E处走到出口F处,所走的路线(图中虚线)长为 .
21.已知∠AOB=160°,∠COE是直角,OF平分∠AOE.
(1)如图1,若∠COF=32°,则∠BOE= ;
(2)如图1,若∠COF=m°,则∠BOE= ;∠BOE与∠COF的数量关系为 ;
(3)在已知条件不变的前提下,当∠COE绕点O逆时针转动到如图2的位置时,第(2)问中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
22.如图1,在平面直角坐标系中,点A(a,2),B(b,4),且a,b满足关系式(a+5)2+=0
(1)直接写出A,B两点的坐标:A( , ),B( , );
(2)线段AB以每秒2个单位长度的速度向右水平移动,A,B的对应点分别为A1,B1;(友情提示:S△ABO表示三角形ABO的面积)
①如图2,若线段A1B1交y轴于点C,当时,求平移时间t的值;
②若直线A1B1交y轴于点C,当时,试求出平移时间t的值,并直接写出点C的坐标.
23.已知:在Rt△ABC中,,,,左右作平行移动的等边三角形的两个顶点、始终在边上,、分别与相交于点、.
(1)如图1,当点与点重合时,点恰好在斜边上,求的周长;
(2)如图2,在作平行移动的过程中,图中是否存在与线段始终相等的线段?如果存在,请指出这条线段,并加以证明;如果不存在,请说明理由;
(3)假设点与点的距离为,与的重叠部分的面积为,求与的函数关系式,并写出定义域.
24.如图1,点的坐标为,点为轴正半轴上一个动点,将点绕着点顺时针旋转90°到的位置.
(1)若点的横坐标为:-2,求直线的函数表达式;
(2)如图2,若轴恰好平分,与轴相交于点,过点作于点,试探究与的数量关系;
(3)如图3,将点绕着点逆时针旋转90°到点,连接,在点的运动过程中,与轴相交于点,则线段的长度是否改变?若不变,求出的长度,若改变,请说明理由.
答案
一、选择题。
C.C.C.C.A.A.A.C.C.C.A.C.
二、填空题。
13.8.
14.70.
15.3.
16.
17..
18.3.
三、解答题
19.
(1)
补充图形如下:
(2)
根据画图,可知,,
∴是等边三角形,
∴.
∵,,
∴,,
∴,
∴.
20.
①将小路往左平移,直到E、F与A、B重合,
则平移后的四边形是一个矩形,并且,,
则草地的面积为:(平方米);
②将小路往AB、AD边平移,直到小路与草地的边重合,
则草地的面积为:(平方米);
③将小路往AB、AD、DC边平移,直到小路与草地的边重合,
则所走的路线(图中虚线)长为:(米).
21.(1)
解:∵∠COE是直角,∠COF=32°,
∴ ,
∵OF平分∠AOE,
∴ ,
∵∠AOB=160°,
∴ ;
(2)
当∠COF=m°,
∴ ,
∴ ,
∴ ,
∴ ;
(3)
∠BOE与∠COF的数量关系仍然成立,
设 ,
∵∠COE是直角,
∴ ,
∵OF平分∠AOE,
∴ ,
∴ ,
即∠BOE=2∠COF-20°
22.解:(1),
,,
,,
,,
故答案为:,;
(2)线段以每秒2个单位长度的速度向右水平移动,
平移秒后,,,
①如图2,作轴于,轴于,
,
,
即,
整理得:,
解得;
②,
即,
解得,
此时,,,,
,
即,
,
解得,
点的坐标为.
23.(1)
解:在中,,,,
,,
是等边三角形,
,
,
,
,
的周长;
(2)
解:结论:.
理由:,,
,
是等边三角形,
,
,
,
,
,
;
(3)
,
,
.
24.(1)
解:如图1,
作CH⊥BO于H,则CH=2,
∵∠CBH+∠ABO=90°,∠ABO+∠BAO=90°,
∴∠CBH=∠BAO,
在△ABO和△BCH中,
,
∴△ABO≌△BCH(AAS),
∴BO=CH=2,
∴B点坐标(0,2),
设直线AB表达式为:y=kx+b,
把A(4,0),B(0,2)代入,得,
解得:,
故直线AB表达式为:y=kx+2;
(2)解:AE=2CD,
如图②,
延长AB,CD交于点N,
∵,
∴∠ADN=∠ADC=90°,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ADN和△ADC中,,
∴△ADN≌△ADC(ASA),
∴CD=ND,
∴CN=2CD,
∵∠N+∠BAD=90°,∠N+∠BCN=90°,
∴∠BAD=∠BCN,
在△ABE和△CBN中,,
∴△ABE≌△CBN(ASA),
∴AE=CN,
∴AE=2CD;
(3)解:故线段BF的长度不变,为2,理由如下:
∵点A的坐标为,
∴OA=4,
如图3,作CG⊥BO于G,
∵∠CBG+∠ABO=90°,∠ABO+∠BAO=90°,
∴∠CBG=∠BAO,
在△ABO和△BCG中,
,
∴△ABO≌△BCG(AAS),
∴OA = BG =4,BO=CG,
由旋转可知:BO=BD,∠OBD=90 ,
∴BD=CG,
在△DBF和△CGF中,
,
∴△DBF≌△CGF(AAS),
∴BF =GF,
∴BF =BG=2.
故线段BF的长度不变,为2.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
