北师大版八年级数学下册试题 第三章《图形的平移与旋转》复习卷(含答案)
文档属性
| 名称 | 北师大版八年级数学下册试题 第三章《图形的平移与旋转》复习卷(含答案) | 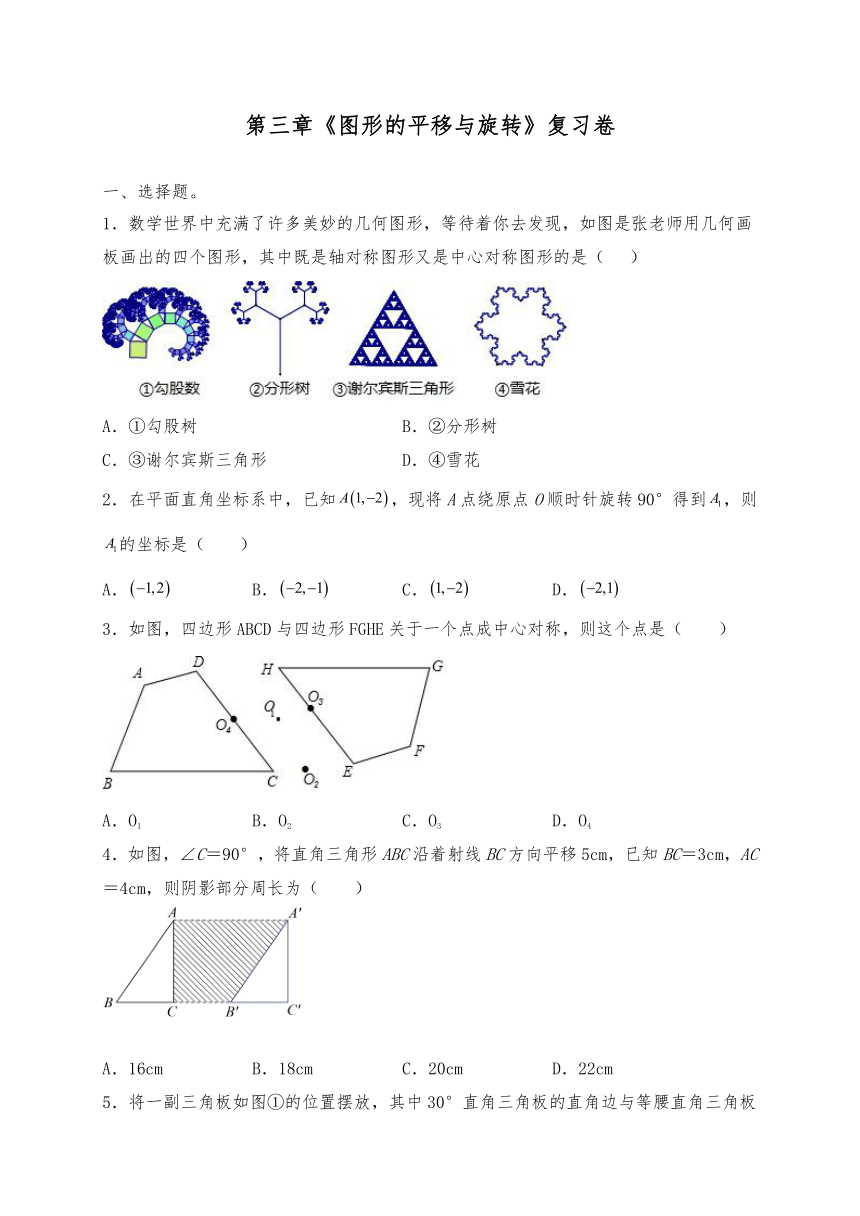 | |
| 格式 | zip | ||
| 文件大小 | 273.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 10:35:58 | ||
图片预览



文档简介
第三章《图形的平移与旋转》复习卷
一、选择题。
1.数学世界中充满了许多美妙的几何图形,等待着你去发现,如图是张老师用几何画板画出的四个图形,其中既是轴对称图形又是中心对称图形的是( )
A.①勾股树 B.②分形树
C.③谢尔宾斯三角形 D.④雪花
2.在平面直角坐标系中,已知,现将A点绕原点O顺时针旋转90°得到,则的坐标是( )
A. B. C. D.
3.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是( )
A.O1 B.O2 C.O3 D.O4
4.如图,∠C=90°,将直角三角形ABC沿着射线BC方向平移5cm,已知BC=3cm,AC=4cm,则阴影部分周长为( )
A.16cm B.18cm C.20cm D.22cm
5.将一副三角板如图①的位置摆放,其中30°直角三角板的直角边与等腰直角三角板的斜边重合,30°直角三角板直角顶点与等腰直角三角板的锐角顶点重合(为点O).现将30°的直角三角板绕点O顺时针旋转至如图②的位置,此时,则( )
A.30° B.25° C.20° D.15°
6.边长为2的两种正方形卡片如上图①所示,卡片中的扇形半径均为2,图②是交替摆放A、B两种卡片得到的图案.若摆放这个图案共用两种卡片2021张,则这个图案中阴影部分图形的面积和为( )
A.4040 B.4044–π C.4044 D.4044+π
7.已知:O为直线AB上一点,一个三角板COD的直角顶点放在点O上,OE平分∠AOC,OF平分∠BOD,当三角形COD绕O点旋转到如图所示时,对于下列结论:①∠AOD﹣∠EOC=90°;②∠AOC﹣∠BOD=90°;③∠AOE﹣∠BOF=45°;④∠EOF=135°.其中正确的是( )
A.②③④ B.①②③ C.①③④ D.①②④
8.如图,已知点K为直线l:y=2x+4上一点,先将点K向下平移2个单位,再向左平移a个单位至点K1,然后再将点K1向上平移b个单位,向右平1个单位至点K2,若点K2也恰好落在直线l上,则a,b应满足的关系是( )
A.a+2b=4 B.2a﹣b=4 C.2a+b=4 D.a+b=4
二、填空题。
9.在平面直角坐标系中,点M(﹣2,4)关于原点对称的点的坐标是 ___.
10.如图,将边长为5cm的等边△ABC向右平移1cm,得到△A′B′C′,此时阴影部分的周长为_____cm.
11.如图,在平面直角坐标系中,动点P从原点O出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得到点;接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点,…,按此作法进行下去,则点的坐标为_____.
12.如图所示,在中,,将绕点顺时针旋转60°得到,与交于点,则_____°,直线与所夹锐角的度数为_____.
三、解答题。
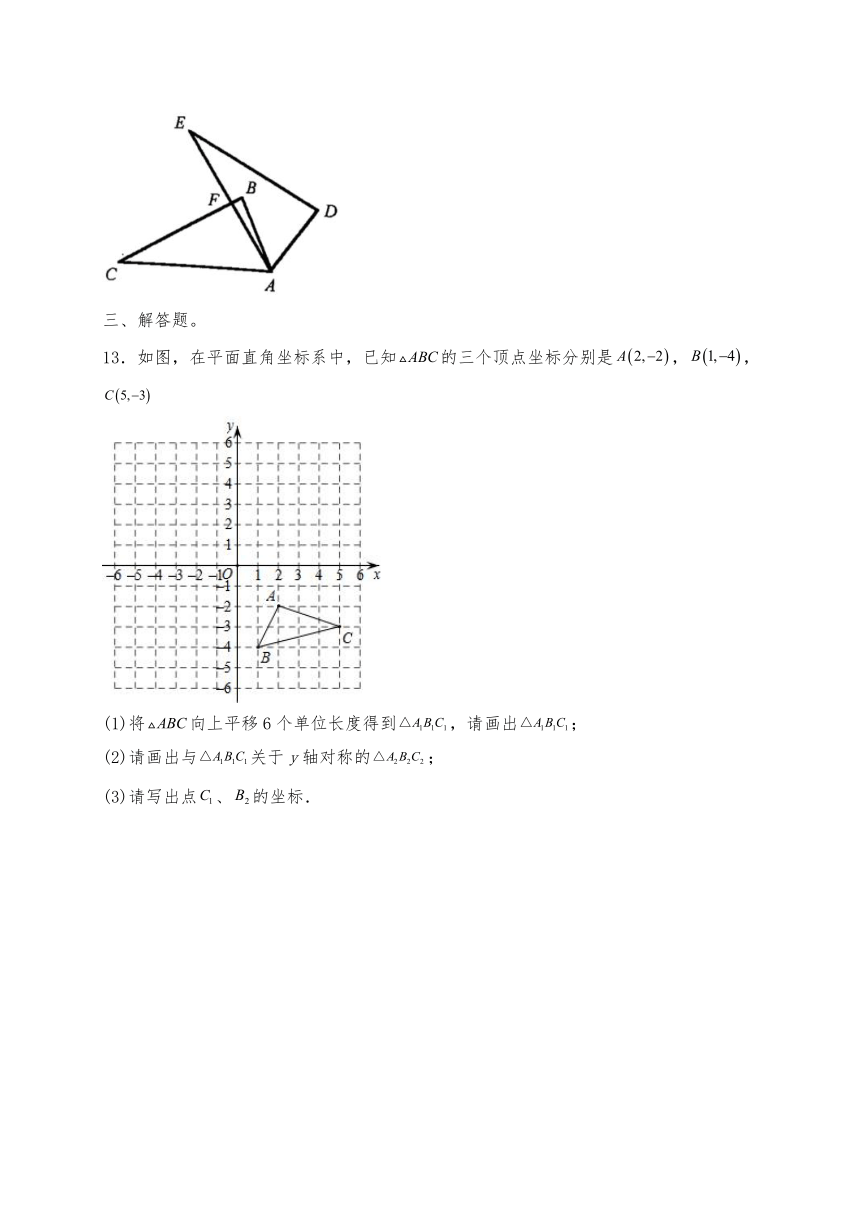
13.如图,在平面直角坐标系中,已知的三个顶点坐标分别是,,
(1)将向上平移6个单位长度得到,请画出;
(2)请画出与关于y轴对称的;
(3)请写出点、的坐标.
14.△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点O顺时针旋转90°得到△A2B2C2;
(2)按照(1)中②作图,回答下列问题:△A2B2C2中顶点A2坐标为 ,C2坐标为 ,若P(a,b)为△ABC边上一点,则点P对应的点P2的坐标为 .
15.(1)如图1,△ABC和△AMN都是等腰直角三角形,直角顶点为点A,△ABC固定不动,△AMN可以绕着点A旋转.
①如图2,将△AMN绕点A旋转,使点M落在BC边上,连接CN.
直接写出图中的全等三角形: ;直接写出线段CN,CM,CB之间满足的等量关系为: ;
②如图2,试探索线段MA,MB,MC之间满足的等量关系,并完整地证明你的结论;
(2)如图3,P是等腰直角△ABC内一点,∠BAC=90°,连接PA,PB,PC,将△BAP绕点A顺时针旋转90°后得到△CAQ,连接PQ.已知PA=2,PB=3,若∠PQC=90°,求PC的长.
答案
一、选择题。
D.B.A.A.B.B.A.C
二、填空题。
9.(2,﹣4).
10.12.
11.(1011,1011)
12. 90 60°
三、解答题。
13.(1)
如图所示:△A1B1C1为所作的图形
(2)如图所示:△A2B2C2,为所作的图形
(3)C1(5,3),B2(-1,2)
14.(1)
解:①如图,△A1B1C1即为所求.
②如图,△A2B2C2即为所求.
(2)
解:点A2坐标为(4,2),C2坐标为(1,3),若P(a,b)为△ABC边上一点,则点P对应的点P2的坐标为(b,-a).
故答案为:(4,2),(1,3),(b,-a).
15.
解:(1)①∵△ABC和△AMN都是等腰直角三角形,
∴AB=AC,AM=AN
∠BAM+∠MAC=90°,∠CAN+∠MAC=90°,
∴∠BAM=∠CAN,
在△BAM和△CAN中:
BA=CA,∠BAM=∠CAN,AM=AN
∴△BAM≌△CAN(SAS),
∴BM=CN,
∵BM+CM=CB,
∴CN+CM=CB,
故答案为:△BAM≌△CAN,CN+CM=CB;
②MB2+MC2=2MA2;证明如下:
∵△ABC和△AMN都是等腰直角三角形,
∴∠B=∠ACB= 45°=∠AMN=∠ANM
同理①可证△BAM≌△CAN,
∴∠ACN=∠B=45°,
即∠BCN=90°,
∴CN2+MC2=MN2,
在R△MAN中,MN2=MA2+AN2=2MA2,
∴MB2+MC2=2MA2;
(2)由旋转知△BAP≌△CAQ,
∴PA=QA=2,∠PAQ=∠BAC=90°,CQ=BP=3,
∴△PAQ为等腰直角三角形,
∴PQ2=PA2+QA2=22+22=8,
∵∠PQC=90°,
∴PC2=PQ2+QC2=8+32=17,
∴PC=.
一、选择题。
1.数学世界中充满了许多美妙的几何图形,等待着你去发现,如图是张老师用几何画板画出的四个图形,其中既是轴对称图形又是中心对称图形的是( )
A.①勾股树 B.②分形树
C.③谢尔宾斯三角形 D.④雪花
2.在平面直角坐标系中,已知,现将A点绕原点O顺时针旋转90°得到,则的坐标是( )
A. B. C. D.
3.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是( )
A.O1 B.O2 C.O3 D.O4
4.如图,∠C=90°,将直角三角形ABC沿着射线BC方向平移5cm,已知BC=3cm,AC=4cm,则阴影部分周长为( )
A.16cm B.18cm C.20cm D.22cm
5.将一副三角板如图①的位置摆放,其中30°直角三角板的直角边与等腰直角三角板的斜边重合,30°直角三角板直角顶点与等腰直角三角板的锐角顶点重合(为点O).现将30°的直角三角板绕点O顺时针旋转至如图②的位置,此时,则( )
A.30° B.25° C.20° D.15°
6.边长为2的两种正方形卡片如上图①所示,卡片中的扇形半径均为2,图②是交替摆放A、B两种卡片得到的图案.若摆放这个图案共用两种卡片2021张,则这个图案中阴影部分图形的面积和为( )
A.4040 B.4044–π C.4044 D.4044+π
7.已知:O为直线AB上一点,一个三角板COD的直角顶点放在点O上,OE平分∠AOC,OF平分∠BOD,当三角形COD绕O点旋转到如图所示时,对于下列结论:①∠AOD﹣∠EOC=90°;②∠AOC﹣∠BOD=90°;③∠AOE﹣∠BOF=45°;④∠EOF=135°.其中正确的是( )
A.②③④ B.①②③ C.①③④ D.①②④
8.如图,已知点K为直线l:y=2x+4上一点,先将点K向下平移2个单位,再向左平移a个单位至点K1,然后再将点K1向上平移b个单位,向右平1个单位至点K2,若点K2也恰好落在直线l上,则a,b应满足的关系是( )
A.a+2b=4 B.2a﹣b=4 C.2a+b=4 D.a+b=4
二、填空题。
9.在平面直角坐标系中,点M(﹣2,4)关于原点对称的点的坐标是 ___.
10.如图,将边长为5cm的等边△ABC向右平移1cm,得到△A′B′C′,此时阴影部分的周长为_____cm.
11.如图,在平面直角坐标系中,动点P从原点O出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得到点;接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点,…,按此作法进行下去,则点的坐标为_____.
12.如图所示,在中,,将绕点顺时针旋转60°得到,与交于点,则_____°,直线与所夹锐角的度数为_____.
三、解答题。
13.如图,在平面直角坐标系中,已知的三个顶点坐标分别是,,
(1)将向上平移6个单位长度得到,请画出;
(2)请画出与关于y轴对称的;
(3)请写出点、的坐标.
14.△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点O顺时针旋转90°得到△A2B2C2;
(2)按照(1)中②作图,回答下列问题:△A2B2C2中顶点A2坐标为 ,C2坐标为 ,若P(a,b)为△ABC边上一点,则点P对应的点P2的坐标为 .
15.(1)如图1,△ABC和△AMN都是等腰直角三角形,直角顶点为点A,△ABC固定不动,△AMN可以绕着点A旋转.
①如图2,将△AMN绕点A旋转,使点M落在BC边上,连接CN.
直接写出图中的全等三角形: ;直接写出线段CN,CM,CB之间满足的等量关系为: ;
②如图2,试探索线段MA,MB,MC之间满足的等量关系,并完整地证明你的结论;
(2)如图3,P是等腰直角△ABC内一点,∠BAC=90°,连接PA,PB,PC,将△BAP绕点A顺时针旋转90°后得到△CAQ,连接PQ.已知PA=2,PB=3,若∠PQC=90°,求PC的长.
答案
一、选择题。
D.B.A.A.B.B.A.C
二、填空题。
9.(2,﹣4).
10.12.
11.(1011,1011)
12. 90 60°
三、解答题。
13.(1)
如图所示:△A1B1C1为所作的图形
(2)如图所示:△A2B2C2,为所作的图形
(3)C1(5,3),B2(-1,2)
14.(1)
解:①如图,△A1B1C1即为所求.
②如图,△A2B2C2即为所求.
(2)
解:点A2坐标为(4,2),C2坐标为(1,3),若P(a,b)为△ABC边上一点,则点P对应的点P2的坐标为(b,-a).
故答案为:(4,2),(1,3),(b,-a).
15.
解:(1)①∵△ABC和△AMN都是等腰直角三角形,
∴AB=AC,AM=AN
∠BAM+∠MAC=90°,∠CAN+∠MAC=90°,
∴∠BAM=∠CAN,
在△BAM和△CAN中:
BA=CA,∠BAM=∠CAN,AM=AN
∴△BAM≌△CAN(SAS),
∴BM=CN,
∵BM+CM=CB,
∴CN+CM=CB,
故答案为:△BAM≌△CAN,CN+CM=CB;
②MB2+MC2=2MA2;证明如下:
∵△ABC和△AMN都是等腰直角三角形,
∴∠B=∠ACB= 45°=∠AMN=∠ANM
同理①可证△BAM≌△CAN,
∴∠ACN=∠B=45°,
即∠BCN=90°,
∴CN2+MC2=MN2,
在R△MAN中,MN2=MA2+AN2=2MA2,
∴MB2+MC2=2MA2;
(2)由旋转知△BAP≌△CAQ,
∴PA=QA=2,∠PAQ=∠BAC=90°,CQ=BP=3,
∴△PAQ为等腰直角三角形,
∴PQ2=PA2+QA2=22+22=8,
∵∠PQC=90°,
∴PC2=PQ2+QC2=8+32=17,
∴PC=.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
