北师大版七年级数学下册试题 第四章 《三角形》复习卷 (含答案)
文档属性
| 名称 | 北师大版七年级数学下册试题 第四章 《三角形》复习卷 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 335.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 10:42:09 | ||
图片预览

文档简介
第四章 《三角形》复习卷
一、选择题。
1.在下列各组图形中,是全等的图形是( )
A. B.
C. D.
2.已知,图中的虚线部分是小玉作的辅助线,则下列结论正确的是( )
A.CD是边AB上的高 B.CD是边AC上的高
C.BD是边CB上的高 D.BD是边AC上的高
3.如图,△ABC≌△ADE,∠DAC=90°,∠BAE=140°,BC、DE相交于点F,则∠DAB的大小为( )
A.15° B.20° C.25° D.30°
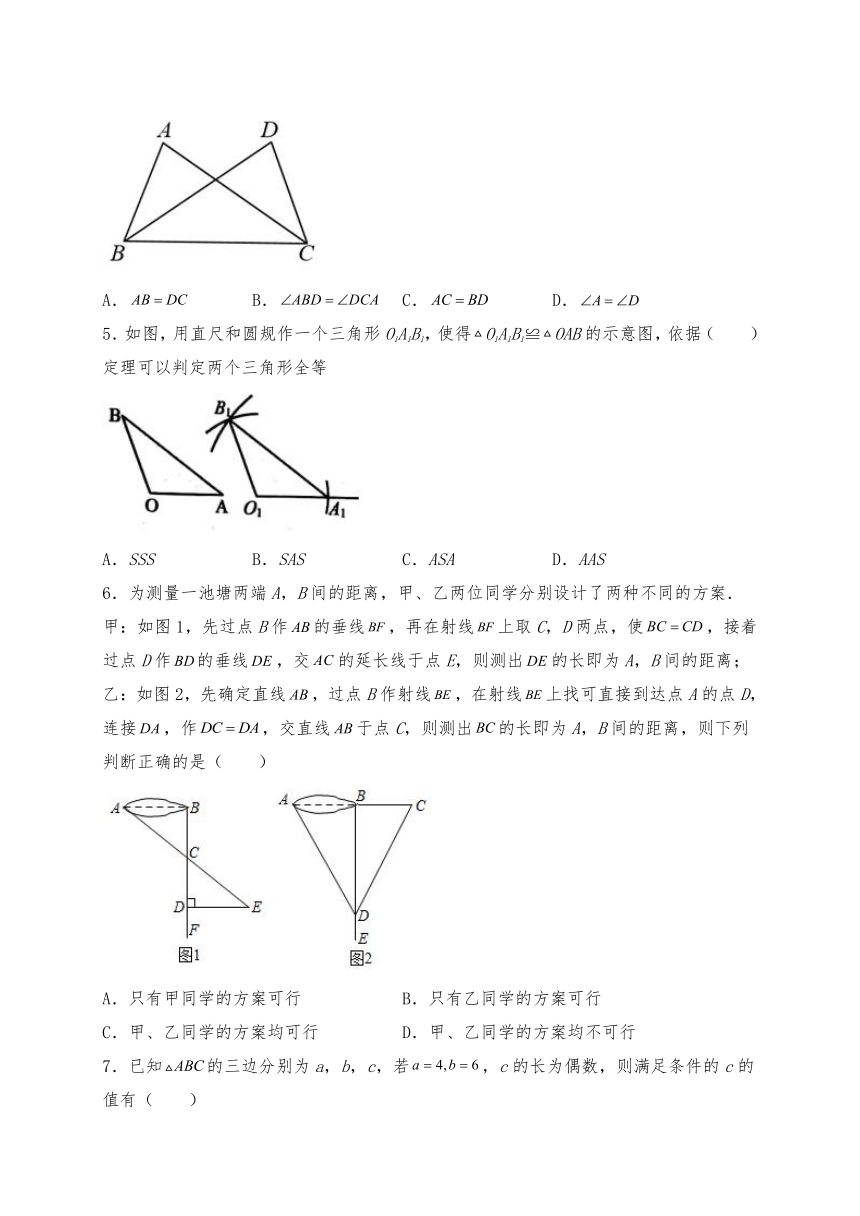
4.在△ABC和△DCB中,,添加一个条件,不能证明△ABC和△DCB全等的是( )
A. B. C. D.
5.如图,用直尺和圆规作一个三角形O1A1B1,使得O1A1B1≌OAB的示意图,依据( )定理可以判定两个三角形全等
A.SSS B.SAS C.ASA D.AAS
6.为测量一池塘两端A,B间的距离,甲、乙两位同学分别设计了两种不同的方案.
甲:如图1,先过点B作的垂线,再在射线上取C,D两点,使,接着过点D作的垂线,交的延长线于点E,则测出的长即为A,B间的距离;
乙:如图2,先确定直线,过点B作射线,在射线上找可直接到达点A的点D,连接,作,交直线于点C,则测出的长即为A,B间的距离,则下列判断正确的是( )
A.只有甲同学的方案可行 B.只有乙同学的方案可行
C.甲、乙同学的方案均可行 D.甲、乙同学的方案均不可行
7.已知的三边分别为a,b,c,若,c的长为偶数,则满足条件的c的值有( )
A.1个 B.2个 C.3个 D.5个
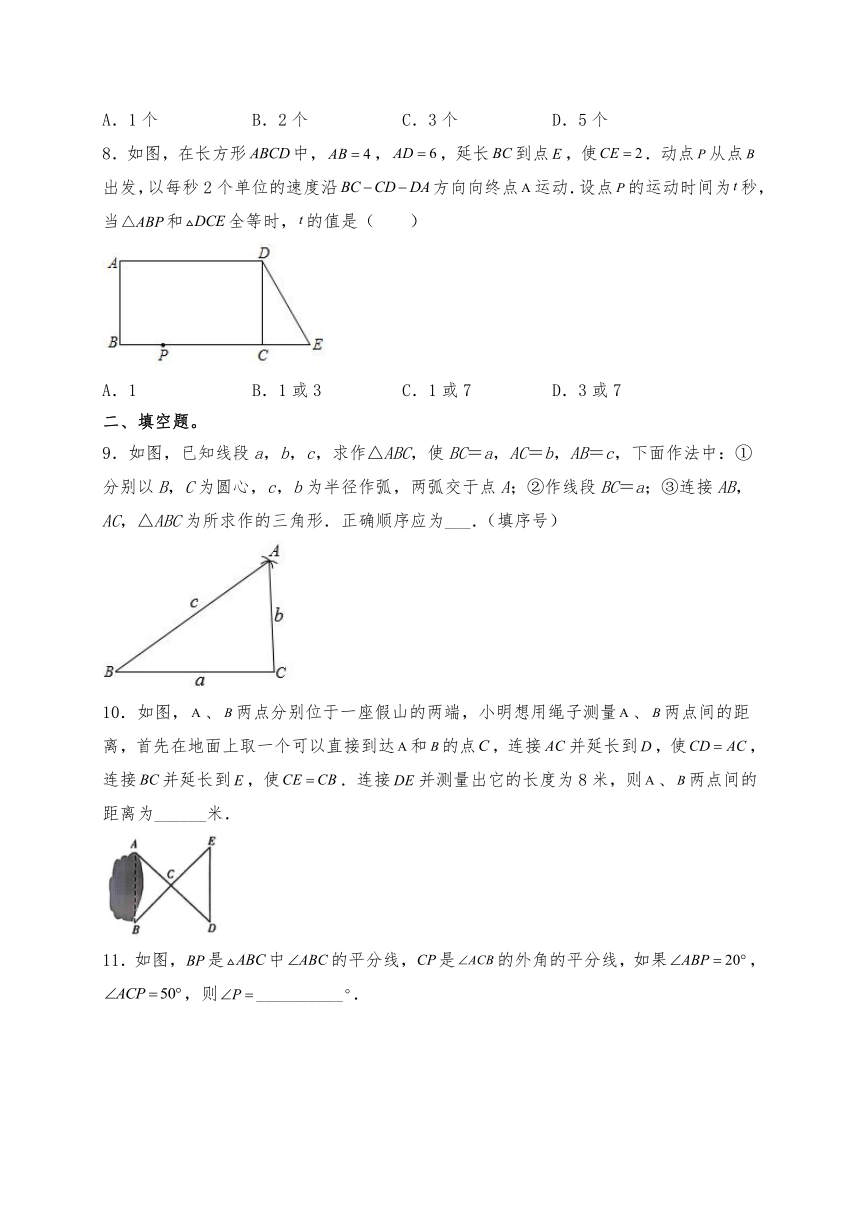
8.如图,在长方形中,,,延长到点,使.动点从点出发,以每秒2个单位的速度沿方向向终点运动.设点的运动时间为秒,当和全等时,的值是( )
A.1 B.1或3 C.1或7 D.3或7
二、填空题。
9.如图,已知线段a,b,c,求作△ABC,使BC=a,AC=b,AB=c,下面作法中:①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;②作线段BC=a;③连接AB,AC,△ABC为所求作的三角形.正确顺序应为___.(填序号)
10.如图,、两点分别位于一座假山的两端,小明想用绳子测量、两点间的距离,首先在地面上取一个可以直接到达和的点,连接并延长到,使,连接并延长到,使.连接并测量出它的长度为8米,则、两点间的距离为______米.
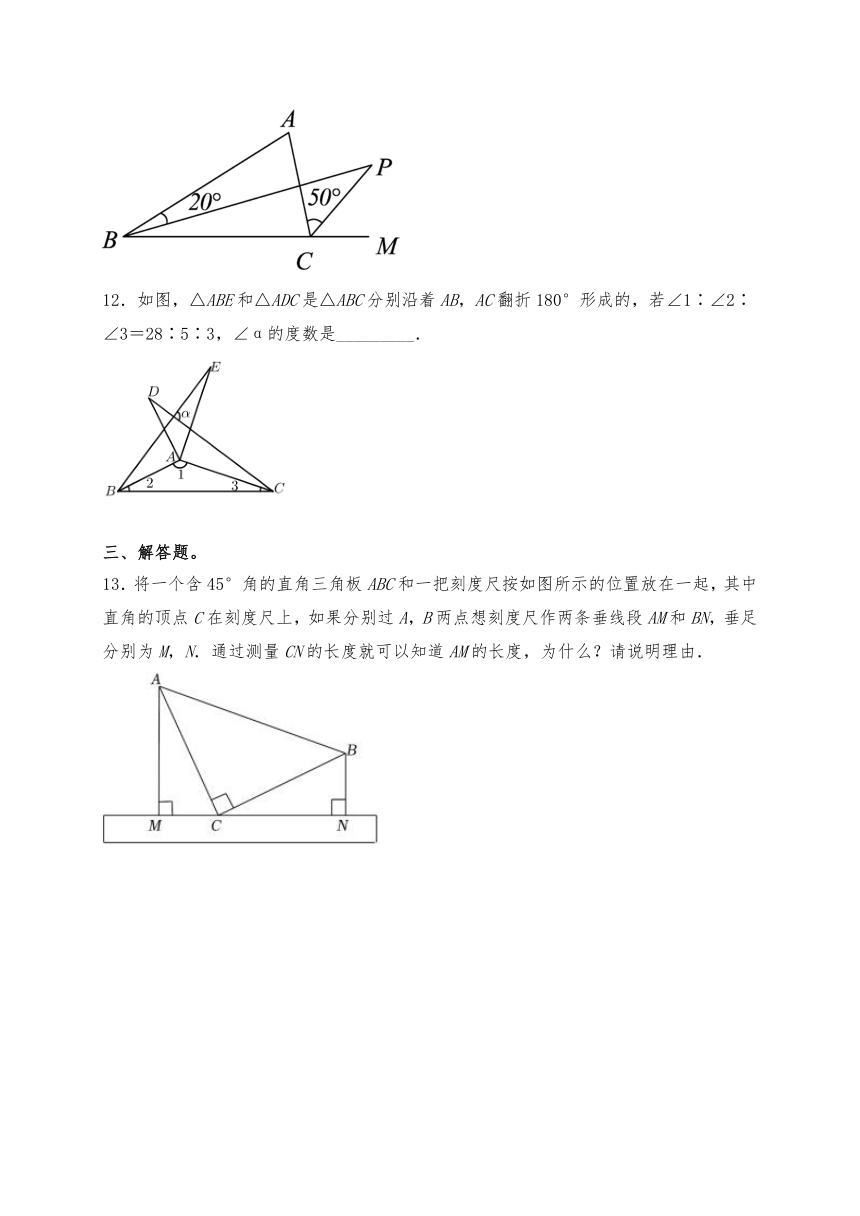
11.如图,是中的平分线,是的外角的平分线,如果,,则__________.
12.如图,△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,∠α的度数是_________.
三、解答题。
13.将一个含45°角的直角三角板ABC和一把刻度尺按如图所示的位置放在一起,其中直角的顶点C在刻度尺上,如果分别过A,B两点想刻度尺作两条垂线段AM和BN,垂足分别为M,N.通过测量CN的长度就可以知道AM的长度,为什么?请说明理由.
14.如图,在△ABC和△DCE中,,,点A,C,D依次在同一直线上,且.
(1)求证:△ABC≌△DCE.
(2)连结AE,当,时,求△ACE的面积.
15.问题提出:学习了三角形全等的判定方法“”“ ”“ ”“ ”和“”后,某小组同学探究了如下问题:当两个三角形满足两边和其中一边的对角分别相等时,这两个三角形是否全等.
初步思考:他们先用符号语言表示了这个问题:在和中,,,.然后,对进行分类,可分为“是直角、钝角、锐角”三种情况进行探究.
深入探究:过程如下,请你将这个小组同学的探究过程补充完整.
(1)第一种情况:当是直角时,.
如图1,在和中,,,,根据 ,可以知道.
(2)第二种情况:当是钝角时,.
如图2,在和中,,,,且,都是钝角,求证:.
(3)第三种情况:当是锐角时,和不一定全等.
在和中,,,,且,都是锐角,请你用尺规在图3中作出,使和不全等.(不写作法,保留作图痕迹)
(4)在(3)中,与的大小关系还要满足什么条件,就可以使?请根据以上作图过程直接写出结论.
答案
一、选择题。
C.A.C.A.A.A.C.C.
二、填空题。
9.②①③.
10.8.
11..
12.80°
三、解答题。
13.
解:AM=CN,
证明如下:
∵一个45°角的直角三角板ABC,
∴AC=BC.
∵A、B两点作两条垂线段AM和BN,
∴∠ACM+∠MAC=90°,∠ACM+∠BCN=90°.
∴∠MAC=∠BCN.
∵∠AMC=∠CNB,
∴△ACM≌△CBN(AAS).
∴AM=CN.
14.
(1)证明:∵AB∥DE,
∴∠BAC=∠D,
在△ABC和△DCE中,
,
∴△ABC≌△DCE(AAS);
(2)解:由(1)得:△ABC≌△DCE,
∴BC=CE=5,
∴△ACE的面积为×12×5=30.
15.
(1)解:∵∠B=∠E=90°,
∴△ABC和△DEF是直角三角形,
∵AC=DF,AB=DE,
∴Rt△ABC≌Rt△DEF(HL),
故答案为:HL;
(2)证明:如图2,过点A作AG⊥CB交CB的延长线于点G,过点D作DH⊥FE交FE的延长线于点H.
则∠AGB=∠DHE=90°,
∵∠ABC=∠DEF,
∴∠ABG=∠DEH,
∵AB=DE,
∴△AGB≌△DHE(AAS),
∴AG=DH,
∵AC=DF,
∴Rt△ACG≌Rt△DFH(HL),
∴∠C=∠F,
又∵∠ABC=∠DEF,AB=DE,
∴△ABC≌△DEF(AAS);
(3)解:如图3,△DEF即为所求;
(4)解:∠B≥∠C,理由如下:
由图3可知,∠C=∠AFC=∠B+∠BAF,
∴∠C>∠B,
∴当∠B≥∠C时,△ABC就唯一确定了,
则△ABC≌△DEF.
一、选择题。
1.在下列各组图形中,是全等的图形是( )
A. B.
C. D.
2.已知,图中的虚线部分是小玉作的辅助线,则下列结论正确的是( )
A.CD是边AB上的高 B.CD是边AC上的高
C.BD是边CB上的高 D.BD是边AC上的高
3.如图,△ABC≌△ADE,∠DAC=90°,∠BAE=140°,BC、DE相交于点F,则∠DAB的大小为( )
A.15° B.20° C.25° D.30°
4.在△ABC和△DCB中,,添加一个条件,不能证明△ABC和△DCB全等的是( )
A. B. C. D.
5.如图,用直尺和圆规作一个三角形O1A1B1,使得O1A1B1≌OAB的示意图,依据( )定理可以判定两个三角形全等
A.SSS B.SAS C.ASA D.AAS
6.为测量一池塘两端A,B间的距离,甲、乙两位同学分别设计了两种不同的方案.
甲:如图1,先过点B作的垂线,再在射线上取C,D两点,使,接着过点D作的垂线,交的延长线于点E,则测出的长即为A,B间的距离;
乙:如图2,先确定直线,过点B作射线,在射线上找可直接到达点A的点D,连接,作,交直线于点C,则测出的长即为A,B间的距离,则下列判断正确的是( )
A.只有甲同学的方案可行 B.只有乙同学的方案可行
C.甲、乙同学的方案均可行 D.甲、乙同学的方案均不可行
7.已知的三边分别为a,b,c,若,c的长为偶数,则满足条件的c的值有( )
A.1个 B.2个 C.3个 D.5个
8.如图,在长方形中,,,延长到点,使.动点从点出发,以每秒2个单位的速度沿方向向终点运动.设点的运动时间为秒,当和全等时,的值是( )
A.1 B.1或3 C.1或7 D.3或7
二、填空题。
9.如图,已知线段a,b,c,求作△ABC,使BC=a,AC=b,AB=c,下面作法中:①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;②作线段BC=a;③连接AB,AC,△ABC为所求作的三角形.正确顺序应为___.(填序号)
10.如图,、两点分别位于一座假山的两端,小明想用绳子测量、两点间的距离,首先在地面上取一个可以直接到达和的点,连接并延长到,使,连接并延长到,使.连接并测量出它的长度为8米,则、两点间的距离为______米.
11.如图,是中的平分线,是的外角的平分线,如果,,则__________.
12.如图,△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,∠α的度数是_________.
三、解答题。
13.将一个含45°角的直角三角板ABC和一把刻度尺按如图所示的位置放在一起,其中直角的顶点C在刻度尺上,如果分别过A,B两点想刻度尺作两条垂线段AM和BN,垂足分别为M,N.通过测量CN的长度就可以知道AM的长度,为什么?请说明理由.
14.如图,在△ABC和△DCE中,,,点A,C,D依次在同一直线上,且.
(1)求证:△ABC≌△DCE.
(2)连结AE,当,时,求△ACE的面积.
15.问题提出:学习了三角形全等的判定方法“”“ ”“ ”“ ”和“”后,某小组同学探究了如下问题:当两个三角形满足两边和其中一边的对角分别相等时,这两个三角形是否全等.
初步思考:他们先用符号语言表示了这个问题:在和中,,,.然后,对进行分类,可分为“是直角、钝角、锐角”三种情况进行探究.
深入探究:过程如下,请你将这个小组同学的探究过程补充完整.
(1)第一种情况:当是直角时,.
如图1,在和中,,,,根据 ,可以知道.
(2)第二种情况:当是钝角时,.
如图2,在和中,,,,且,都是钝角,求证:.
(3)第三种情况:当是锐角时,和不一定全等.
在和中,,,,且,都是锐角,请你用尺规在图3中作出,使和不全等.(不写作法,保留作图痕迹)
(4)在(3)中,与的大小关系还要满足什么条件,就可以使?请根据以上作图过程直接写出结论.
答案
一、选择题。
C.A.C.A.A.A.C.C.
二、填空题。
9.②①③.
10.8.
11..
12.80°
三、解答题。
13.
解:AM=CN,
证明如下:
∵一个45°角的直角三角板ABC,
∴AC=BC.
∵A、B两点作两条垂线段AM和BN,
∴∠ACM+∠MAC=90°,∠ACM+∠BCN=90°.
∴∠MAC=∠BCN.
∵∠AMC=∠CNB,
∴△ACM≌△CBN(AAS).
∴AM=CN.
14.
(1)证明:∵AB∥DE,
∴∠BAC=∠D,
在△ABC和△DCE中,
,
∴△ABC≌△DCE(AAS);
(2)解:由(1)得:△ABC≌△DCE,
∴BC=CE=5,
∴△ACE的面积为×12×5=30.
15.
(1)解:∵∠B=∠E=90°,
∴△ABC和△DEF是直角三角形,
∵AC=DF,AB=DE,
∴Rt△ABC≌Rt△DEF(HL),
故答案为:HL;
(2)证明:如图2,过点A作AG⊥CB交CB的延长线于点G,过点D作DH⊥FE交FE的延长线于点H.
则∠AGB=∠DHE=90°,
∵∠ABC=∠DEF,
∴∠ABG=∠DEH,
∵AB=DE,
∴△AGB≌△DHE(AAS),
∴AG=DH,
∵AC=DF,
∴Rt△ACG≌Rt△DFH(HL),
∴∠C=∠F,
又∵∠ABC=∠DEF,AB=DE,
∴△ABC≌△DEF(AAS);
(3)解:如图3,△DEF即为所求;
(4)解:∠B≥∠C,理由如下:
由图3可知,∠C=∠AFC=∠B+∠BAF,
∴∠C>∠B,
∴当∠B≥∠C时,△ABC就唯一确定了,
则△ABC≌△DEF.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
