北师大版七年级数学下册试题 第五章 《生活中的轴对称》单元测试卷 (含答案)
文档属性
| 名称 | 北师大版七年级数学下册试题 第五章 《生活中的轴对称》单元测试卷 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 753.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 10:43:36 | ||
图片预览



文档简介
第五章 《生活中的轴对称》单元测试卷
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
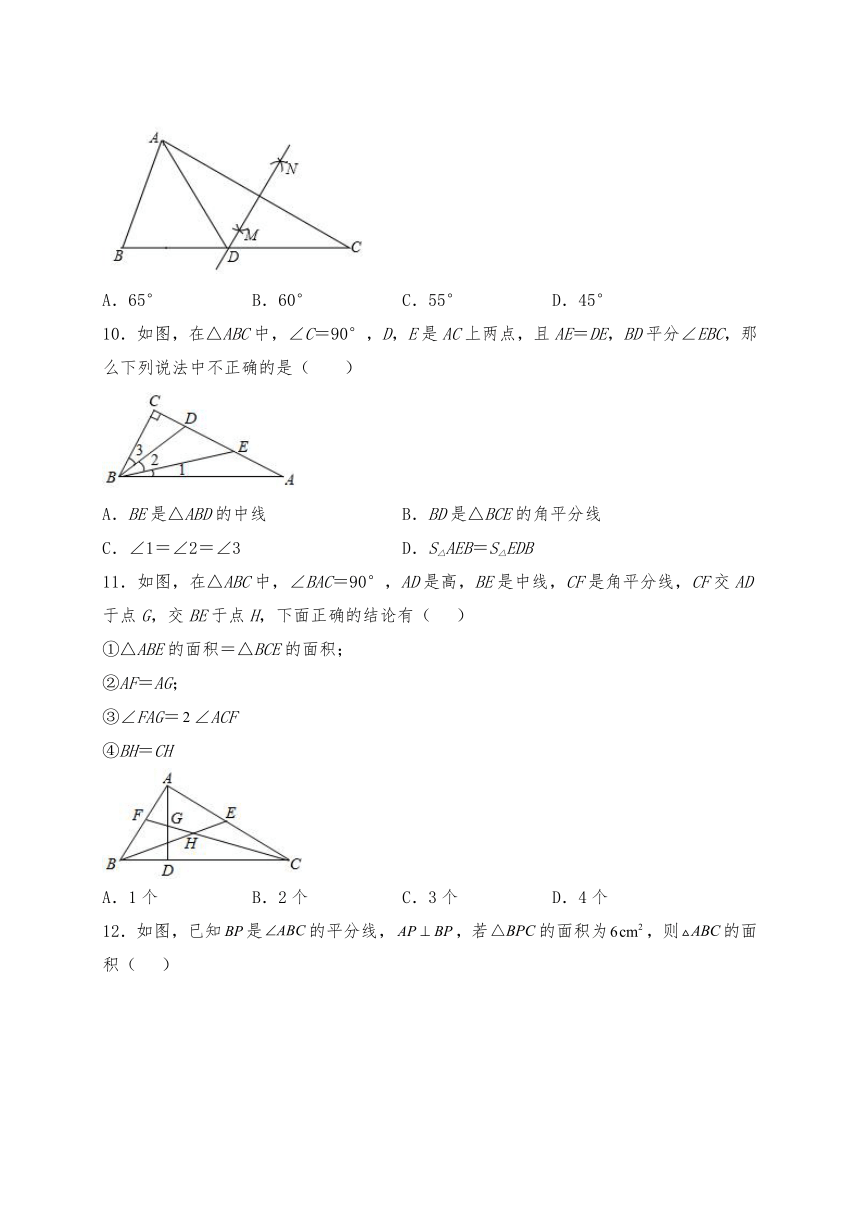
1.在学习《图形变化的简单应用》这一节时,老师要求同学们利用图形变化设计图案.下列设计的图案中,不是轴对称图形的是( )
A. B. C. D.
2.将一张长方形纸条ABCD沿EF折叠后,ED交BF于点G.若∠BGE=130°,则∠EFC的度数是( )
A.110° B.115° C.120° D.125°
3.如图是一只停放在平静水面上的小船,则它在水中的倒影表示正确的是( )
A. B.
C. D.
4.平面直角坐标系内的点A(﹣3,﹣2)与点B(3,﹣2)关于( )
A.y轴对称 B.x轴对称 C.原点对称 D.无法确定
5.如图,△ABC与关于直线MN对称,P为MN上任一点,下列结论中错误的是( )
A.是等腰三角形 B.垂直平分,
C.△ABC与面积相等 D.直线AB、的交点不一定在MN上
6.如图,点为内一点,分别作点关于、的对称点,,连接交于,交于,,则的周长为( )
A.16 B.15 C.14 D.13
7.如图,,,分别是的高、角平分线、中线,则下列各式中错误的是( )
A. B. C. D.
8.已知,其内部有一点,它关于,的对称点分别为,,则是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.等腰直角三角形
9.如图,△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N作直线MN,交BC于点D,连结AD,则∠BAD的度数为( )
A.65° B.60° C.55° D.45°
10.如图,在△ABC中,∠C=90°,D,E是AC上两点,且AE=DE,BD平分∠EBC,那么下列说法中不正确的是( )
A.BE是△ABD的中线 B.BD是△BCE的角平分线
C.∠1=∠2=∠3 D.S△AEB=S△EDB
11.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面正确的结论有( )
①△ABE的面积=△BCE的面积;
②AF=AG;
③∠FAG=∠ACF
④BH=CH
A.1个 B.2个 C.3个 D.4个
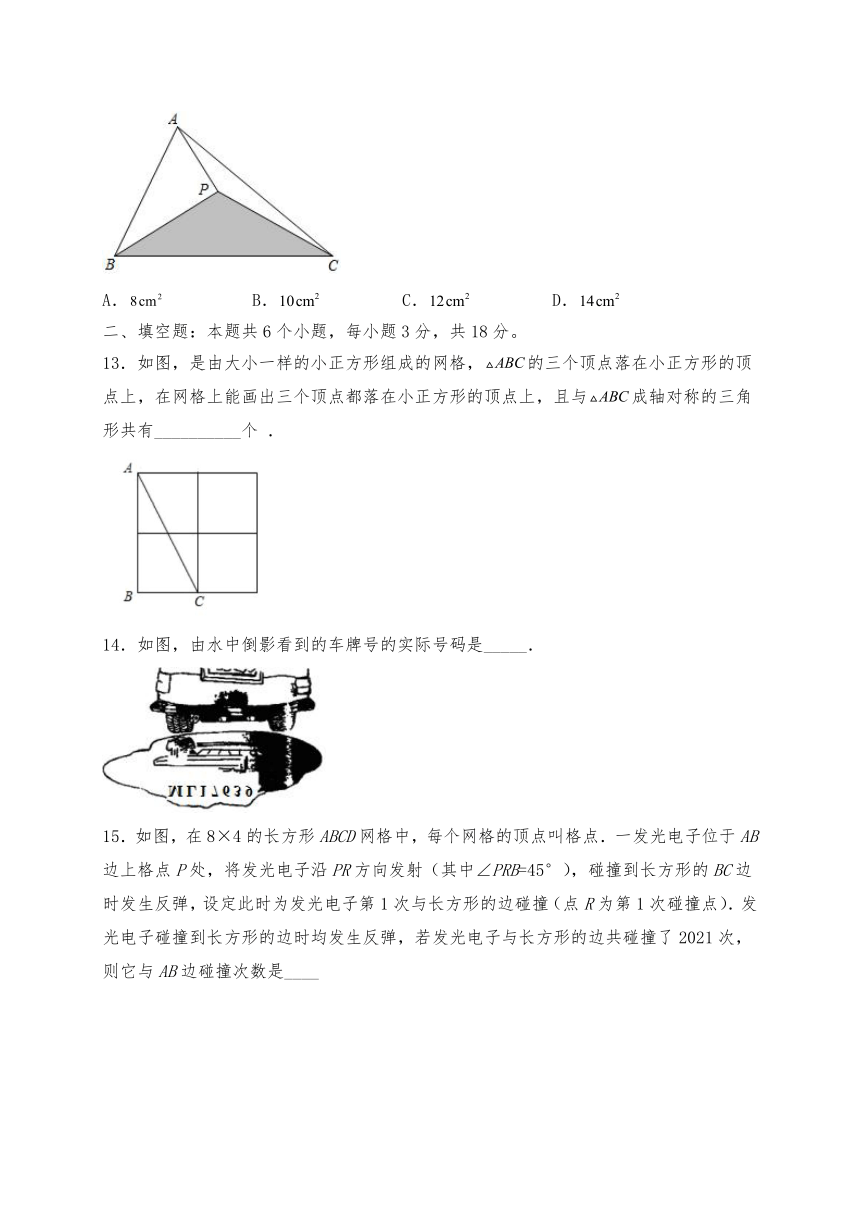
12.如图,已知是的平分线,,若的面积为,则的面积( )
A. B. C. D.
二、填空题:本题共6个小题,每小题3分,共18分。
13.如图,是由大小一样的小正方形组成的网格,的三个顶点落在小正方形的顶点上,在网格上能画出三个顶点都落在小正方形的顶点上,且与成轴对称的三角形共有__________个 .
14.如图,由水中倒影看到的车牌号的实际号码是_____.
15.如图,在8×4的长方形ABCD网格中,每个网格的顶点叫格点.一发光电子位于AB边上格点P处,将发光电子沿PR方向发射(其中∠PRB=45°),碰撞到长方形的BC边时发生反弹,设定此时为发光电子第1次与长方形的边碰撞(点R为第1次碰撞点).发光电子碰撞到长方形的边时均发生反弹,若发光电子与长方形的边共碰撞了2021次,则它与AB边碰撞次数是____
16.如图,长方形纸片ABCD,点E为边AB上一点,连接CE、DE.将∠AED沿ED对折,点A落在点A′处;将∠BEC沿EC对折,点B落在点B′处.若∠A′EB′=α.下列结论:①若∠AED=48°,∠BEC=58°,则∠CED=72°;②∠AED+∠BEC﹣∠CED=α;③若∠CEA′=2∠DEB′=α,则∠DEB′=15°;④若A′E平分∠CEB′,则∠DEB′=90°﹣α.其中一定正确的有 _____(填序号即可).
17.三角形的一个外角是100°,则与它不相邻的两内角平分线夹角(钝角)是 _____.
18.△ABC中,∠ABC和∠ACB的平分线交于点O,OD⊥BC于D,ABC的面积18,AB=6,AC=8,OD=2,则BC的长是_____.
三、解答题(19题6分,其余每题8分,共46分)
19.如图,是由边长为1的小正方形组成的网格,每个小正方形的顶点叫做格点,点、、、均在格点上,在网格中将点按下列步骤移动:
第一步:点绕点顺时针旋转得到点
第二步:点绕点顺时针旋转得到点;
第三步:点绕点顺时针旋转回到点;
(1)请用圆规画出点→→→经过的路径;
(2)所画图形是______对称图形;
(3)写出所画图形围成的面积.(结果保留)
面积:
20.如图,将ABC分别沿AB,AC翻折得到ABD和AEC,线段BD与AE交于点F,连接BE.
(1)若∠ABC=20°,∠ACB=30°,求∠DAE及∠BFE的度数.
(2)若BD所在的直线与CE所在的直线互相垂直,求∠CAB的度数.
21.如图,P为内一定点,M、N分别是射线OA、OB上的点,
(1)当周长最小时,在图中画出(保留作图痕迹);
(2)在(1)的条件下,已知,求的度数.
22.如图1,长方形纸片ABCD(AD>AB),点O位于边BC上,点E位于边AD上,将纸片沿OE折叠,点C、D的对应点分别为点C′、D′.
(1)当点C′与点A重合时,如图2,如果AD=12,CD=8,联结CE,那么△CDE的周长是 ;
(2)如果点F位于边AB上,将纸片沿OF折叠,点B的对应点为点B′.
①当点B′恰好落在线段OC′上时,如图3,那么∠EOF的度数为 ;(直接填写答案)
②当∠B′OC′=20°时,作出图形,并写出∠EOF的度数.
23.如图1,在Rt△ABC中,∠ABC=90°,AB=BC,D为BC边上一点,连接AD,将△ABD沿AB翻折得到△ABE,过点E作AD的垂线,垂足为F,延长EF交AC于G.
(1)求证:EA=EG;
(2)连接DG.
①如图2,当DG⊥AC时,试判断BD与CD的数量关系,并说明理由;
②若AB=5,△EDG的面积为4,请直接写出△CDG的面积.
24.现分别过线段的端点A,B作直线,,且AP//PQ,,的平分线交于点C,过点C的直线l分别交,于点D,E.
(1)求证:是直角三角形;
(2)图1.当直线时,试判断线段之间有怎样的关系并证明;
(3)图2.直线l与不垂直.若,求的长度.
答案
一、选择题。
C.B.A.A.D.B.C.D.A.CC.C.
二、填空题。
13.5.
14.MLI7639
15.673.
16.②③.
17.130°.
18.4.
三、解答题
19.解:(1)点→→→经过的路径如图所示.
(2)根据图形可得,该图形是轴对称图形;
故答案为:轴.
(3)由题意可得:
面积为:(πr2 BD1 BD2)×4=(π×42-×4×4)×4=16π 32
故答案为:.
20.
解:(1)∵,,
∴,
∵,
∴,
∴,
∵,
∴;
(2)∵BD所在直线与CE所在直线互相垂直,
∴,
由翻折的性质可得,,
∴,
∴.
21.
解:(1)作P关于OA,OB的对称点P1,P2.连接OP1,OP2.分别交OA、OB于点M、N,△PMN的周长为P1 P2长,此时周长最短;
(2)连接P1O、P2O,
∵PP1关于OA对称,
∴∠P1OP=2∠MOP,∠OP1M=∠OPM,
同理,∠P2OP=2∠NOP,∠OP2N=∠OPN,
∴∠P1OP2=2∠AOB,
∵∠OPN+∠OPM=∠OP2N+∠OP1M=110°,
∴∠P1OP2=180°﹣110°=70°,
∴∠AOB=35°.
22.
(1)
解:如图2中,点C′与点A重合时,
由翻折的性质可知,EA=EC,
∴DE+EC=DE+EA=AD=12,
∴△CDE的周长=DE+EC+CD=12+8=20.
故答案为:20;
(2)
①如图,
由翻折的性质可知,∠BOF=∠B′OF,∠EOC=∠EOC′,
∵∠BOC=180°,
∴∠EOF=∠EOB′+∠FOB′=(∠COB′+∠BOB′)=∠BOC=90°.
故答案为:90°;
②如图,当OB′在OC′的下方时,
∵∠B′OC′=20°,
∴∠BOB′+∠COC′=180°﹣20°=160°,
∵∠FOB′=∠BOB′,∠EOC′=∠COC′,
∴∠FOB′+∠EOC′=×160°=80°,
∴∠EOF=∠FOB′+∠EOC′+∠B′OC′=100°.
如图,当OB′在OC′的上方时,
∵∠B′OC′=20°,
∴∠BOB′+∠COC′=180°+20°=200°,
∵∠FOB′=∠BOB′,∠EOC′=∠COC′,
∴∠FOB′+∠EOC′=×200°=100°,
∴∠EOF=∠FOB′+∠EOC′﹣∠B′OC′=80°.
综上所述,∠EOF的度数为100°或80°
23.
(1)证明:由折叠得∠BAE=∠BAD,∠AED=∠ADE,
∵EG⊥AD,
∴∠AFE=∠ABC=∠ABE=90°,
∵∠AED+∠BAE=∠ADE+∠DEG=90°,
∴∠BAE=∠DEG,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠BAC=∠ACB,
∴∠BAC+∠BAE=∠ACB+∠DEG,即∠EAC=∠EGA,
∴EA=EG;
(2)①过点G作GN⊥BC于N,则∠ENG=∠ABE=90°,
∵AE=AD,AE=EG,
∴AE=EG,
∵∠BAE=∠NEG,
∴△ABE≌△ENG,
∴GN=BE,
∵DG⊥AC,∠BAC=∠ACB=45°,NG⊥AC,
∴ND=NC=,
∵BE=BD,
∴BD=;
②由①知EB=BD=DN=NC,
∴ED=DC,
∵△EDG的面积=4,
∴△CDG的面积=.
24.(1)∵AP//PQ,
∴.
∵AC和BC分别为,的平分线,
∴,,
∴,即,
∴,
∴是直角三角形;
(2)如图,过点C作于点F.
∵,
∴.
∵AC和BC分别为,的平分线,
∴.
又∵在和中,AC=AC、在和中,BC=BC,
∴、,
∴、.
∵,
∴;
(3)如图,在线段上截取AG=AD,连接CG.
根据题意和所作辅助线可知在和中,
∴,
∴,.
∵AP//PQ,
∴.
∵,
∴.
又∵, ,
∴,
∴,
∴.
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在学习《图形变化的简单应用》这一节时,老师要求同学们利用图形变化设计图案.下列设计的图案中,不是轴对称图形的是( )
A. B. C. D.
2.将一张长方形纸条ABCD沿EF折叠后,ED交BF于点G.若∠BGE=130°,则∠EFC的度数是( )
A.110° B.115° C.120° D.125°
3.如图是一只停放在平静水面上的小船,则它在水中的倒影表示正确的是( )
A. B.
C. D.
4.平面直角坐标系内的点A(﹣3,﹣2)与点B(3,﹣2)关于( )
A.y轴对称 B.x轴对称 C.原点对称 D.无法确定
5.如图,△ABC与关于直线MN对称,P为MN上任一点,下列结论中错误的是( )
A.是等腰三角形 B.垂直平分,
C.△ABC与面积相等 D.直线AB、的交点不一定在MN上
6.如图,点为内一点,分别作点关于、的对称点,,连接交于,交于,,则的周长为( )
A.16 B.15 C.14 D.13
7.如图,,,分别是的高、角平分线、中线,则下列各式中错误的是( )
A. B. C. D.
8.已知,其内部有一点,它关于,的对称点分别为,,则是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.等腰直角三角形
9.如图,△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N作直线MN,交BC于点D,连结AD,则∠BAD的度数为( )
A.65° B.60° C.55° D.45°
10.如图,在△ABC中,∠C=90°,D,E是AC上两点,且AE=DE,BD平分∠EBC,那么下列说法中不正确的是( )
A.BE是△ABD的中线 B.BD是△BCE的角平分线
C.∠1=∠2=∠3 D.S△AEB=S△EDB
11.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面正确的结论有( )
①△ABE的面积=△BCE的面积;
②AF=AG;
③∠FAG=∠ACF
④BH=CH
A.1个 B.2个 C.3个 D.4个
12.如图,已知是的平分线,,若的面积为,则的面积( )
A. B. C. D.
二、填空题:本题共6个小题,每小题3分,共18分。
13.如图,是由大小一样的小正方形组成的网格,的三个顶点落在小正方形的顶点上,在网格上能画出三个顶点都落在小正方形的顶点上,且与成轴对称的三角形共有__________个 .
14.如图,由水中倒影看到的车牌号的实际号码是_____.
15.如图,在8×4的长方形ABCD网格中,每个网格的顶点叫格点.一发光电子位于AB边上格点P处,将发光电子沿PR方向发射(其中∠PRB=45°),碰撞到长方形的BC边时发生反弹,设定此时为发光电子第1次与长方形的边碰撞(点R为第1次碰撞点).发光电子碰撞到长方形的边时均发生反弹,若发光电子与长方形的边共碰撞了2021次,则它与AB边碰撞次数是____
16.如图,长方形纸片ABCD,点E为边AB上一点,连接CE、DE.将∠AED沿ED对折,点A落在点A′处;将∠BEC沿EC对折,点B落在点B′处.若∠A′EB′=α.下列结论:①若∠AED=48°,∠BEC=58°,则∠CED=72°;②∠AED+∠BEC﹣∠CED=α;③若∠CEA′=2∠DEB′=α,则∠DEB′=15°;④若A′E平分∠CEB′,则∠DEB′=90°﹣α.其中一定正确的有 _____(填序号即可).
17.三角形的一个外角是100°,则与它不相邻的两内角平分线夹角(钝角)是 _____.
18.△ABC中,∠ABC和∠ACB的平分线交于点O,OD⊥BC于D,ABC的面积18,AB=6,AC=8,OD=2,则BC的长是_____.
三、解答题(19题6分,其余每题8分,共46分)
19.如图,是由边长为1的小正方形组成的网格,每个小正方形的顶点叫做格点,点、、、均在格点上,在网格中将点按下列步骤移动:
第一步:点绕点顺时针旋转得到点
第二步:点绕点顺时针旋转得到点;
第三步:点绕点顺时针旋转回到点;
(1)请用圆规画出点→→→经过的路径;
(2)所画图形是______对称图形;
(3)写出所画图形围成的面积.(结果保留)
面积:
20.如图,将ABC分别沿AB,AC翻折得到ABD和AEC,线段BD与AE交于点F,连接BE.
(1)若∠ABC=20°,∠ACB=30°,求∠DAE及∠BFE的度数.
(2)若BD所在的直线与CE所在的直线互相垂直,求∠CAB的度数.
21.如图,P为内一定点,M、N分别是射线OA、OB上的点,
(1)当周长最小时,在图中画出(保留作图痕迹);
(2)在(1)的条件下,已知,求的度数.
22.如图1,长方形纸片ABCD(AD>AB),点O位于边BC上,点E位于边AD上,将纸片沿OE折叠,点C、D的对应点分别为点C′、D′.
(1)当点C′与点A重合时,如图2,如果AD=12,CD=8,联结CE,那么△CDE的周长是 ;
(2)如果点F位于边AB上,将纸片沿OF折叠,点B的对应点为点B′.
①当点B′恰好落在线段OC′上时,如图3,那么∠EOF的度数为 ;(直接填写答案)
②当∠B′OC′=20°时,作出图形,并写出∠EOF的度数.
23.如图1,在Rt△ABC中,∠ABC=90°,AB=BC,D为BC边上一点,连接AD,将△ABD沿AB翻折得到△ABE,过点E作AD的垂线,垂足为F,延长EF交AC于G.
(1)求证:EA=EG;
(2)连接DG.
①如图2,当DG⊥AC时,试判断BD与CD的数量关系,并说明理由;
②若AB=5,△EDG的面积为4,请直接写出△CDG的面积.
24.现分别过线段的端点A,B作直线,,且AP//PQ,,的平分线交于点C,过点C的直线l分别交,于点D,E.
(1)求证:是直角三角形;
(2)图1.当直线时,试判断线段之间有怎样的关系并证明;
(3)图2.直线l与不垂直.若,求的长度.
答案
一、选择题。
C.B.A.A.D.B.C.D.A.CC.C.
二、填空题。
13.5.
14.MLI7639
15.673.
16.②③.
17.130°.
18.4.
三、解答题
19.解:(1)点→→→经过的路径如图所示.
(2)根据图形可得,该图形是轴对称图形;
故答案为:轴.
(3)由题意可得:
面积为:(πr2 BD1 BD2)×4=(π×42-×4×4)×4=16π 32
故答案为:.
20.
解:(1)∵,,
∴,
∵,
∴,
∴,
∵,
∴;
(2)∵BD所在直线与CE所在直线互相垂直,
∴,
由翻折的性质可得,,
∴,
∴.
21.
解:(1)作P关于OA,OB的对称点P1,P2.连接OP1,OP2.分别交OA、OB于点M、N,△PMN的周长为P1 P2长,此时周长最短;
(2)连接P1O、P2O,
∵PP1关于OA对称,
∴∠P1OP=2∠MOP,∠OP1M=∠OPM,
同理,∠P2OP=2∠NOP,∠OP2N=∠OPN,
∴∠P1OP2=2∠AOB,
∵∠OPN+∠OPM=∠OP2N+∠OP1M=110°,
∴∠P1OP2=180°﹣110°=70°,
∴∠AOB=35°.
22.
(1)
解:如图2中,点C′与点A重合时,
由翻折的性质可知,EA=EC,
∴DE+EC=DE+EA=AD=12,
∴△CDE的周长=DE+EC+CD=12+8=20.
故答案为:20;
(2)
①如图,
由翻折的性质可知,∠BOF=∠B′OF,∠EOC=∠EOC′,
∵∠BOC=180°,
∴∠EOF=∠EOB′+∠FOB′=(∠COB′+∠BOB′)=∠BOC=90°.
故答案为:90°;
②如图,当OB′在OC′的下方时,
∵∠B′OC′=20°,
∴∠BOB′+∠COC′=180°﹣20°=160°,
∵∠FOB′=∠BOB′,∠EOC′=∠COC′,
∴∠FOB′+∠EOC′=×160°=80°,
∴∠EOF=∠FOB′+∠EOC′+∠B′OC′=100°.
如图,当OB′在OC′的上方时,
∵∠B′OC′=20°,
∴∠BOB′+∠COC′=180°+20°=200°,
∵∠FOB′=∠BOB′,∠EOC′=∠COC′,
∴∠FOB′+∠EOC′=×200°=100°,
∴∠EOF=∠FOB′+∠EOC′﹣∠B′OC′=80°.
综上所述,∠EOF的度数为100°或80°
23.
(1)证明:由折叠得∠BAE=∠BAD,∠AED=∠ADE,
∵EG⊥AD,
∴∠AFE=∠ABC=∠ABE=90°,
∵∠AED+∠BAE=∠ADE+∠DEG=90°,
∴∠BAE=∠DEG,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠BAC=∠ACB,
∴∠BAC+∠BAE=∠ACB+∠DEG,即∠EAC=∠EGA,
∴EA=EG;
(2)①过点G作GN⊥BC于N,则∠ENG=∠ABE=90°,
∵AE=AD,AE=EG,
∴AE=EG,
∵∠BAE=∠NEG,
∴△ABE≌△ENG,
∴GN=BE,
∵DG⊥AC,∠BAC=∠ACB=45°,NG⊥AC,
∴ND=NC=,
∵BE=BD,
∴BD=;
②由①知EB=BD=DN=NC,
∴ED=DC,
∵△EDG的面积=4,
∴△CDG的面积=.
24.(1)∵AP//PQ,
∴.
∵AC和BC分别为,的平分线,
∴,,
∴,即,
∴,
∴是直角三角形;
(2)如图,过点C作于点F.
∵,
∴.
∵AC和BC分别为,的平分线,
∴.
又∵在和中,AC=AC、在和中,BC=BC,
∴、,
∴、.
∵,
∴;
(3)如图,在线段上截取AG=AD,连接CG.
根据题意和所作辅助线可知在和中,
∴,
∴,.
∵AP//PQ,
∴.
∵,
∴.
又∵, ,
∴,
∴,
∴.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
