北师大版七年级数学下册试题 第五章 《生活中的轴对称》复习卷 (含答案)
文档属性
| 名称 | 北师大版七年级数学下册试题 第五章 《生活中的轴对称》复习卷 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 459.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 10:44:24 | ||
图片预览

文档简介
第五章 《生活中的轴对称》复习卷
一、选择题。
1.下列常见的微信表情包中,不属于轴对称图形的是( )
A. B. C. D.
2.数学课上,小明用尺规在黑板上作∠AOB的平分线,并进行简单的说理,下面是小明的解答过程,则符号“ 、 、☆、 ”代表的内容错误的是( )
已知:∠AOB. 求作:射线OC,使∠AOC=∠BOC. 作法:(1)以点O为圆心,在OA和OB上分别截取OD,OE,使 ; (2)分别以点D,E为圆心、以 为半径作弧,两弧在∠AOB内交于点C; (3)作射线OC.OC就是∠AOB的平分线. 理由: (1)连接EC,DC,则EC=DC,易知△OEC≌△ODC,理由☆; (2)所以∠AOC=∠BOC,理由 .
A. 表示“OD=OE” B. 表示“大于DE的长”
C.☆表示“SAS” D. 表示“全等三角形的对应角相等”
3.如图,小强拿一张正方形的纸,沿图甲中虚线对折一次得图乙,再对折一次得图丙,然后用剪刀沿图丙中的虚线剪去一个角,再打开后的形状是( )
A. B. C. D.
4.在三条边都不相等的三角形中,同一条边上的中线、高和这边所对角的角平分线,最短的是( )
A.角平分线 B.高 C.中线 D.不能确定
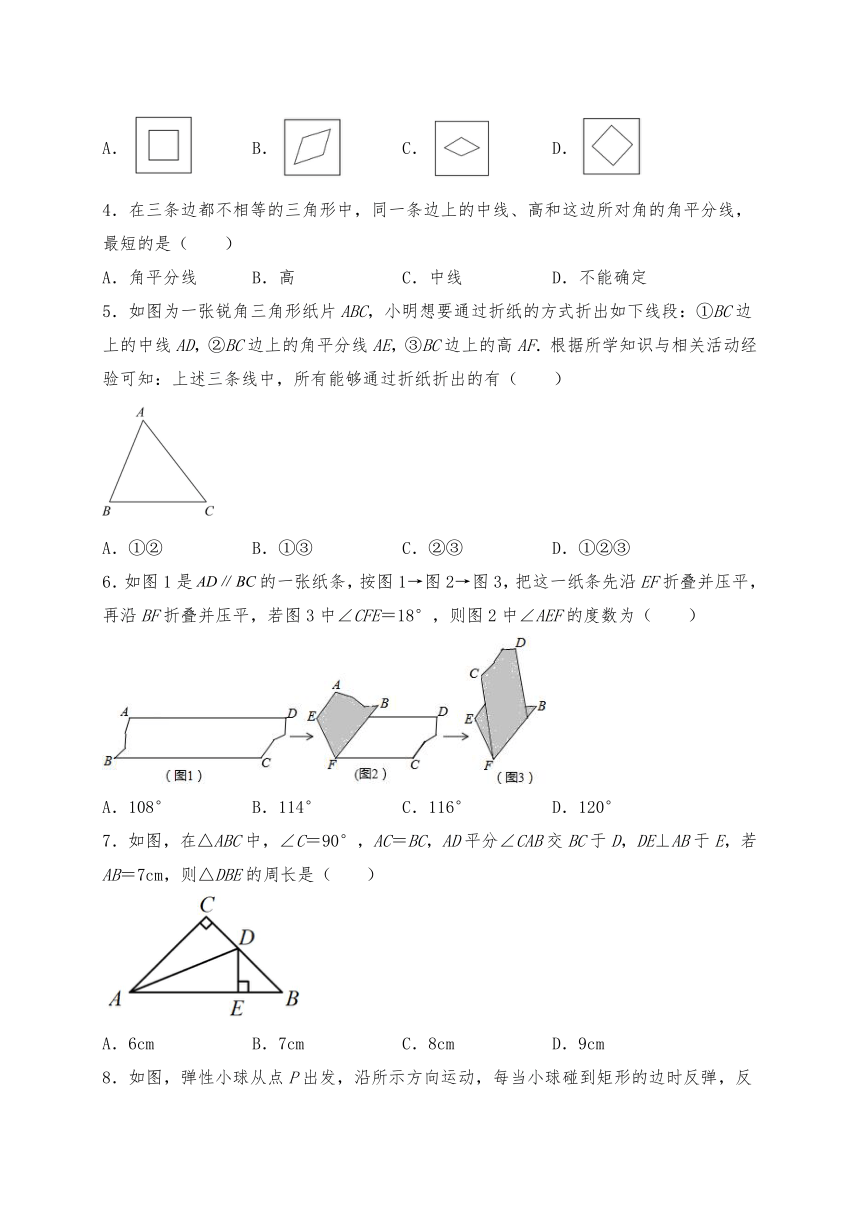
5.如图为一张锐角三角形纸片ABC,小明想要通过折纸的方式折出如下线段:①BC边上的中线AD,②BC边上的角平分线AE,③BC边上的高AF.根据所学知识与相关活动经验可知:上述三条线中,所有能够通过折纸折出的有( )
A.①② B.①③ C.②③ D.①②③
6.如图1是的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
A.108° B.114° C.116° D.120°
7.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,若AB=7cm,则△DBE的周长是( )
A.6cm B.7cm C.8cm D.9cm
8.如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到矩形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到矩形的边时的点为Q,第2次碰到矩形的边时的点为M,….第2022次碰到矩形的边时的点为图中的( )
A.点P B.点Q C.点M D.点N
二、填空题。
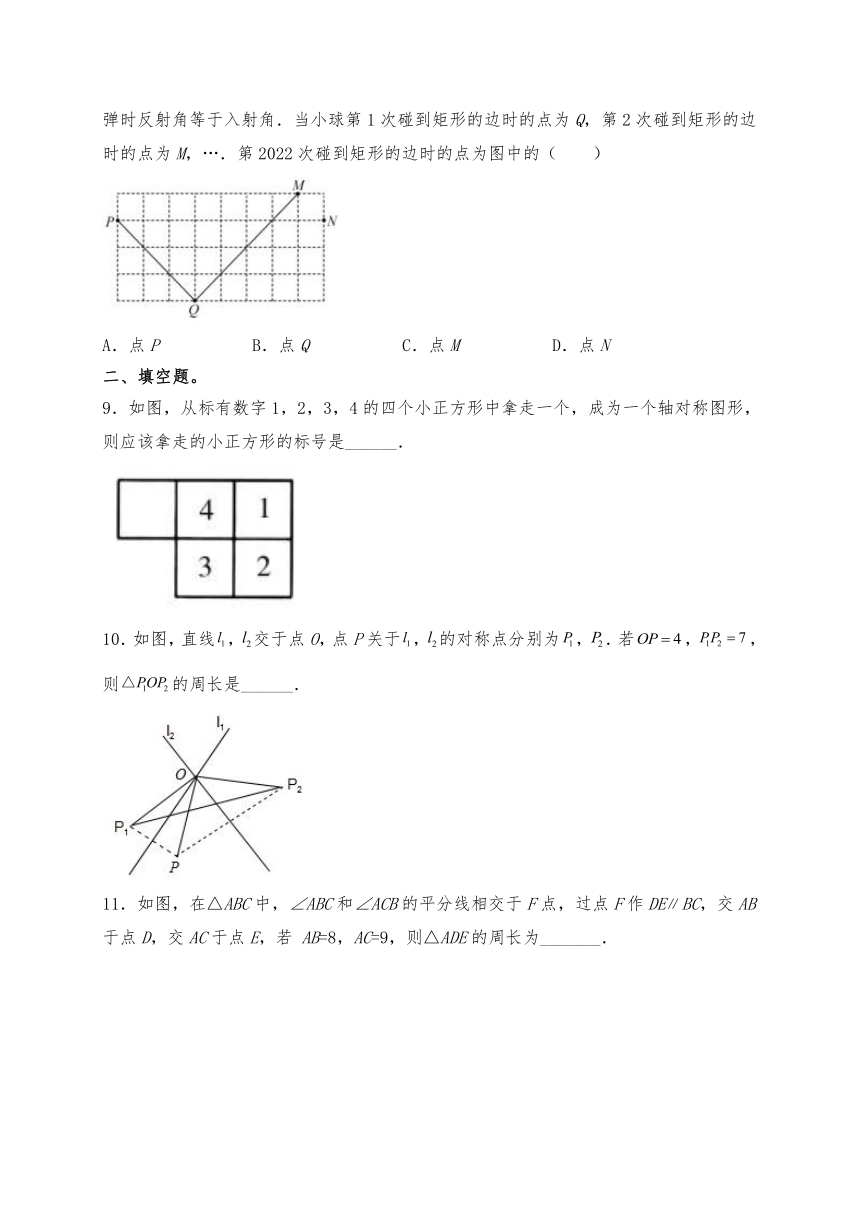
9.如图,从标有数字1,2,3,4的四个小正方形中拿走一个,成为一个轴对称图形,则应该拿走的小正方形的标号是______.
10.如图,直线,交于点O,点P关于,的对称点分别为,.若,,则的周长是______.
11.如图,在△ABC中,∠ABC和∠ACB的平分线相交于F点,过点F作DEBC,交AB于点D,交AC于点E,若 AB=8,AC=9,则△ADE的周长为_______.
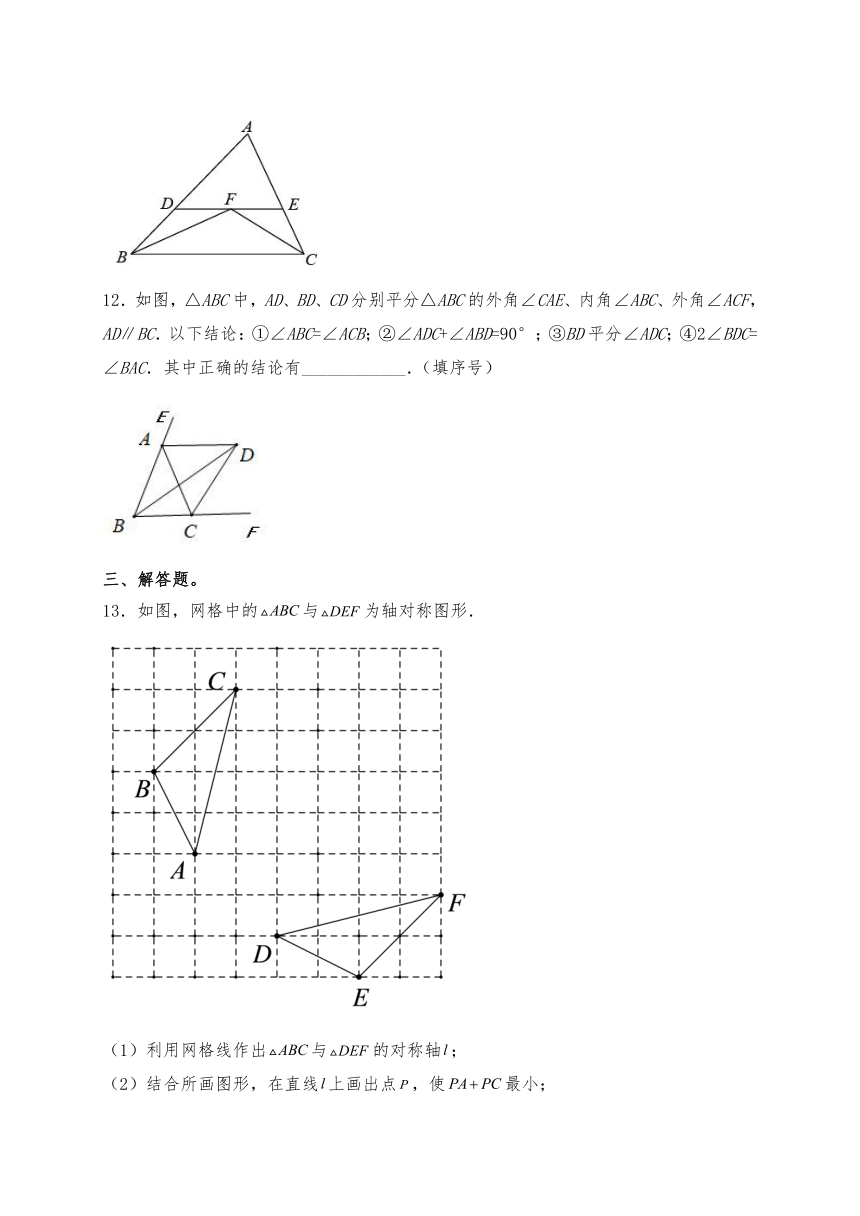
12.如图,△ABC中,AD、BD、CD分别平分△ABC的外角∠CAE、内角∠ABC、外角∠ACF,AD∥BC.以下结论:①∠ABC=∠ACB;②∠ADC+∠ABD=90°;③BD平分∠ADC;④2∠BDC=∠BAC.其中正确的结论有____________.(填序号)
三、解答题。
13.如图,网格中的与为轴对称图形.
(1)利用网格线作出与的对称轴;
(2)结合所画图形,在直线上画出点,使最小;
(3)如果每一个小正方形的边长为,请直接写出的面积________.
14.同学们,我们已经学习了角的平分线的定义,请你用它解决下列问题:
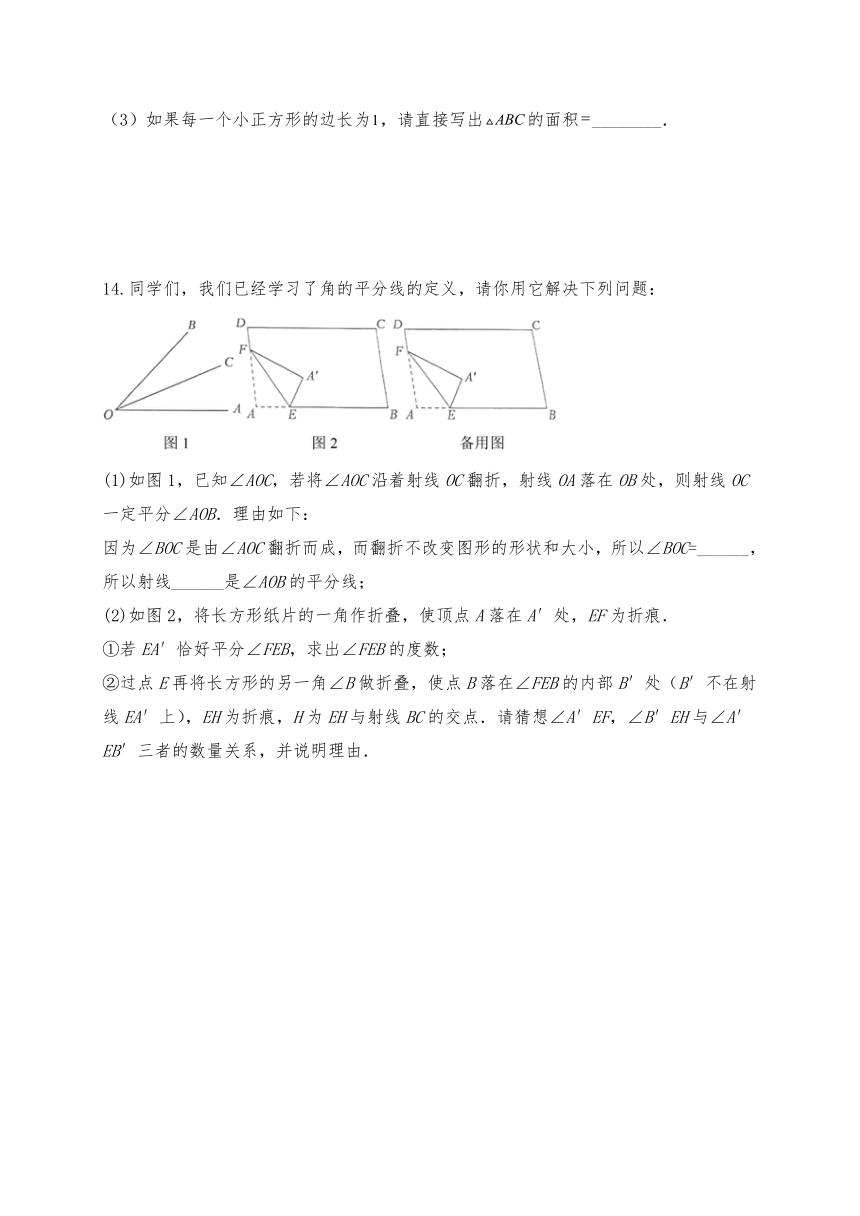
(1)如图1,已知∠AOC,若将∠AOC沿着射线OC翻折,射线OA落在OB处,则射线OC一定平分∠AOB.理由如下:
因为∠BOC是由∠AOC翻折而成,而翻折不改变图形的形状和大小,所以∠BOC=______,所以射线______是∠AOB的平分线;
(2)如图2,将长方形纸片的一角作折叠,使顶点A落在A′处,EF为折痕.
①若EA′恰好平分∠FEB,求出∠FEB的度数;
②过点E再将长方形的另一角∠B做折叠,使点B落在∠FEB的内部B′处(B′不在射线EA′上),EH为折痕,H为EH与射线BC的交点.请猜想∠A′EF,∠B′EH与∠A′EB′三者的数量关系,并说明理由.
15.如图,AD为△ABC的角平分线.
(1)如图1,若CE⊥AD于点F,交AB于点E,AB=8,AC=5.则BE=_______.
(2)如图2,若∠C=2∠B,点E在AB上,且AE=AC,AB=a,AC=b,求CD的长;(用含a、b的式子表示)
(3)如图3,BG⊥AD,点G在AD的延长线上,连接CG,若△ACG的面积是7,求△ABC的面积.
答案
一、选择题。
C.C.B.B.D.B.B.A.
二、填空题。
9.2.
10.15
11.17.
12.①②④.
三、解答题。
13.
(1)如图,连接找到的中点,过这两点作出直线,即为所求对称轴;
(2)找到的对称点,连接,与交于点,点即为所求;
,当共线时, 最小;
(3)
14.
(1)
解:因为∠BOC是由∠AOC翻折而成,而翻折不改变图形的形状和大小,所以∠BOC=∠AOC,所以射线OC是∠AOB的平分线;
故答案为:∠AOC,OC;
(2)
解:①由翻折可知:∠AEF=∠A′EF,
∵EA′恰好平分∠FEB,
∴∠A′EF=∠A′EB,
∵∠AEF+∠A′EF+∠A′EB=180°,
∴3∠AEF=180°,
∴∠AEF=60°,
∴∠FEB=180°﹣60°=120°;
∴∠FEB的度数为120°;
②根据题意点B落在∠FEB的内部B′处(B′不在射线EA′上),EH为折痕,
∴2∠A′EF+2∠B′EH=180°±∠A′EB′,
所以分两种情况讨论:
当EB′落在A′E右侧时,2∠A′EF+∠A′EB′+2∠B′EH=180°,
∴2∠A′EF+2∠B′EH=180°﹣∠A′EB′;
当EB′落在A′E左侧时,2∠A′EF+2∠B′EH﹣∠A′EB′=180°,
∴2∠A′EF+2∠B′EH=180°+∠A′EB′.
综上所述:2∠A′EF+2∠B′EH=180°﹣∠A′EB′或2∠A′EF+2∠B′EH=180°+∠A′EB′.
15.
(1)
解:(1)∵AD是△ABC的平分线,
∴∠BAD=∠CAD,
∵CE⊥AD,
∴∠CFA=∠EFA,
∵在△AEF和△ACF中,
∴△AEF≌△ACF(ASA),
∴AE=AC=5,
∵AB=8,
∴BE=AB AC=8 5=3,
故答案为:3;
(2)
∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ADE和△ADC中
∴△ADE≌△ADC
∴∠C=∠AED,DC=DE
又∵∠C=2∠B,∠AED=∠B+∠BDE
∴∠B=∠BDE
∴DE=BE,
∴DC=DE=BE=AB-AE=AB-AC=a-b;
(3)
如图,分别延长AC,BG交于点H,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵AG⊥BH,
∴∠AGB=∠AGH=90°,
∵在△AGB和△AGH中
,
∴△AGB≌△AGH,
∴BG=HG,
∴,
又∵
∴=14.
一、选择题。
1.下列常见的微信表情包中,不属于轴对称图形的是( )
A. B. C. D.
2.数学课上,小明用尺规在黑板上作∠AOB的平分线,并进行简单的说理,下面是小明的解答过程,则符号“ 、 、☆、 ”代表的内容错误的是( )
已知:∠AOB. 求作:射线OC,使∠AOC=∠BOC. 作法:(1)以点O为圆心,在OA和OB上分别截取OD,OE,使 ; (2)分别以点D,E为圆心、以 为半径作弧,两弧在∠AOB内交于点C; (3)作射线OC.OC就是∠AOB的平分线. 理由: (1)连接EC,DC,则EC=DC,易知△OEC≌△ODC,理由☆; (2)所以∠AOC=∠BOC,理由 .
A. 表示“OD=OE” B. 表示“大于DE的长”
C.☆表示“SAS” D. 表示“全等三角形的对应角相等”
3.如图,小强拿一张正方形的纸,沿图甲中虚线对折一次得图乙,再对折一次得图丙,然后用剪刀沿图丙中的虚线剪去一个角,再打开后的形状是( )
A. B. C. D.
4.在三条边都不相等的三角形中,同一条边上的中线、高和这边所对角的角平分线,最短的是( )
A.角平分线 B.高 C.中线 D.不能确定
5.如图为一张锐角三角形纸片ABC,小明想要通过折纸的方式折出如下线段:①BC边上的中线AD,②BC边上的角平分线AE,③BC边上的高AF.根据所学知识与相关活动经验可知:上述三条线中,所有能够通过折纸折出的有( )
A.①② B.①③ C.②③ D.①②③
6.如图1是的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
A.108° B.114° C.116° D.120°
7.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,若AB=7cm,则△DBE的周长是( )
A.6cm B.7cm C.8cm D.9cm
8.如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到矩形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到矩形的边时的点为Q,第2次碰到矩形的边时的点为M,….第2022次碰到矩形的边时的点为图中的( )
A.点P B.点Q C.点M D.点N
二、填空题。
9.如图,从标有数字1,2,3,4的四个小正方形中拿走一个,成为一个轴对称图形,则应该拿走的小正方形的标号是______.
10.如图,直线,交于点O,点P关于,的对称点分别为,.若,,则的周长是______.
11.如图,在△ABC中,∠ABC和∠ACB的平分线相交于F点,过点F作DEBC,交AB于点D,交AC于点E,若 AB=8,AC=9,则△ADE的周长为_______.
12.如图,△ABC中,AD、BD、CD分别平分△ABC的外角∠CAE、内角∠ABC、外角∠ACF,AD∥BC.以下结论:①∠ABC=∠ACB;②∠ADC+∠ABD=90°;③BD平分∠ADC;④2∠BDC=∠BAC.其中正确的结论有____________.(填序号)
三、解答题。
13.如图,网格中的与为轴对称图形.
(1)利用网格线作出与的对称轴;
(2)结合所画图形,在直线上画出点,使最小;
(3)如果每一个小正方形的边长为,请直接写出的面积________.
14.同学们,我们已经学习了角的平分线的定义,请你用它解决下列问题:
(1)如图1,已知∠AOC,若将∠AOC沿着射线OC翻折,射线OA落在OB处,则射线OC一定平分∠AOB.理由如下:
因为∠BOC是由∠AOC翻折而成,而翻折不改变图形的形状和大小,所以∠BOC=______,所以射线______是∠AOB的平分线;
(2)如图2,将长方形纸片的一角作折叠,使顶点A落在A′处,EF为折痕.
①若EA′恰好平分∠FEB,求出∠FEB的度数;
②过点E再将长方形的另一角∠B做折叠,使点B落在∠FEB的内部B′处(B′不在射线EA′上),EH为折痕,H为EH与射线BC的交点.请猜想∠A′EF,∠B′EH与∠A′EB′三者的数量关系,并说明理由.
15.如图,AD为△ABC的角平分线.
(1)如图1,若CE⊥AD于点F,交AB于点E,AB=8,AC=5.则BE=_______.
(2)如图2,若∠C=2∠B,点E在AB上,且AE=AC,AB=a,AC=b,求CD的长;(用含a、b的式子表示)
(3)如图3,BG⊥AD,点G在AD的延长线上,连接CG,若△ACG的面积是7,求△ABC的面积.
答案
一、选择题。
C.C.B.B.D.B.B.A.
二、填空题。
9.2.
10.15
11.17.
12.①②④.
三、解答题。
13.
(1)如图,连接找到的中点,过这两点作出直线,即为所求对称轴;
(2)找到的对称点,连接,与交于点,点即为所求;
,当共线时, 最小;
(3)
14.
(1)
解:因为∠BOC是由∠AOC翻折而成,而翻折不改变图形的形状和大小,所以∠BOC=∠AOC,所以射线OC是∠AOB的平分线;
故答案为:∠AOC,OC;
(2)
解:①由翻折可知:∠AEF=∠A′EF,
∵EA′恰好平分∠FEB,
∴∠A′EF=∠A′EB,
∵∠AEF+∠A′EF+∠A′EB=180°,
∴3∠AEF=180°,
∴∠AEF=60°,
∴∠FEB=180°﹣60°=120°;
∴∠FEB的度数为120°;
②根据题意点B落在∠FEB的内部B′处(B′不在射线EA′上),EH为折痕,
∴2∠A′EF+2∠B′EH=180°±∠A′EB′,
所以分两种情况讨论:
当EB′落在A′E右侧时,2∠A′EF+∠A′EB′+2∠B′EH=180°,
∴2∠A′EF+2∠B′EH=180°﹣∠A′EB′;
当EB′落在A′E左侧时,2∠A′EF+2∠B′EH﹣∠A′EB′=180°,
∴2∠A′EF+2∠B′EH=180°+∠A′EB′.
综上所述:2∠A′EF+2∠B′EH=180°﹣∠A′EB′或2∠A′EF+2∠B′EH=180°+∠A′EB′.
15.
(1)
解:(1)∵AD是△ABC的平分线,
∴∠BAD=∠CAD,
∵CE⊥AD,
∴∠CFA=∠EFA,
∵在△AEF和△ACF中,
∴△AEF≌△ACF(ASA),
∴AE=AC=5,
∵AB=8,
∴BE=AB AC=8 5=3,
故答案为:3;
(2)
∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ADE和△ADC中
∴△ADE≌△ADC
∴∠C=∠AED,DC=DE
又∵∠C=2∠B,∠AED=∠B+∠BDE
∴∠B=∠BDE
∴DE=BE,
∴DC=DE=BE=AB-AE=AB-AC=a-b;
(3)
如图,分别延长AC,BG交于点H,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵AG⊥BH,
∴∠AGB=∠AGH=90°,
∵在△AGB和△AGH中
,
∴△AGB≌△AGH,
∴BG=HG,
∴,
又∵
∴=14.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
