人教版数学八年级上册 12.2.2三角形全等的判定之边角边(SAS)定理 课件(共12张PPT)
文档属性
| 名称 | 人教版数学八年级上册 12.2.2三角形全等的判定之边角边(SAS)定理 课件(共12张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 641.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 00:00:00 | ||
图片预览




文档简介
(共12张PPT)
12.2.2三角形全等的判定之边角边(SAS)
知识回顾
一、什么是全等三角形?
二、全等三角形有哪些性质?
三、上一节课学习了证明三角形全等的
什么判定条件?
创设情境,引入课题
尺规作图画出一个△A′B′C′,使A′B′=AB,
A′C′=AC,∠A′=∠A (即使两边和它们的夹角
对应相等). 把画好的△A′B′C′剪下,放到△ABC
上,它们全等吗?
交流对话,探求新知
两个三角形全等的一个方法:
两边和它们的夹角对应相等的两个
三角形全等(可以间写成“边角边”
或“SAS”)。
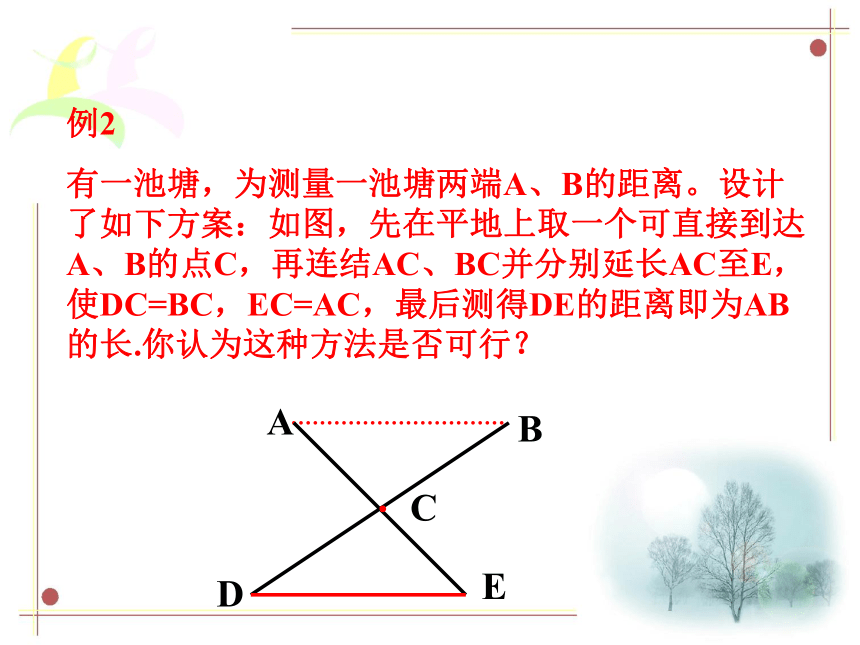
例2
有一池塘,为测量一池塘两端A、B的距离。设计了如下方案:如图,先在平地上取一个可直接到达A、B的点C,再连结AC、BC并分别延长AC至E,使DC=BC,EC=AC,最后测得DE的距离即为AB的长.你认为这种方法是否可行?
C
·
A
E
D
B
应用新知,体验成功
如图是一个平行四边形ABCD,证明△ABC≌△CDA。
A
B
C
D
证明:∵根据平行四边形的性质,
∴BC=DA,∠BCA=∠DAC。
又∵AC=CA,
∴由SAS定理可知,
△ABC≌△CDA。
我们知道,两边和它们的夹角对应相等的两个三角形全等。由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?
再次探究,释疑解惑
做一做:
画一个三角形,使它的一个内角为60度,这个角的对边为 6厘米,另一条边长为5 厘米.
画一个三角形,使它的一个内角为45度,这个角的对边为 3厘米,另一条边长为4厘米.
由“两边及其中一边的对角对应相等”的条件不能判定两个三角形全等.
总结:
巩固练习
(1)小明做了一个如图所示的风筝,测得DE=DF, EH=FH,你能发现哪些结论 并说明理由.
(2)如图,∠1=∠2,AB=AD,AE=AC,求证BC= DE.
再见
12.2.2三角形全等的判定之边角边(SAS)
知识回顾
一、什么是全等三角形?
二、全等三角形有哪些性质?
三、上一节课学习了证明三角形全等的
什么判定条件?
创设情境,引入课题
尺规作图画出一个△A′B′C′,使A′B′=AB,
A′C′=AC,∠A′=∠A (即使两边和它们的夹角
对应相等). 把画好的△A′B′C′剪下,放到△ABC
上,它们全等吗?
交流对话,探求新知
两个三角形全等的一个方法:
两边和它们的夹角对应相等的两个
三角形全等(可以间写成“边角边”
或“SAS”)。
例2
有一池塘,为测量一池塘两端A、B的距离。设计了如下方案:如图,先在平地上取一个可直接到达A、B的点C,再连结AC、BC并分别延长AC至E,使DC=BC,EC=AC,最后测得DE的距离即为AB的长.你认为这种方法是否可行?
C
·
A
E
D
B
应用新知,体验成功
如图是一个平行四边形ABCD,证明△ABC≌△CDA。
A
B
C
D
证明:∵根据平行四边形的性质,
∴BC=DA,∠BCA=∠DAC。
又∵AC=CA,
∴由SAS定理可知,
△ABC≌△CDA。
我们知道,两边和它们的夹角对应相等的两个三角形全等。由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?
再次探究,释疑解惑
做一做:
画一个三角形,使它的一个内角为60度,这个角的对边为 6厘米,另一条边长为5 厘米.
画一个三角形,使它的一个内角为45度,这个角的对边为 3厘米,另一条边长为4厘米.
由“两边及其中一边的对角对应相等”的条件不能判定两个三角形全等.
总结:
巩固练习
(1)小明做了一个如图所示的风筝,测得DE=DF, EH=FH,你能发现哪些结论 并说明理由.
(2)如图,∠1=∠2,AB=AD,AE=AC,求证BC= DE.
再见
