14.1轴对称(2)[上学期]
文档属性
| 名称 | 14.1轴对称(2)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 635.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-15 00:00:00 | ||
图片预览



文档简介
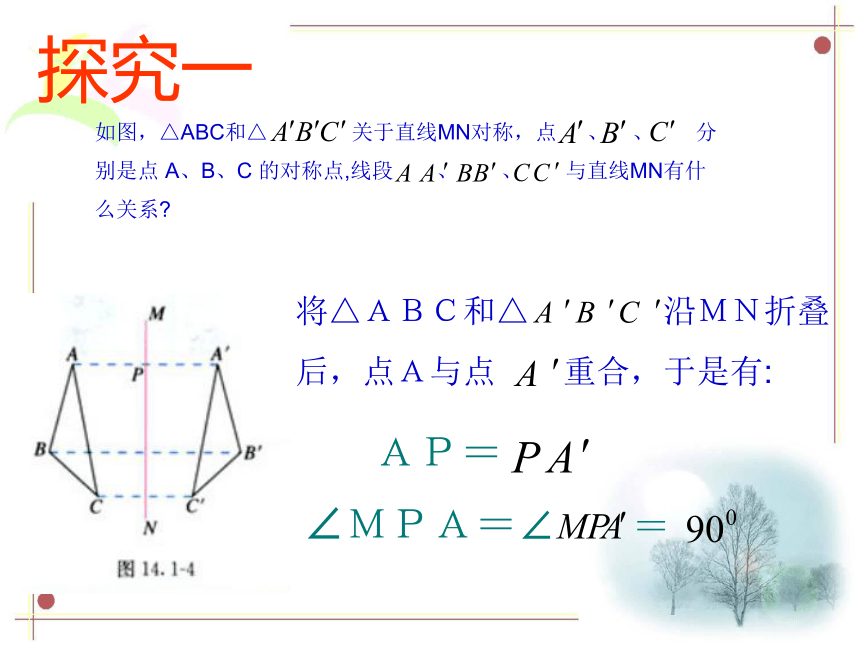
课件17张PPT。14.1 轴对称(2)授课人:沈海尉轴对称图形与轴对称的区别与联系如图,△ABC和△ 关于直线MN对称,点 、 、 分
别是点 A、B、C 的对称点,线段 、 、 与直线MN有什
么关系? 探究一AP=∠MPA=∠ =将△ABC和△ 沿MN折叠
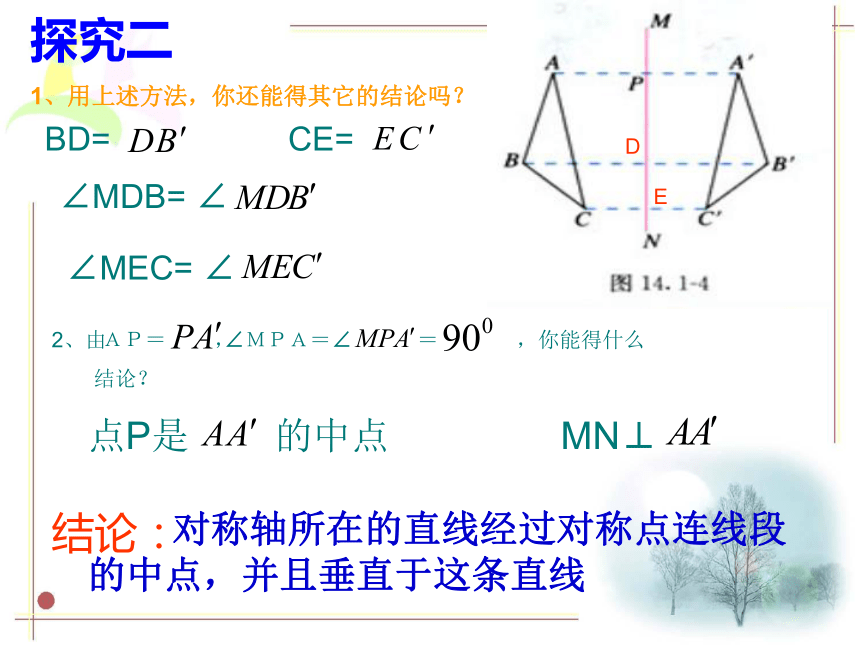
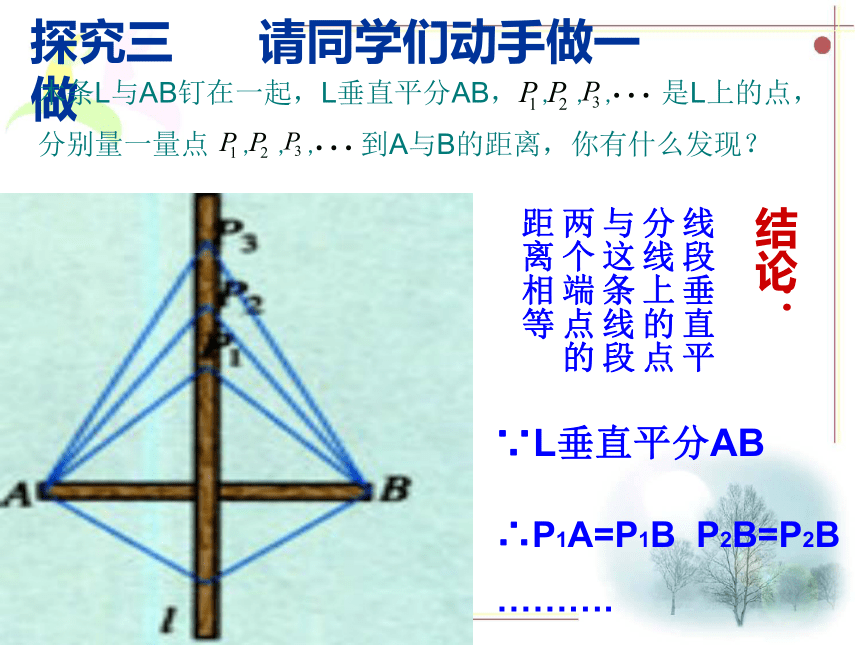
后,点A与点 重合,于是有:探究二1、用上述方法,你还能得其它的结论吗?DEBD= CE= ∠MDB= ∠∠MEC= ∠点P是 的中点MN⊥ 对称轴所在的直线经过对称点连线段的中点,并且垂直于这条直线结论:线段的垂直平分线经过线段的中点并且垂直于这条线段直线,叫做这条线段的垂直平分线轴对称的性质:1、如果两个图形关于某条直线对称,那么对称轴是任何一对对应点连线段的垂直平分线 2、如果一 个图形是轴对称图形,那么对称轴是任何一对应点连线段的垂直平分线L垂直平分L垂直平分L垂直平分探究三 请同学们动手做一 做木条L与AB钉在一起,L垂直平分AB, 是L上的点,
分别量一量点 到A与B的距离,你有什么发现? 结论:线段垂直平分线上的点与这条线段两个端点的距离相等 ∵L垂直平分AB∴P1A=P1B P2B=P2B
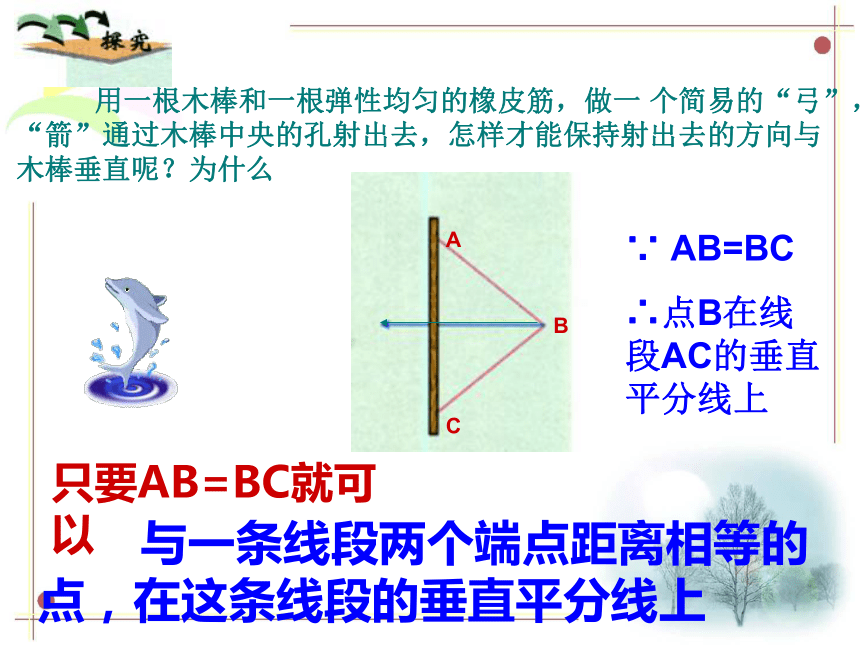
………. 用一根木棒和一根弹性均匀的橡皮筋,做一 个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出去的方向与木棒垂直呢?为什么
CBA只要AB=BC就可以 与一条线段两个端点距离相等的点,在这条线段的垂直平分线上∴点B在线段AC的垂直平分线上∵ AB=BC结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。你能依据例1得到什么结论?定理1 在角的平分线上的点到这个角的两边的距离相等。定理2 到一个角的两边的距离相等的点,在这个角的平分线上。 角的平分线是到角的两边距离相等的所有点的集合 14.1 线段的垂直平分线定 理 线段垂直平分线上的点和这条线段两个端点的距离相等。逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。 线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合ABMNP点的集合是一条射线点的集合是一条直线A′ 如图,EFGH是矩形的台球桌面,有两球分别位于A、B两点的位置,试问怎样撞击A球,才能使A球先碰撞台边EF反弹后再击中B球?试一试:解:1.作点A关于EF的对称点A′ 2.连结A′B交EF于点C则沿AC撞击黑球A,必沿CB反弹击中白球B。C练一练 1、 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE 的长度有什么关系?AB+BD 与DE有什么关系?AB=AC=CEAB+BD=DE2、如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?为什么?∵AB=AC MB=MC∴直线AM垂直平分线段BC(与一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
我的收获小结:1、经过线段的中点并且垂直于这条线段直线,叫做这条线段的垂直平分线3.如何把实际问题抽象或转化为几何模型。2.轴对称的性质:对应点连线段被对称轴垂直平分(1)线段垂直平分线上的点与这条线段连两个端点的距离相等(2)与一条线段两个端点距离相等的点,在这条线段的垂直平分
线上试一试:1、一次晚会上,主持人出了一道题目:“如何把 变成一个真正的等式",很长时间没有人答出,小兰仅仅拿出了一面镜子,就很快解决了这道题目,你知道她是怎样做的吗?再见!授课人:沈海尉2006年11月15日
别是点 A、B、C 的对称点,线段 、 、 与直线MN有什
么关系? 探究一AP=∠MPA=∠ =将△ABC和△ 沿MN折叠
后,点A与点 重合,于是有:探究二1、用上述方法,你还能得其它的结论吗?DEBD= CE= ∠MDB= ∠∠MEC= ∠点P是 的中点MN⊥ 对称轴所在的直线经过对称点连线段的中点,并且垂直于这条直线结论:线段的垂直平分线经过线段的中点并且垂直于这条线段直线,叫做这条线段的垂直平分线轴对称的性质:1、如果两个图形关于某条直线对称,那么对称轴是任何一对对应点连线段的垂直平分线 2、如果一 个图形是轴对称图形,那么对称轴是任何一对应点连线段的垂直平分线L垂直平分L垂直平分L垂直平分探究三 请同学们动手做一 做木条L与AB钉在一起,L垂直平分AB, 是L上的点,
分别量一量点 到A与B的距离,你有什么发现? 结论:线段垂直平分线上的点与这条线段两个端点的距离相等 ∵L垂直平分AB∴P1A=P1B P2B=P2B
………. 用一根木棒和一根弹性均匀的橡皮筋,做一 个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出去的方向与木棒垂直呢?为什么
CBA只要AB=BC就可以 与一条线段两个端点距离相等的点,在这条线段的垂直平分线上∴点B在线段AC的垂直平分线上∵ AB=BC结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。你能依据例1得到什么结论?定理1 在角的平分线上的点到这个角的两边的距离相等。定理2 到一个角的两边的距离相等的点,在这个角的平分线上。 角的平分线是到角的两边距离相等的所有点的集合 14.1 线段的垂直平分线定 理 线段垂直平分线上的点和这条线段两个端点的距离相等。逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。 线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合ABMNP点的集合是一条射线点的集合是一条直线A′ 如图,EFGH是矩形的台球桌面,有两球分别位于A、B两点的位置,试问怎样撞击A球,才能使A球先碰撞台边EF反弹后再击中B球?试一试:解:1.作点A关于EF的对称点A′ 2.连结A′B交EF于点C则沿AC撞击黑球A,必沿CB反弹击中白球B。C练一练 1、 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE 的长度有什么关系?AB+BD 与DE有什么关系?AB=AC=CEAB+BD=DE2、如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?为什么?∵AB=AC MB=MC∴直线AM垂直平分线段BC(与一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
我的收获小结:1、经过线段的中点并且垂直于这条线段直线,叫做这条线段的垂直平分线3.如何把实际问题抽象或转化为几何模型。2.轴对称的性质:对应点连线段被对称轴垂直平分(1)线段垂直平分线上的点与这条线段连两个端点的距离相等(2)与一条线段两个端点距离相等的点,在这条线段的垂直平分
线上试一试:1、一次晚会上,主持人出了一道题目:“如何把 变成一个真正的等式",很长时间没有人答出,小兰仅仅拿出了一面镜子,就很快解决了这道题目,你知道她是怎样做的吗?再见!授课人:沈海尉2006年11月15日
