第十四章 轴对称.doc[上学期]
文档属性
| 名称 | 第十四章 轴对称.doc[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 211.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-01 00:00:00 | ||
图片预览




文档简介
第十四章 轴对称
14.1 轴对称
教学目标
知识技能
1.在生活中认识轴对称,理解轴对称的概念,了解轴对称图形的性质;
2.掌握线段垂直平分线的概念及其性质;
3.掌握作图形轴对称图的方法.
数学思考
1.通过丰富的生活实例认识轴对称,能识别简单的轴对称图形及其对称轴;
2.探究线段垂直平分线的性质,培养学生认真探究、积极思考的能力;
3.在探究过程中,培养学生观察、分析和归纳能力.
情感态度
1.通过对丰富的轴对称现象的认识,进一步培养学生积极的情感、态度,促进观察、分析、归纳、概括等一般能力和审美能力的提高;
2.在探究的过程中,更大程度的激发学生学习的主动性和积极性,并使学生具有一些初步研究问题的能力.
教学重点和难点
重点:
1.轴对称图形的概念以及轴对称的性质;
2.线段垂直平分线的性质.
难点:
1.找出轴对称图形的对称轴;
2.体验轴对称的特征;
3.探索轴对称图形对称轴的作法.
教学过程与流程设计
1.观察图形,认识轴对称图形
把一张纸对折,剪出一个图案(折痕处不要完全剪断),再打开这张对折的纸,就剪出了美丽的窗花.观察得到的窗花,你能发现什么共同的特点?
轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫过轴对称图形,这条直线就是它的对称轴.
课堂练习1:
下列图形是轴对称图形吗?如果是,你能指出它的对称轴吗?
2.观察,认识图形关于轴对称
观察下面的每对图形有什么共同特点?
像上面这样,把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么说这两个图形关于这条折线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.
课堂练习2:
下面给出的每幅图形中的两个图案是轴对称的吗?如果是,使者找出它们的对称轴,并找出一对对称点.
3.自己动手,小组合作,探究两个图形对称的性质,学习垂直平分线的定义
如图,△ABC和△A′B′C′关于直线MN对称,点A′、B′、C′分别是点A、B、C的对称点,线段A A′、B B′、CC′与直线MN有什么关系? 简单证明你的结论.
对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.
垂直平分线:经过线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
思考:(1)线段是轴对称图形吗?如果是,找出它的对称轴;如果不是,说明理由.
(2)如果两个图形关于某条直线对称,则对称轴是任何一对对应点连线的_____.轴对称图形的对称轴是任何一对对应点所连线段的_________ .
4.自主探究垂直平分线的性质
在一张半透明的纸上作一条线段AB,将线段AB对折,使A、B重合,画出折痕l,即直线l是线段AB的垂直平分线.在直线l上取点P1,P2,P3,分别量出P1,P2,P3到A与B的距离,你有什么发现?
垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.
课堂练习3:
如图,△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D.BE=6,求△BCE的周长.
再次讨论,探究垂直平分线性质定理的逆定理是否成立?
下图是由一根木棒和一根弹性均匀的橡皮筋做成的一个简易的“弓”,现在要使“箭”从木棒中央的孔射出去,怎样才能保证射出箭的方向与木棒垂直呢?为什么?
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
课堂练习3:
5.从例题学习中,学习线段垂直平分线的作法
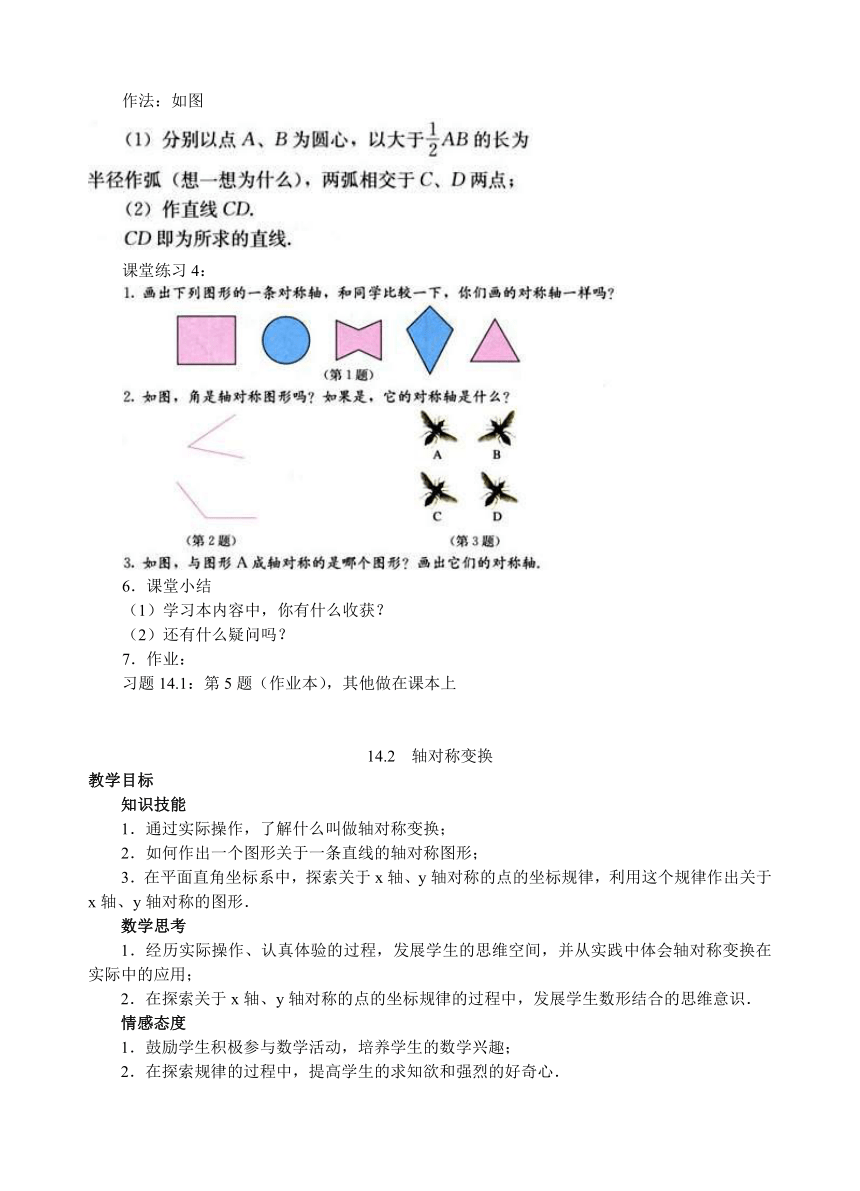
例 如图,点A和点B关于某条直线称轴对称,你能作出这条直线吗?
作法:如图
课堂练习4:
6.课堂小结
(1)学习本内容中,你有什么收获?
(2)还有什么疑问吗?
7.作业:
习题14.1:第5题(作业本),其他做在课本上
14.2 轴对称变换
教学目标
知识技能
1.通过实际操作,了解什么叫做轴对称变换;
2.如何作出一个图形关于一条直线的轴对称图形;
3.在平面直角坐标系中,探索关于x轴、y轴对称的点的坐标规律,利用这个规律作出关于x轴、y轴对称的图形.
数学思考
1.经历实际操作、认真体验的过程,发展学生的思维空间,并从实践中体会轴对称变换在实际中的应用;
2.在探索关于x轴、y轴对称的点的坐标规律的过程中,发展学生数形结合的思维意识.
情感态度
1.鼓励学生积极参与数学活动,培养学生的数学兴趣;
2.在探索规律的过程中,提高学生的求知欲和强烈的好奇心.
教学重点和难点
重点:
1.能够作出简单平面图形的轴对称图形;
2.理解图形上的点的坐标的变化和图形的轴对称变换之间的关系;
3.在用坐标表示轴对称时发展形象思维能力和数形结合的意识.
难点:
1.作出简单平面图形的轴对称图形;
2.用坐标表示轴对称.
教学过程与流程设计
1.自己动手,体会轴对称变换的含义
在一张纸的左边部分,画出一个图形,把这张纸对折后描图,打开对折的纸,可以得到两个图形,这两个图形关于折线对称.连接任意一对对称点的线段被对称轴垂直平分.
类似,可以作出许多美丽的图案.
归纳规律:
像上面这样,有一个平面图形对到它的对称图形叫做轴对称变换.
2.从实践中,探讨如何作出一个图形关于一条直线对称的图形
例 如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
作法:如图
归纳:
课堂练习1:
(1)如图,把下列图形补成关于直线l对称的图形.
(2)用纸片剪一个三角形,分别沿它一边的中线、高、角平分线对折,看看哪些部分能够重合,哪些部分不能重合.
3.探究轴对称的简单应用
如果,要在燃气管道l上修建一个气站,分别向A、B两镇供气.气站修在管道的什么地方,可使所用的输气管线最短?
(学生自主探究完成此问题,要求完成132页的思考题)
4.用坐标表示轴对称
学生任意写出几个点的坐标,在平面直角坐标系中作出这些点的对称点,并求出他们对称点的坐标,总结规律.
规律:
(1)点(x,y)关于x轴对称的点的坐标为(x,-y)
(2)点(x,y)关于y轴对称的点的坐标为(-x,y)
例 四边形ABCD的四个顶点的坐标分别为A(-5,1)、B(-2,1)、C(-2,5)、D(-5,4),分别作出于四边形ABCD关于y轴和x轴对称的图形.
课堂练习2:
5.探究图形关于平行于x轴或y轴的直线对称的规律
如图,分别作出PQR关于直线x=1(记为m)和直线y=-1(几位n)对称的图形.你能发现他们的对应点的坐标之间分别有什么关系吗?
6.课堂小结
(1)学习本内容中,你有什么收获?
(2)还有什么疑问吗?
7.作业
习题14.2 第四题(作业本)其他做在课本
14.3等腰三角形
教学目标:
知识技能
了解等腰三角形的性质,掌握等腰三角形的性质定理及推论,会用定理及推论解决简单问题.
数学思考
培养学生探究思维、逻辑思维能力,探索引辅助线的规律.
情感态度与价值观:
渗透"实践--理论--实践"的辩证唯物主义思想,培养探究分析数学知识方法的兴趣,养成踏实细致、严谨科学的学习习惯.
教学重点与难点
重点:理解等腰三角形的性质定理、推论,并能用它们解决简单的问题.
难点:引辅助线证明定理和推论1的应用.
教学过程与流程设计
引导性材料:
1. 学生把等腰三角形的两腰叠在一起,发现它的两个底角重合,这说明等腰三角形具有什么性质?(等腰三角形的两个底角相等)(演示叠合过程)
2. 教师用等腰三角形纸片演示两腰叠合,再把纸片展开.
提问:你能发现等腰三角形还有什么特性吗
(引入课题,明确目标)(显示教学目标)
教学设计:
问题1:怎样来证明“等腰三角形的两个底角相等”呢?
已知:如图,△ABC中,AB=AC.
求证:∠B=∠C.
(方法1)证明:作顶角的平分线AD.
在△BAD和△CAD中.
AB=AC (已知)
∠1=∠2 (辅助线作法)
AD=AD (公共边)
∴△BAD≌△CAD(SAS)
∴∠B=∠C(全等三角形的对应角相等)
问题2:上述命题还有哪些证法?
方法2:作底边BC上的高AD. (证明过程由学生口述)
方法3:作底边BC上的中线AD.(证明过程由学生口述)
(演示):等腰三角形的性质定理 等腰三角形的两个底角相等
(简写成“等边对等角”)
观察上述三种方法,思考如下问题:
(1) 在等腰△ABC中,如果AD是顶角的平分线,那么AD是否平分底边?是否垂直于底边?
(2) 在等腰△ABC中,如果AD是底边上的高,那么AD是否平分顶角?是否平分底边?
(3) 在等腰△ABC中,如果AD是底边上的中线,那么AD是否平分顶角?是否垂直于底边?
推论1 等腰三角形顶角的平分线平分底边并且垂直于底边.
(等腰三角形的顶角平分线、底边上中线、底边上的高互相重合.)
练习:填空,在△ABC中,
(1) ∵AB=AC,AD⊥BC,
∴∠ =∠ , = .
(2) ∵AB=AC,AD是中线,
∴ ⊥ ,∠ =∠ .
(3) ∵AB=AC,AD是角平分线,
∴ ⊥ , = .
问题2:等边三角形是特殊的等腰三角形,除具有等腰三角形的性质外,还有特殊的性质吗?
推论2:等边三角形的各角都相等,并且每一个角都等于60°.(学生完成证明)
已知:如图,△ABC中,AB=AC=BC.
求证:∠A=∠B=∠C=60°
证明:∵ AB=AC,
∴∠B=∠C(等边对等角),
∵AC=BC,
∴∠A=∠B(等边对等角),
∴∠A=∠B=∠C,
∵∠A+∠B+∠C=180°(三角形内角和定理),
∴∠A=∠B=∠C=60°
例题解析:
例1:填空,1.在△ABC中,AB=AC.
(1) 若∠A=50°,则∠B= °,∠C= °;
(2) 若∠B=45°,则∠A= °,∠C= °;
(3) 若∠B=∠A,则∠A= °,∠C= °;
(4) 若∠B=2∠A,则∠A= °,∠C= °.
2.等腰三角形的一个角是40°,则它的底角是 .
3.等腰三角形的一个角是120°,则它的底角是 .
例2:已知,如图(6),房顶的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC,求顶架上∠B、∠C、∠BAD、∠CAD的度数.
解:在△ABC中,
∵AB=AC(已知),
∴∠B=∠C (等底对等角),
∴∠B=∠C=(180°-∠BAC)=40°,
(三角形内角和定理),
又∵AD⊥BC(已知),
∴∠BAD=∠CAD(等腰三角形顶角的平分线与底边上的高互相重合),
∵∠BAC=100°,
(7) ∴
课堂练习:
已知:如图(7)中的三角形测平架中,AB=AC,在BC的中点挂一个重锤,自然下垂,调整架身,使点恰好在重锤线上.
求证:(1)AD⊥BC;
(2)这时BC处于水平位置,为什么?
课堂小结:
1. 等腰三角形的性质定理:“等边对等角”,揭示了同一个三角形中边与角之间的关系;
2. 等腰三角形性质定理的推论1、推论2;
3. 由推论1知,等腰三角形“底边上的三条主要线段互相重合”,这条线段具有三种不同的“身份”,因此,它是推证两条线段相等、角相等以及两条直线互相垂直必须关注的“热线”.
4. 掌握证明几何命题的完整过程,以及不同辅助线的添法,从中体验数学知识的美妙.
作业:习题14.3 第6、7题(作业本),其他课本
A
B
C
A ′
B ′
C ′
M
N
P
14.1 轴对称
教学目标
知识技能
1.在生活中认识轴对称,理解轴对称的概念,了解轴对称图形的性质;
2.掌握线段垂直平分线的概念及其性质;
3.掌握作图形轴对称图的方法.
数学思考
1.通过丰富的生活实例认识轴对称,能识别简单的轴对称图形及其对称轴;
2.探究线段垂直平分线的性质,培养学生认真探究、积极思考的能力;
3.在探究过程中,培养学生观察、分析和归纳能力.
情感态度
1.通过对丰富的轴对称现象的认识,进一步培养学生积极的情感、态度,促进观察、分析、归纳、概括等一般能力和审美能力的提高;
2.在探究的过程中,更大程度的激发学生学习的主动性和积极性,并使学生具有一些初步研究问题的能力.
教学重点和难点
重点:
1.轴对称图形的概念以及轴对称的性质;
2.线段垂直平分线的性质.
难点:
1.找出轴对称图形的对称轴;
2.体验轴对称的特征;
3.探索轴对称图形对称轴的作法.
教学过程与流程设计
1.观察图形,认识轴对称图形
把一张纸对折,剪出一个图案(折痕处不要完全剪断),再打开这张对折的纸,就剪出了美丽的窗花.观察得到的窗花,你能发现什么共同的特点?
轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫过轴对称图形,这条直线就是它的对称轴.
课堂练习1:
下列图形是轴对称图形吗?如果是,你能指出它的对称轴吗?
2.观察,认识图形关于轴对称
观察下面的每对图形有什么共同特点?
像上面这样,把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么说这两个图形关于这条折线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.
课堂练习2:
下面给出的每幅图形中的两个图案是轴对称的吗?如果是,使者找出它们的对称轴,并找出一对对称点.
3.自己动手,小组合作,探究两个图形对称的性质,学习垂直平分线的定义
如图,△ABC和△A′B′C′关于直线MN对称,点A′、B′、C′分别是点A、B、C的对称点,线段A A′、B B′、CC′与直线MN有什么关系? 简单证明你的结论.
对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.
垂直平分线:经过线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
思考:(1)线段是轴对称图形吗?如果是,找出它的对称轴;如果不是,说明理由.
(2)如果两个图形关于某条直线对称,则对称轴是任何一对对应点连线的_____.轴对称图形的对称轴是任何一对对应点所连线段的_________ .
4.自主探究垂直平分线的性质
在一张半透明的纸上作一条线段AB,将线段AB对折,使A、B重合,画出折痕l,即直线l是线段AB的垂直平分线.在直线l上取点P1,P2,P3,分别量出P1,P2,P3到A与B的距离,你有什么发现?
垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.
课堂练习3:
如图,△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D.BE=6,求△BCE的周长.
再次讨论,探究垂直平分线性质定理的逆定理是否成立?
下图是由一根木棒和一根弹性均匀的橡皮筋做成的一个简易的“弓”,现在要使“箭”从木棒中央的孔射出去,怎样才能保证射出箭的方向与木棒垂直呢?为什么?
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
课堂练习3:
5.从例题学习中,学习线段垂直平分线的作法
例 如图,点A和点B关于某条直线称轴对称,你能作出这条直线吗?
作法:如图
课堂练习4:
6.课堂小结
(1)学习本内容中,你有什么收获?
(2)还有什么疑问吗?
7.作业:
习题14.1:第5题(作业本),其他做在课本上
14.2 轴对称变换
教学目标
知识技能
1.通过实际操作,了解什么叫做轴对称变换;
2.如何作出一个图形关于一条直线的轴对称图形;
3.在平面直角坐标系中,探索关于x轴、y轴对称的点的坐标规律,利用这个规律作出关于x轴、y轴对称的图形.
数学思考
1.经历实际操作、认真体验的过程,发展学生的思维空间,并从实践中体会轴对称变换在实际中的应用;
2.在探索关于x轴、y轴对称的点的坐标规律的过程中,发展学生数形结合的思维意识.
情感态度
1.鼓励学生积极参与数学活动,培养学生的数学兴趣;
2.在探索规律的过程中,提高学生的求知欲和强烈的好奇心.
教学重点和难点
重点:
1.能够作出简单平面图形的轴对称图形;
2.理解图形上的点的坐标的变化和图形的轴对称变换之间的关系;
3.在用坐标表示轴对称时发展形象思维能力和数形结合的意识.
难点:
1.作出简单平面图形的轴对称图形;
2.用坐标表示轴对称.
教学过程与流程设计
1.自己动手,体会轴对称变换的含义
在一张纸的左边部分,画出一个图形,把这张纸对折后描图,打开对折的纸,可以得到两个图形,这两个图形关于折线对称.连接任意一对对称点的线段被对称轴垂直平分.
类似,可以作出许多美丽的图案.
归纳规律:
像上面这样,有一个平面图形对到它的对称图形叫做轴对称变换.
2.从实践中,探讨如何作出一个图形关于一条直线对称的图形
例 如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
作法:如图
归纳:
课堂练习1:
(1)如图,把下列图形补成关于直线l对称的图形.
(2)用纸片剪一个三角形,分别沿它一边的中线、高、角平分线对折,看看哪些部分能够重合,哪些部分不能重合.
3.探究轴对称的简单应用
如果,要在燃气管道l上修建一个气站,分别向A、B两镇供气.气站修在管道的什么地方,可使所用的输气管线最短?
(学生自主探究完成此问题,要求完成132页的思考题)
4.用坐标表示轴对称
学生任意写出几个点的坐标,在平面直角坐标系中作出这些点的对称点,并求出他们对称点的坐标,总结规律.
规律:
(1)点(x,y)关于x轴对称的点的坐标为(x,-y)
(2)点(x,y)关于y轴对称的点的坐标为(-x,y)
例 四边形ABCD的四个顶点的坐标分别为A(-5,1)、B(-2,1)、C(-2,5)、D(-5,4),分别作出于四边形ABCD关于y轴和x轴对称的图形.
课堂练习2:
5.探究图形关于平行于x轴或y轴的直线对称的规律
如图,分别作出PQR关于直线x=1(记为m)和直线y=-1(几位n)对称的图形.你能发现他们的对应点的坐标之间分别有什么关系吗?
6.课堂小结
(1)学习本内容中,你有什么收获?
(2)还有什么疑问吗?
7.作业
习题14.2 第四题(作业本)其他做在课本
14.3等腰三角形
教学目标:
知识技能
了解等腰三角形的性质,掌握等腰三角形的性质定理及推论,会用定理及推论解决简单问题.
数学思考
培养学生探究思维、逻辑思维能力,探索引辅助线的规律.
情感态度与价值观:
渗透"实践--理论--实践"的辩证唯物主义思想,培养探究分析数学知识方法的兴趣,养成踏实细致、严谨科学的学习习惯.
教学重点与难点
重点:理解等腰三角形的性质定理、推论,并能用它们解决简单的问题.
难点:引辅助线证明定理和推论1的应用.
教学过程与流程设计
引导性材料:
1. 学生把等腰三角形的两腰叠在一起,发现它的两个底角重合,这说明等腰三角形具有什么性质?(等腰三角形的两个底角相等)(演示叠合过程)
2. 教师用等腰三角形纸片演示两腰叠合,再把纸片展开.
提问:你能发现等腰三角形还有什么特性吗
(引入课题,明确目标)(显示教学目标)
教学设计:
问题1:怎样来证明“等腰三角形的两个底角相等”呢?
已知:如图,△ABC中,AB=AC.
求证:∠B=∠C.
(方法1)证明:作顶角的平分线AD.
在△BAD和△CAD中.
AB=AC (已知)
∠1=∠2 (辅助线作法)
AD=AD (公共边)
∴△BAD≌△CAD(SAS)
∴∠B=∠C(全等三角形的对应角相等)
问题2:上述命题还有哪些证法?
方法2:作底边BC上的高AD. (证明过程由学生口述)
方法3:作底边BC上的中线AD.(证明过程由学生口述)
(演示):等腰三角形的性质定理 等腰三角形的两个底角相等
(简写成“等边对等角”)
观察上述三种方法,思考如下问题:
(1) 在等腰△ABC中,如果AD是顶角的平分线,那么AD是否平分底边?是否垂直于底边?
(2) 在等腰△ABC中,如果AD是底边上的高,那么AD是否平分顶角?是否平分底边?
(3) 在等腰△ABC中,如果AD是底边上的中线,那么AD是否平分顶角?是否垂直于底边?
推论1 等腰三角形顶角的平分线平分底边并且垂直于底边.
(等腰三角形的顶角平分线、底边上中线、底边上的高互相重合.)
练习:填空,在△ABC中,
(1) ∵AB=AC,AD⊥BC,
∴∠ =∠ , = .
(2) ∵AB=AC,AD是中线,
∴ ⊥ ,∠ =∠ .
(3) ∵AB=AC,AD是角平分线,
∴ ⊥ , = .
问题2:等边三角形是特殊的等腰三角形,除具有等腰三角形的性质外,还有特殊的性质吗?
推论2:等边三角形的各角都相等,并且每一个角都等于60°.(学生完成证明)
已知:如图,△ABC中,AB=AC=BC.
求证:∠A=∠B=∠C=60°
证明:∵ AB=AC,
∴∠B=∠C(等边对等角),
∵AC=BC,
∴∠A=∠B(等边对等角),
∴∠A=∠B=∠C,
∵∠A+∠B+∠C=180°(三角形内角和定理),
∴∠A=∠B=∠C=60°
例题解析:
例1:填空,1.在△ABC中,AB=AC.
(1) 若∠A=50°,则∠B= °,∠C= °;
(2) 若∠B=45°,则∠A= °,∠C= °;
(3) 若∠B=∠A,则∠A= °,∠C= °;
(4) 若∠B=2∠A,则∠A= °,∠C= °.
2.等腰三角形的一个角是40°,则它的底角是 .
3.等腰三角形的一个角是120°,则它的底角是 .
例2:已知,如图(6),房顶的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC,求顶架上∠B、∠C、∠BAD、∠CAD的度数.
解:在△ABC中,
∵AB=AC(已知),
∴∠B=∠C (等底对等角),
∴∠B=∠C=(180°-∠BAC)=40°,
(三角形内角和定理),
又∵AD⊥BC(已知),
∴∠BAD=∠CAD(等腰三角形顶角的平分线与底边上的高互相重合),
∵∠BAC=100°,
(7) ∴
课堂练习:
已知:如图(7)中的三角形测平架中,AB=AC,在BC的中点挂一个重锤,自然下垂,调整架身,使点恰好在重锤线上.
求证:(1)AD⊥BC;
(2)这时BC处于水平位置,为什么?
课堂小结:
1. 等腰三角形的性质定理:“等边对等角”,揭示了同一个三角形中边与角之间的关系;
2. 等腰三角形性质定理的推论1、推论2;
3. 由推论1知,等腰三角形“底边上的三条主要线段互相重合”,这条线段具有三种不同的“身份”,因此,它是推证两条线段相等、角相等以及两条直线互相垂直必须关注的“热线”.
4. 掌握证明几何命题的完整过程,以及不同辅助线的添法,从中体验数学知识的美妙.
作业:习题14.3 第6、7题(作业本),其他课本
A
B
C
A ′
B ′
C ′
M
N
P
