北师大版九年级上册数学 1.1.2菱形的判定 课件(共16张PPT)
文档属性
| 名称 | 北师大版九年级上册数学 1.1.2菱形的判定 课件(共16张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
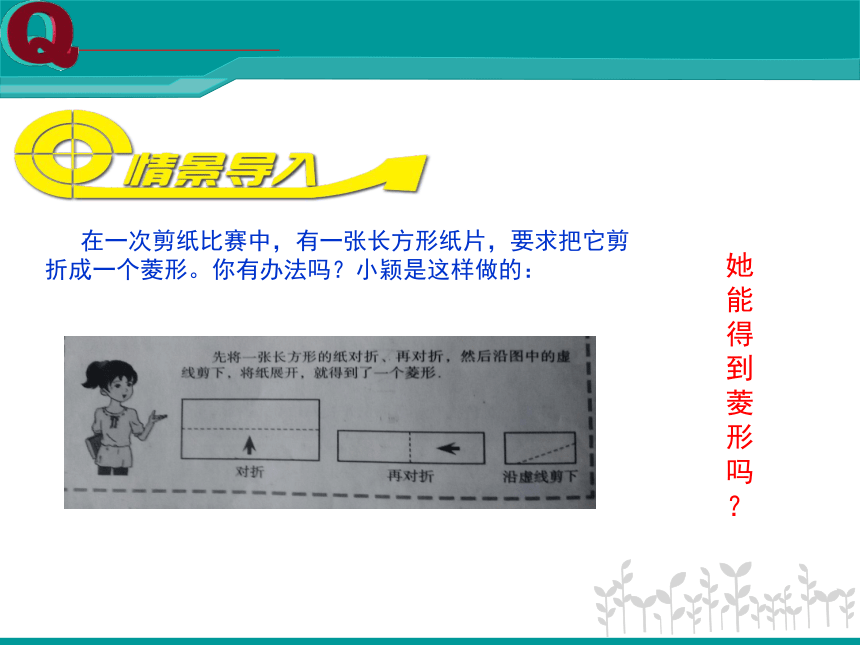
在一次剪纸比赛中,有一张长方形纸片,要求把它剪
折成一个菱形。你有办法吗?小颖是这样做的:
她能得到菱形吗
?
北师大版本九年级数学(上)
第一章 特殊平行四边形
菱形的性质与判定(第2课时)
菱形的判定
学习目标
1.掌握菱形的判定定理及方法,并利用判定方法解决一些问题.
2.经历菱形判定定理的探索过程,进一步发展学生推理 能力.
3.引领学生积极参与数学学习活动,激发学习数学求知欲,提升数学素养.
回顾反馈
1.菱形的定义
2.如图,已知□ABCD,只需补充一个条件就可以判定它是一个菱形.补充的条件是_____.
通过探究,容易得到:
对角线 互相垂直 的平行四边形是菱形
展示交流
活动1: 用一长一短两根木条,在它们的中点处固定一个小钉,做成一个可转动的十字,四周围上橡皮筋,做成一个四边形.转动木条,木条端点围成的四边形是平行四边形吗?什么时候变成菱形?
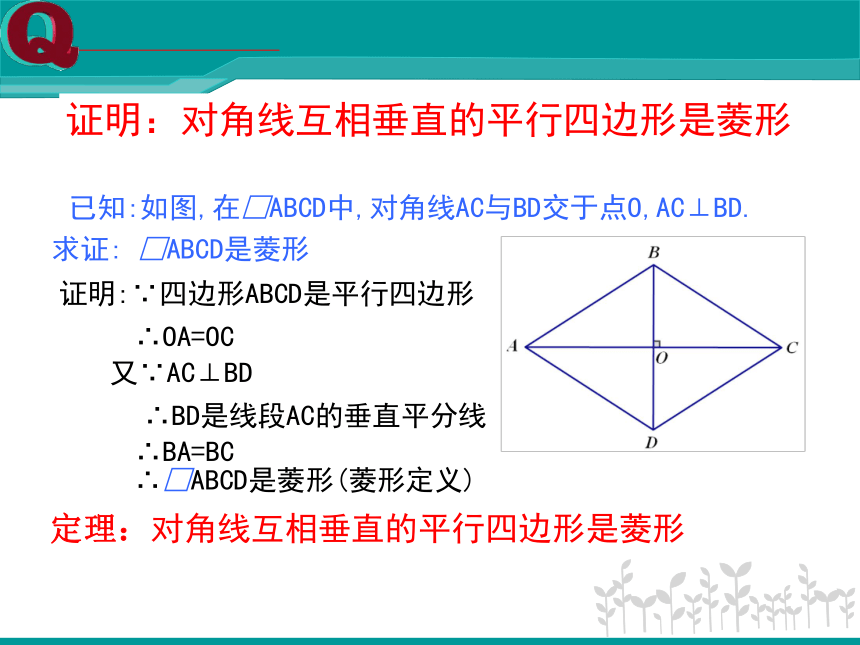
证明:对角线互相垂直的平行四边形是菱形
已知:如图,在□ABCD中,对角线AC与BD交于点O,AC⊥BD.
求证: □ABCD是菱形
证明:∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD
∴BD是线段AC的垂直平分线
∴BA=BC
∴□ABCD是菱形(菱形定义)
定理:对角线互相垂直的平行四边形是菱形
课堂训练一
下列条件中,可以判定一个四边形是菱形的是( )
A.两条对角线相等
B.两条对角线互相垂直
C.两条对角线相等且垂直
D.两条对角线互相垂直平分
D
活动2:已知线段AC,你能用尺规作图的方法做一个菱形ABCD,使AC为菱形的一条对角线吗
A
C
展示交流
已知:如图四边形ABCD中,AB=BC=CD=DA.
求证: 四边形ABCD是菱形
证明:∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=BC
∴四边形ABCD是菱形(菱形定义)
四条边相等的四边形是菱形吗?
定理:四条边相等的四边形是菱形
A
B
C
D
证明:在△AOB中,
∴AB2=OA2+OB2
∴△AOB是直角三角形,∠AOB是直角.
∴AC⊥BD
∴□ABCD是菱形(对角线垂直的平行四边形是菱形)
∵ AB= √5,OA=2,OB=1
D
B
C
A
O
展示交流
活动3:同学们,前面情景导入要求用长
方形纸折出一个菱形,现在请大家操作并交流展示自己的成果。
如图所示,D,E,F分别是△ABC的边BC,CA,AB上的点,且DE∥AB,DF∥CA,要使四边形AFDE是菱形,则要增加的条件是______.(写出符合要求的一个即可)
课堂训练二
如图,□ABCD的对角线AC的垂直平分线与两边 AB、CD的延长线分别相交与E、F.
求证:四边形AECF为菱形。
O
O
拓展提升
菱形的判定方法:
1.有一组邻边相等的平行四边形是菱形;
2.对角线互相垂直的平行四边形是菱形;
3.对角线互相垂直且平分的四边形是菱形;
4.四边相等的四边形是菱形。
我对自己说:
我对同学说:
我对老师说:
祝同学们学习进步,在数学的海洋中扬帆远航!
驶向胜利的彼岸
在一次剪纸比赛中,有一张长方形纸片,要求把它剪
折成一个菱形。你有办法吗?小颖是这样做的:
她能得到菱形吗
?
北师大版本九年级数学(上)
第一章 特殊平行四边形
菱形的性质与判定(第2课时)
菱形的判定
学习目标
1.掌握菱形的判定定理及方法,并利用判定方法解决一些问题.
2.经历菱形判定定理的探索过程,进一步发展学生推理 能力.
3.引领学生积极参与数学学习活动,激发学习数学求知欲,提升数学素养.
回顾反馈
1.菱形的定义
2.如图,已知□ABCD,只需补充一个条件就可以判定它是一个菱形.补充的条件是_____.
通过探究,容易得到:
对角线 互相垂直 的平行四边形是菱形
展示交流
活动1: 用一长一短两根木条,在它们的中点处固定一个小钉,做成一个可转动的十字,四周围上橡皮筋,做成一个四边形.转动木条,木条端点围成的四边形是平行四边形吗?什么时候变成菱形?
证明:对角线互相垂直的平行四边形是菱形
已知:如图,在□ABCD中,对角线AC与BD交于点O,AC⊥BD.
求证: □ABCD是菱形
证明:∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD
∴BD是线段AC的垂直平分线
∴BA=BC
∴□ABCD是菱形(菱形定义)
定理:对角线互相垂直的平行四边形是菱形
课堂训练一
下列条件中,可以判定一个四边形是菱形的是( )
A.两条对角线相等
B.两条对角线互相垂直
C.两条对角线相等且垂直
D.两条对角线互相垂直平分
D
活动2:已知线段AC,你能用尺规作图的方法做一个菱形ABCD,使AC为菱形的一条对角线吗
A
C
展示交流
已知:如图四边形ABCD中,AB=BC=CD=DA.
求证: 四边形ABCD是菱形
证明:∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=BC
∴四边形ABCD是菱形(菱形定义)
四条边相等的四边形是菱形吗?
定理:四条边相等的四边形是菱形
A
B
C
D
证明:在△AOB中,
∴AB2=OA2+OB2
∴△AOB是直角三角形,∠AOB是直角.
∴AC⊥BD
∴□ABCD是菱形(对角线垂直的平行四边形是菱形)
∵ AB= √5,OA=2,OB=1
D
B
C
A
O
展示交流
活动3:同学们,前面情景导入要求用长
方形纸折出一个菱形,现在请大家操作并交流展示自己的成果。
如图所示,D,E,F分别是△ABC的边BC,CA,AB上的点,且DE∥AB,DF∥CA,要使四边形AFDE是菱形,则要增加的条件是______.(写出符合要求的一个即可)
课堂训练二
如图,□ABCD的对角线AC的垂直平分线与两边 AB、CD的延长线分别相交与E、F.
求证:四边形AECF为菱形。
O
O
拓展提升
菱形的判定方法:
1.有一组邻边相等的平行四边形是菱形;
2.对角线互相垂直的平行四边形是菱形;
3.对角线互相垂直且平分的四边形是菱形;
4.四边相等的四边形是菱形。
我对自己说:
我对同学说:
我对老师说:
祝同学们学习进步,在数学的海洋中扬帆远航!
驶向胜利的彼岸
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
