北师大版九年级上册数学 1.2.2矩形的判定 课件(共21张PPT)
文档属性
| 名称 | 北师大版九年级上册数学 1.2.2矩形的判定 课件(共21张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 460.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 15:20:18 | ||
图片预览







文档简介
(共21张PPT)
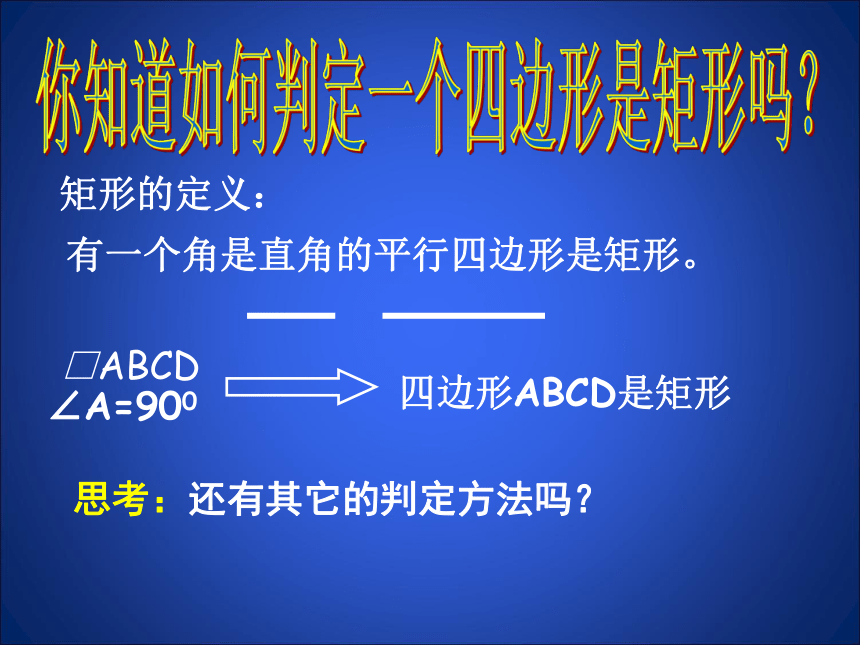
定义:有一个角是直角的平行四边形叫做矩形。
矩形性质 角 边 对角线 对称性
推论:直角三角形斜边上的中线等于斜边的一半。
A
C
B
D
复习与回顾
四个角都是直角
对边平行
且相等
互相平分
且相等
既是轴对称图形,又是中心对称图形
矩形的定义:
有一个角是直角的平行四边形是矩形。
∠A=900
四边形ABCD是矩形
□ABCD
思考:还有其它的判定方法吗?
第一章 特殊平行四边形
第2节 矩形的性质与判定(二)
学习目标
1.理解并会证明矩形的判定定理;
2.能运用矩形的判定定理解决实际问题。
学习指导
认真阅读教材14--15页的内容:
1.思考“做一做” 中提出的问题。
你能得到关于矩形的判定定理吗?
它的内容是什么?怎样证明?
2.思考“想一想”的内容,你认为矩形
还有哪些判定定理,为什么?
3.自学例2,如有疑问与同伴交流。
5分钟后回答老师提出的问题
情境一
如图,在一个平行四边形活动框架上,用两根橡皮筋分别套在两个相对的顶点上,拉动一对不相邻的顶点时,平行四边形的形状会发生什么变化?
问题(2):当两条对角线的长度相等时平行四边形有什么特征?由此你能得到一个怎样的猜想?
问题(1):随着 的变化,两条对角线的长度发生怎样的变化?
四边形ABCD是平行四边形,AC=BD.
四边形ABCD是矩形.
已知:
求证:
猜想:对角线相等的平行四边形是矩形。
A
B
C
D
证明:∵AB = DC,BC = CB,
AC = DB,
∴ △ABC≌△DCB ,
∴∠ABC = ∠DCB。
∵AB∥CD,
∴∠ABC + ∠DCB = 180°,
∴ ∠ABC = 90°,
∴ ABCD是矩形。
ABCD
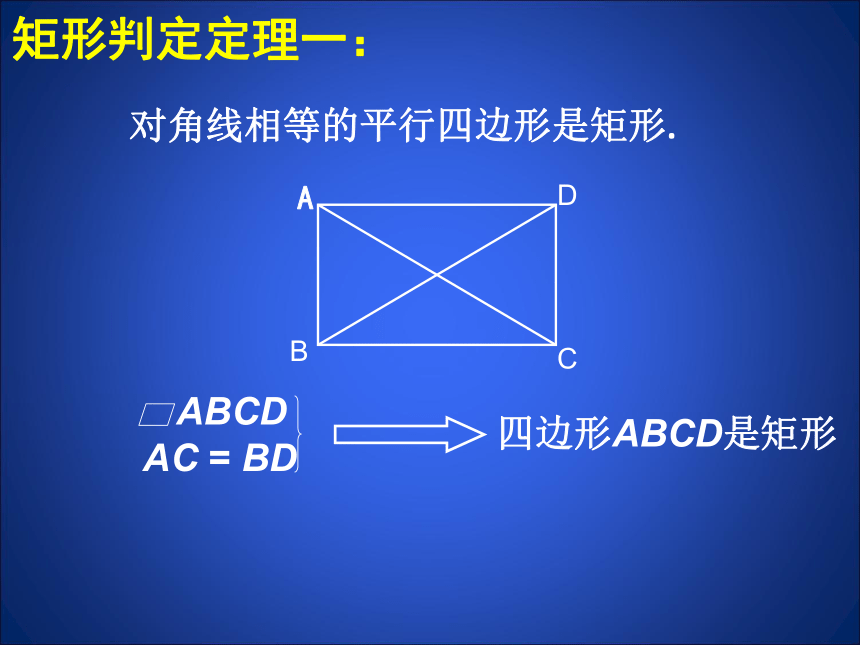
AC = BD
四边形ABCD是矩形
矩形判定定理一:
对角线相等的平行四边形是矩形.
A
B
C
D
1下列命题是否正确?
(1)对角线相等的四边形是矩形.( )
(2)对角线互相平分且相等的四边形是矩形.( )
(3)对角线相等,且有一个角是直角的四边形是矩形. ( )
X
X
√
跟踪训练
议一议:工人师傅想检验四边形窗框是否成矩形,但手里仅仅有一根较长的绳子,则他能否检测出窗框是不是矩形呢?他怎么做呢?
原理:对角线相等的平行四边形是矩形 。
情境二
李芳同学用四步画出了一个四边形,她的画法是“边——直角、边——直角、边——直角、边” ,她说这就是一个矩形,她的判断对吗?为什么?
猜想:
你能证明上述结论吗?
有三个角是直角的四边形是矩形.
猜想:有三个角是直角的四边形是矩形。
证明:
∵∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
已知:如图,在四边形ABCD,∠A=∠B=∠C=90°.
D
B
C
A
∴四边形ABCD是矩形.
∵∠C=90°,
有三个角是直角的四边形是矩形
∠A=∠B=∠C=90°
四边形ABCD
是矩形
D
B
C
A
矩形判定定理二
能够判断一个四边形是矩形的条件是
A.对角线相等 B.对角线垂直
C.四个角都相等 D.对角线垂直且相等
选择题
[ ]
C
课堂练习
判定一个四边形是矩形的方法与思路是:
1.如图所示,已知□ABCD,下列条件:①AC=BD;②AB=AD;③∠1=∠2;④AB⊥BC中,能说明□ABCD是矩形的有 (填写序号).
【解析】根据对角线相等的平行四边形是矩形;矩形的定义.
答案:① ③ ④
A
D
B
C
O
)
1
2(
达标检测1
达标检测 2
已知:如图,在△ABC中,∠ACB=90°,CD为中线,延长CD到点E,使得 DE=CD。连结AE,BE,求证:四边形ACBE为矩形。
A
B
C
D
E
已知:如图,菱形ABCD中,对角线AC和BD相较于点O,CM∥BD,DM∥AC.
求证:四边形OCMD是矩形.
达标检测 3
A
B
C
D
O
M
∠A= ∠B= ∠C=90°
ABCD
AC = BD
ABCD
∠A=90°
ABCD
是矩形
四边形ABCD
是矩形
谈一谈,今天你有何收获?
定义:有一个角是直角的平行四边形叫做矩形。
矩形性质 角 边 对角线 对称性
推论:直角三角形斜边上的中线等于斜边的一半。
A
C
B
D
复习与回顾
四个角都是直角
对边平行
且相等
互相平分
且相等
既是轴对称图形,又是中心对称图形
矩形的定义:
有一个角是直角的平行四边形是矩形。
∠A=900
四边形ABCD是矩形
□ABCD
思考:还有其它的判定方法吗?
第一章 特殊平行四边形
第2节 矩形的性质与判定(二)
学习目标
1.理解并会证明矩形的判定定理;
2.能运用矩形的判定定理解决实际问题。
学习指导
认真阅读教材14--15页的内容:
1.思考“做一做” 中提出的问题。
你能得到关于矩形的判定定理吗?
它的内容是什么?怎样证明?
2.思考“想一想”的内容,你认为矩形
还有哪些判定定理,为什么?
3.自学例2,如有疑问与同伴交流。
5分钟后回答老师提出的问题
情境一
如图,在一个平行四边形活动框架上,用两根橡皮筋分别套在两个相对的顶点上,拉动一对不相邻的顶点时,平行四边形的形状会发生什么变化?
问题(2):当两条对角线的长度相等时平行四边形有什么特征?由此你能得到一个怎样的猜想?
问题(1):随着 的变化,两条对角线的长度发生怎样的变化?
四边形ABCD是平行四边形,AC=BD.
四边形ABCD是矩形.
已知:
求证:
猜想:对角线相等的平行四边形是矩形。
A
B
C
D
证明:∵AB = DC,BC = CB,
AC = DB,
∴ △ABC≌△DCB ,
∴∠ABC = ∠DCB。
∵AB∥CD,
∴∠ABC + ∠DCB = 180°,
∴ ∠ABC = 90°,
∴ ABCD是矩形。
ABCD
AC = BD
四边形ABCD是矩形
矩形判定定理一:
对角线相等的平行四边形是矩形.
A
B
C
D
1下列命题是否正确?
(1)对角线相等的四边形是矩形.( )
(2)对角线互相平分且相等的四边形是矩形.( )
(3)对角线相等,且有一个角是直角的四边形是矩形. ( )
X
X
√
跟踪训练
议一议:工人师傅想检验四边形窗框是否成矩形,但手里仅仅有一根较长的绳子,则他能否检测出窗框是不是矩形呢?他怎么做呢?
原理:对角线相等的平行四边形是矩形 。
情境二
李芳同学用四步画出了一个四边形,她的画法是“边——直角、边——直角、边——直角、边” ,她说这就是一个矩形,她的判断对吗?为什么?
猜想:
你能证明上述结论吗?
有三个角是直角的四边形是矩形.
猜想:有三个角是直角的四边形是矩形。
证明:
∵∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
已知:如图,在四边形ABCD,∠A=∠B=∠C=90°.
D
B
C
A
∴四边形ABCD是矩形.
∵∠C=90°,
有三个角是直角的四边形是矩形
∠A=∠B=∠C=90°
四边形ABCD
是矩形
D
B
C
A
矩形判定定理二
能够判断一个四边形是矩形的条件是
A.对角线相等 B.对角线垂直
C.四个角都相等 D.对角线垂直且相等
选择题
[ ]
C
课堂练习
判定一个四边形是矩形的方法与思路是:
1.如图所示,已知□ABCD,下列条件:①AC=BD;②AB=AD;③∠1=∠2;④AB⊥BC中,能说明□ABCD是矩形的有 (填写序号).
【解析】根据对角线相等的平行四边形是矩形;矩形的定义.
答案:① ③ ④
A
D
B
C
O
)
1
2(
达标检测1
达标检测 2
已知:如图,在△ABC中,∠ACB=90°,CD为中线,延长CD到点E,使得 DE=CD。连结AE,BE,求证:四边形ACBE为矩形。
A
B
C
D
E
已知:如图,菱形ABCD中,对角线AC和BD相较于点O,CM∥BD,DM∥AC.
求证:四边形OCMD是矩形.
达标检测 3
A
B
C
D
O
M
∠A= ∠B= ∠C=90°
ABCD
AC = BD
ABCD
∠A=90°
ABCD
是矩形
四边形ABCD
是矩形
谈一谈,今天你有何收获?
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
