北师大版九年级上册 1.2.3矩形的性质与判定的综合应用 课件(共23张PPT)
文档属性
| 名称 | 北师大版九年级上册 1.2.3矩形的性质与判定的综合应用 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 409.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
2.矩形的性质应用——折叠问题
九年级数学(上)
第一章 特殊平行四边形
矩形还有哪些特殊性质?
矩形有哪些性质?
具有平行四边形的所有性质
边:矩形的对边平行且相等
角:矩形对角相等;邻角互补
对角线:矩形对角线互相平分
矩形的特殊性质
性质1、矩形的四个角都是直角.
性质2、矩形的两条对角线相等.
几何语言:
∵四边形ABCD是矩形
AC = BD
∴∠A=∠B=∠C=∠D=90°
矩形的性质
边的性质:
矩形的对边平行且相等.
角的性质:
矩形的四个角都是直角.
对角线的性质:
矩形的对角线相等,且互相平分.
矩形性质的重要应用
——
折叠问题
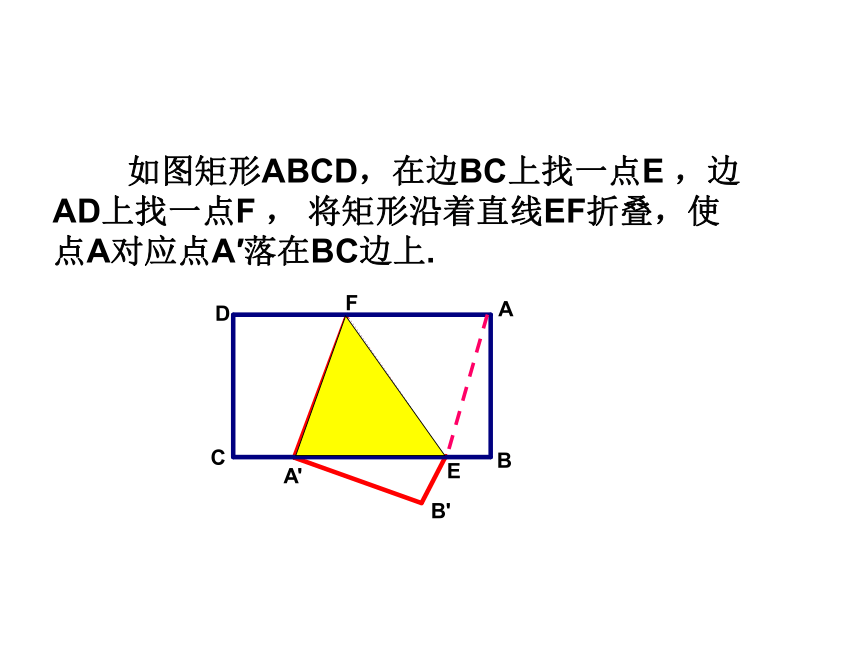
如图矩形ABCD,在边BC上找一点E ,边AD上找一点F , 将矩形沿着直线EF折叠,使点A对应点A′落在BC边上.
图2
图1
图3
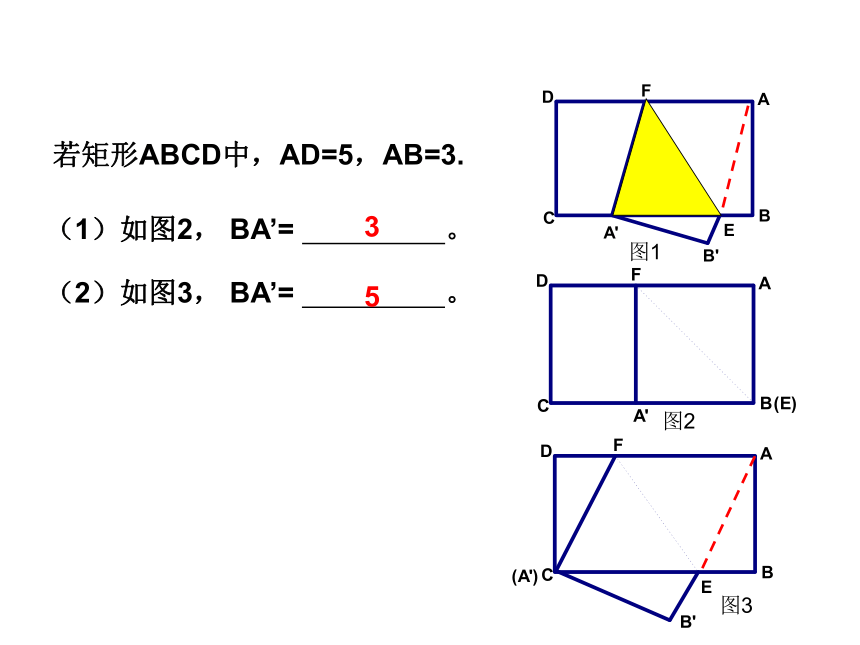
(1)如图2, BA’= 。
若矩形ABCD中,AD=5,AB=3.
3
(2)如图3, BA’= 。
5
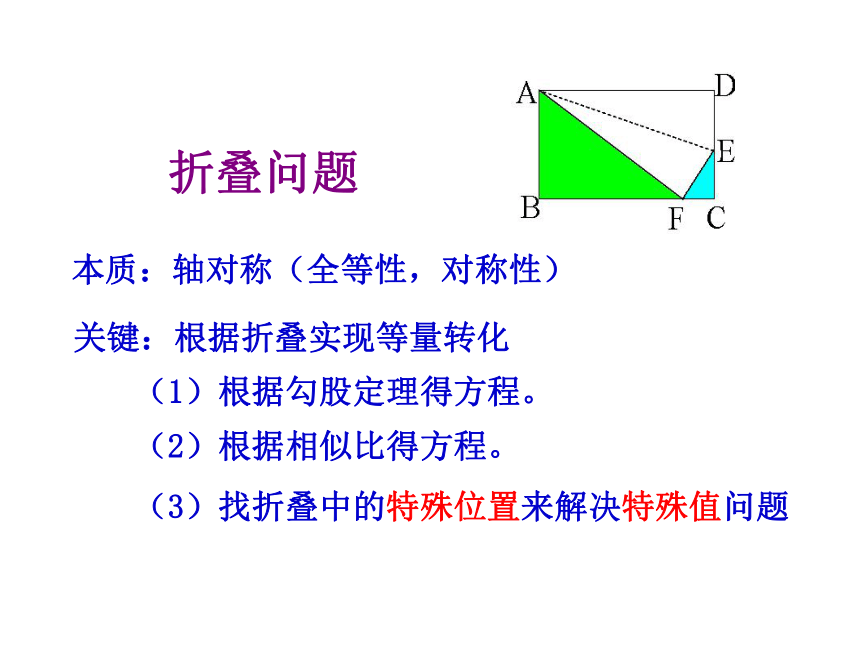
关键:根据折叠实现等量转化
(2)根据相似比得方程。
(1)根据勾股定理得方程。
折叠问题
本质:轴对称(全等性,对称性)
(3)找折叠中的特殊位置来解决特殊值问题
角度的计算
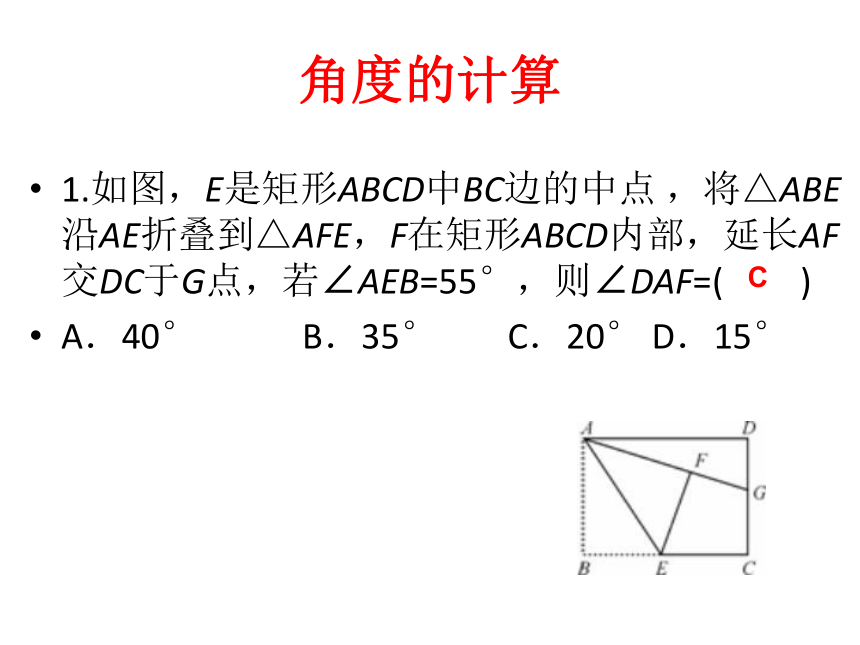
1.如图,E是矩形ABCD中BC边的中点 ,将△ABE沿AE折叠到△AFE,F在矩形ABCD内部,延长AF交DC于G点,若∠AEB=55°,则∠DAF=( )
A.40° B.35° C.20° D.15°
C
2.如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于( )
A.50° B.55° C.60° D.65°
A
边长的计算
1.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE长为( )
A.3 B.4 C.5 D.6
C
2.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为( )
A.1 B.2 C. D.
D
1.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
面积的计算
1.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( 16) )
面积的计算
2.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC的面积为( )
10
3、把矩形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处如图),已知∠MPN=90°,PM=3,PN=4,那么矩形纸片ABCD的面积为_________.
28.8
1、感知:如图①,在矩形ABCD中,点E是边BC的中点,将△ABE沿AE折叠,使点B落在矩形ABCD内部的点F处,延长AF交CD于点G,连结FC,易证∠GCF=∠GFC.
探究:将图①中的矩形ABCD改为平行四边形,其他条件不变,如图②,判断∠GCF=∠GFC是否仍然相等,并说明理由.
应用:如图②,若AB=5,BC=6,则△ADG的周长为 .
四、与动点的结合
【解答】解:探究:∠GCF=∠GFC,理由如下:
∵四边形ABCD是平行四边形,∴AB∥CD,∴∠B+∠ECG=180°,
又∵△AFE是由△ABE翻折得到,∴∠AFE=∠B,EF=BE,
又∵∠AFE+∠EFG=180°,∴∠ECG=∠EFG,
又∵点E是边BC的中点,∴EC=BE,
∵EF=BE,∴EC=EF,∴∠ECF=∠EFC,∴∠ECG﹣∠ECF=∠EFG﹣∠EFC,∴∠GCF=∠GFC;
应用:∵△AFE是由△ABE翻折得到,∴AF=AB=5,
由(1)知∠GCF=∠GFC,∴GF=GC,
∴△ADG的周长AD+AF+GF+GD=AD+AB+GC+GD=AD+AB+CD=6+5+5=16,
2.(1)观察与发现:小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);在第一次的折叠基础上第二次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②).小明认为△AEF是等腰三角形,你同意吗?请说明理由.
(2)实践与运用:将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点D′处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中∠α的大小.
【解答】解:(1)同意.如图,设AD与EF交于点G.由折叠知,AD平分∠BAC,所以∠BAD=∠CAD.
又由折叠知,∠AGE=∠DGE,∠AGE+∠DGE=180°,所以∠AGE=∠AGF=90°,所以∠AEF=∠AFE.所以AE=AF,
即△AEF为等腰三角形.
(2)由折叠知,四边形ABFE是正方形,∠AEB=45°,所以∠BED=135度.
又由折叠知,∠BEG=∠DEG,所以∠DEG=67.5度.从而∠α=67.5°﹣45°=22.5°.
课堂小结
矩形的性质
折叠问题的解决
关键:根据折叠实现等量转化
(2)根据相似比得方程。
(1)根据勾股定理得方程。
折叠问题
本质:轴对称(全等性,对称性)
(3)找折叠中的特殊位置来解决特殊值问题
谢谢大家
2.矩形的性质应用——折叠问题
九年级数学(上)
第一章 特殊平行四边形
矩形还有哪些特殊性质?
矩形有哪些性质?
具有平行四边形的所有性质
边:矩形的对边平行且相等
角:矩形对角相等;邻角互补
对角线:矩形对角线互相平分
矩形的特殊性质
性质1、矩形的四个角都是直角.
性质2、矩形的两条对角线相等.
几何语言:
∵四边形ABCD是矩形
AC = BD
∴∠A=∠B=∠C=∠D=90°
矩形的性质
边的性质:
矩形的对边平行且相等.
角的性质:
矩形的四个角都是直角.
对角线的性质:
矩形的对角线相等,且互相平分.
矩形性质的重要应用
——
折叠问题
如图矩形ABCD,在边BC上找一点E ,边AD上找一点F , 将矩形沿着直线EF折叠,使点A对应点A′落在BC边上.
图2
图1
图3
(1)如图2, BA’= 。
若矩形ABCD中,AD=5,AB=3.
3
(2)如图3, BA’= 。
5
关键:根据折叠实现等量转化
(2)根据相似比得方程。
(1)根据勾股定理得方程。
折叠问题
本质:轴对称(全等性,对称性)
(3)找折叠中的特殊位置来解决特殊值问题
角度的计算
1.如图,E是矩形ABCD中BC边的中点 ,将△ABE沿AE折叠到△AFE,F在矩形ABCD内部,延长AF交DC于G点,若∠AEB=55°,则∠DAF=( )
A.40° B.35° C.20° D.15°
C
2.如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于( )
A.50° B.55° C.60° D.65°
A
边长的计算
1.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE长为( )
A.3 B.4 C.5 D.6
C
2.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为( )
A.1 B.2 C. D.
D
1.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
面积的计算
1.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( 16) )
面积的计算
2.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC的面积为( )
10
3、把矩形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处如图),已知∠MPN=90°,PM=3,PN=4,那么矩形纸片ABCD的面积为_________.
28.8
1、感知:如图①,在矩形ABCD中,点E是边BC的中点,将△ABE沿AE折叠,使点B落在矩形ABCD内部的点F处,延长AF交CD于点G,连结FC,易证∠GCF=∠GFC.
探究:将图①中的矩形ABCD改为平行四边形,其他条件不变,如图②,判断∠GCF=∠GFC是否仍然相等,并说明理由.
应用:如图②,若AB=5,BC=6,则△ADG的周长为 .
四、与动点的结合
【解答】解:探究:∠GCF=∠GFC,理由如下:
∵四边形ABCD是平行四边形,∴AB∥CD,∴∠B+∠ECG=180°,
又∵△AFE是由△ABE翻折得到,∴∠AFE=∠B,EF=BE,
又∵∠AFE+∠EFG=180°,∴∠ECG=∠EFG,
又∵点E是边BC的中点,∴EC=BE,
∵EF=BE,∴EC=EF,∴∠ECF=∠EFC,∴∠ECG﹣∠ECF=∠EFG﹣∠EFC,∴∠GCF=∠GFC;
应用:∵△AFE是由△ABE翻折得到,∴AF=AB=5,
由(1)知∠GCF=∠GFC,∴GF=GC,
∴△ADG的周长AD+AF+GF+GD=AD+AB+GC+GD=AD+AB+CD=6+5+5=16,
2.(1)观察与发现:小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);在第一次的折叠基础上第二次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②).小明认为△AEF是等腰三角形,你同意吗?请说明理由.
(2)实践与运用:将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点D′处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中∠α的大小.
【解答】解:(1)同意.如图,设AD与EF交于点G.由折叠知,AD平分∠BAC,所以∠BAD=∠CAD.
又由折叠知,∠AGE=∠DGE,∠AGE+∠DGE=180°,所以∠AGE=∠AGF=90°,所以∠AEF=∠AFE.所以AE=AF,
即△AEF为等腰三角形.
(2)由折叠知,四边形ABFE是正方形,∠AEB=45°,所以∠BED=135度.
又由折叠知,∠BEG=∠DEG,所以∠DEG=67.5度.从而∠α=67.5°﹣45°=22.5°.
课堂小结
矩形的性质
折叠问题的解决
关键:根据折叠实现等量转化
(2)根据相似比得方程。
(1)根据勾股定理得方程。
折叠问题
本质:轴对称(全等性,对称性)
(3)找折叠中的特殊位置来解决特殊值问题
谢谢大家
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
