北师大版九年级上册数学 1.3.2正方形的判定 课件(共25张PPT)
文档属性
| 名称 | 北师大版九年级上册数学 1.3.2正方形的判定 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
1.3.2 正方形的判定
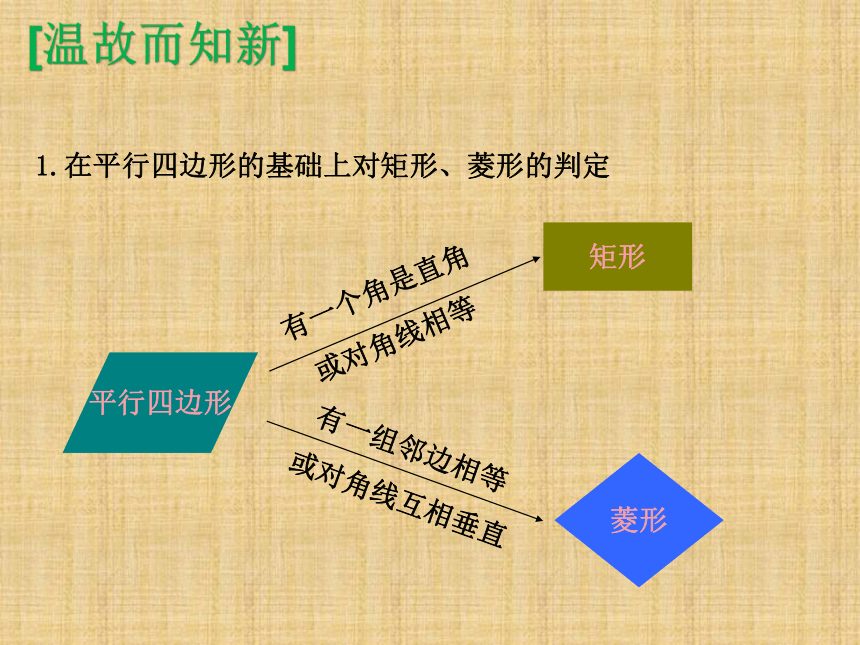
1.在平行四边形的基础上对矩形、菱形的判定
[温故而知新]
有一个角是直角
或对角线相等
平行四边形
矩形
菱形
有一组邻边相等
或对角线互相垂直
一个角是直角
有一个角是直角且一组邻边相等的平行四边形叫做正方形
正方形的两条对角线互相垂直平分且相等,
每条对角线平分一组对角
正方形的对边平行且相等
正方形的四个角都是直角
边
对角线
角
2.正方形的定义及性质
正方形的性质
且一组邻边相等
[温故而知新]
平行四边形
正方形
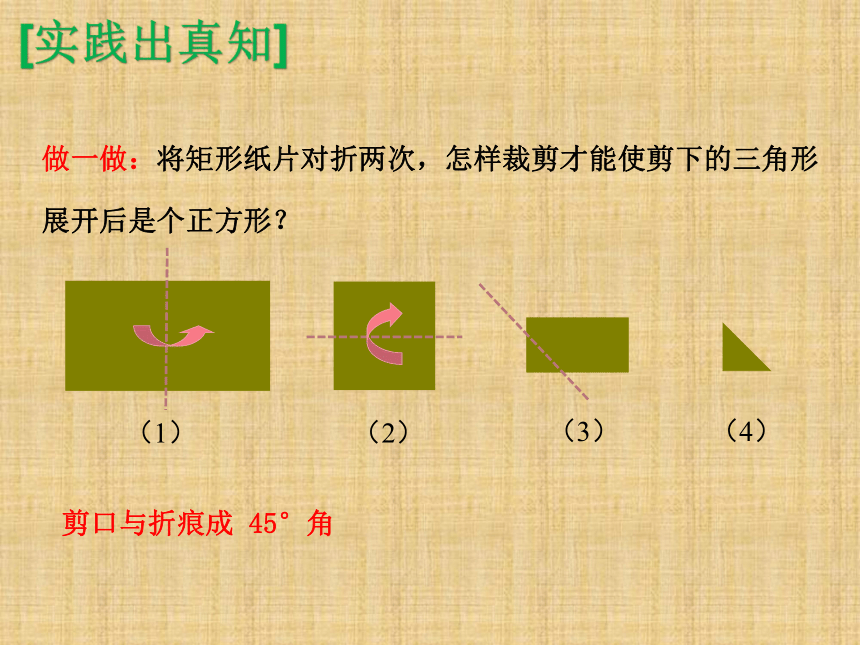
做一做:将矩形纸片对折两次,怎样裁剪才能使剪下的三角形
展开后是个正方形?
(1)
(2)
(3)
(4)
剪口与折痕成 45°角
菱形
问题2:满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
或对角线互相垂直
问题3:满足怎样条件的菱形是正方形?
一个角是直角
或对角线相等
正方形
1.有一组邻边相等的矩形是正方形.
2.对角线互相垂直的矩形是正方形.
3.有一个角是直角的菱形是正方形.
4.对角线相等的菱形是正方形.
定理
[实践出真知]
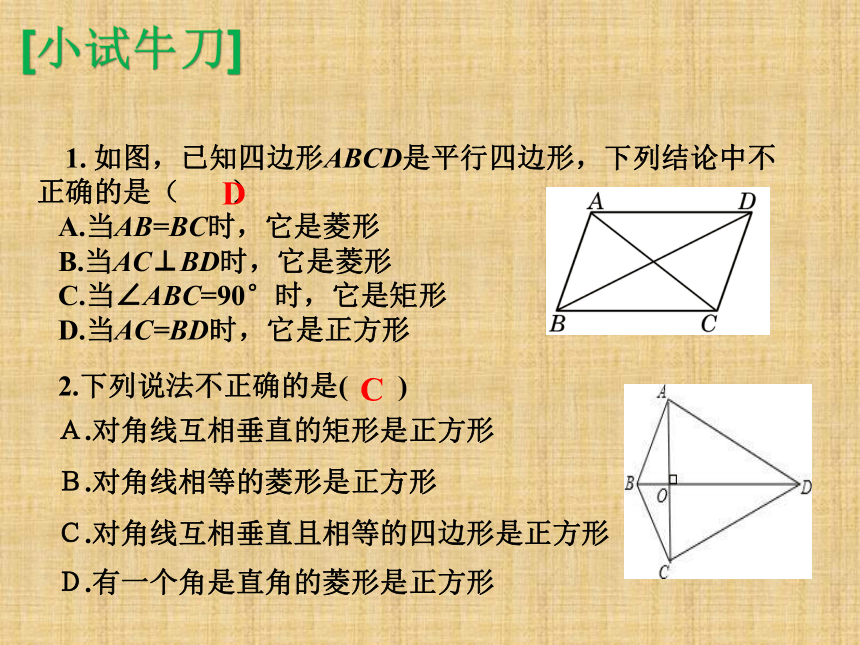
[小试牛刀]
1. 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
D
2.下列说法不正确的是( )
A.对角线互相垂直的矩形是正方形
B.对角线相等的菱形是正方形
C.对角线互相垂直且相等的四边形是正方形
D.有一个角是直角的菱形是正方形
C
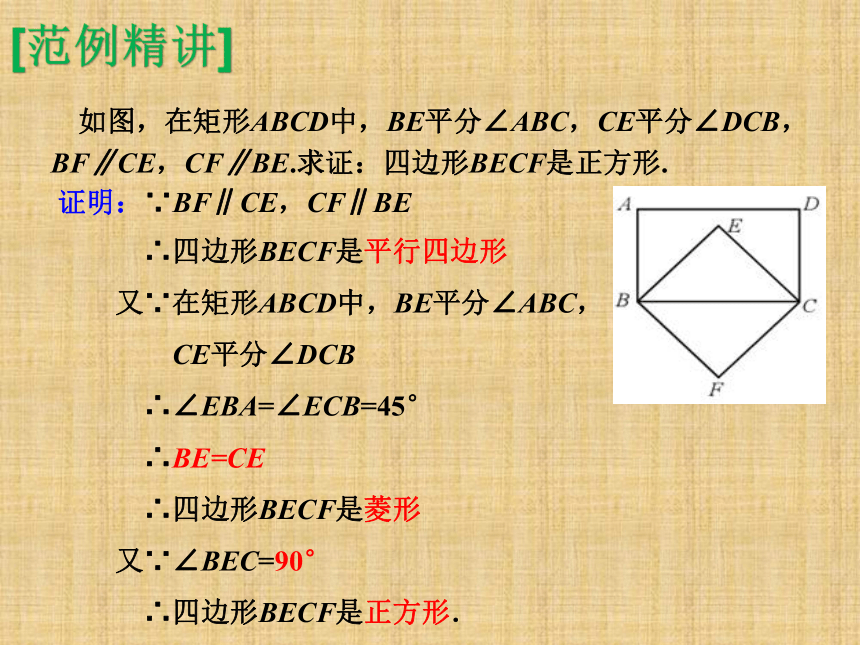
证明:∵BF∥CE,CF∥BE
∴四边形BECF是平行四边形
又∵在矩形ABCD中,BE平分∠ABC,
CE平分∠DCB
∴∠EBA=∠ECB=45°
∴BE=CE
∴四边形BECF是菱形
又∵∠BEC=90°
∴四边形BECF是正方形.
如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
[范例精讲]
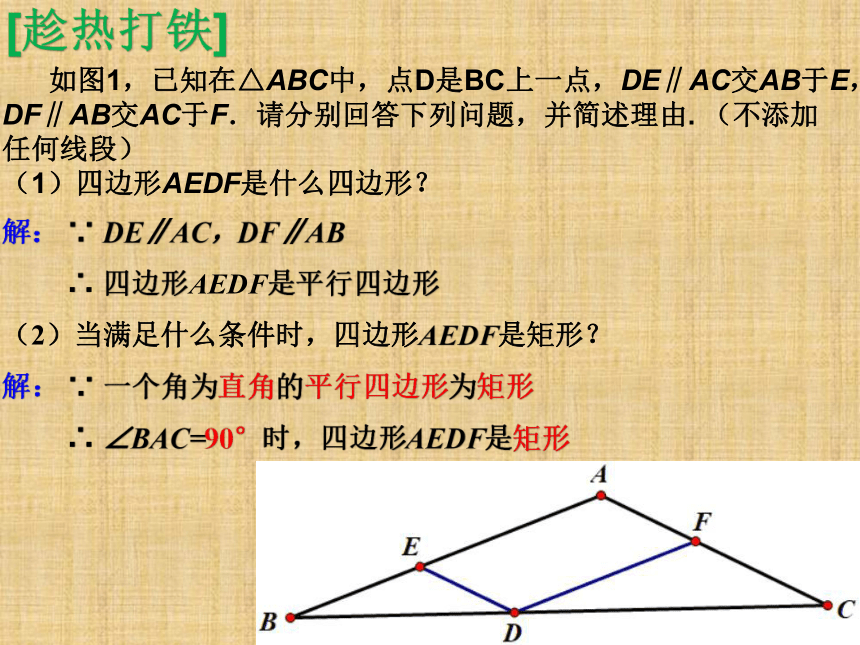
如图1,已知在△ABC中,点D是BC上一点,DE∥AC交AB于E,DF∥AB交AC于F.请分别回答下列问题,并简述理由. (不添加任何线段)
(1)四边形AEDF是什么四边形?
解: ∵ DE∥AC,DF∥AB
∴ 四边形AEDF是平行四边形
(2)当满足什么条件时,四边形AEDF是矩形?
解: ∵ 一个角为直角的平行四边形为矩形
∴ ∠BAC=90°时,四边形AEDF是矩形
[趁热打铁]
(3)当满足什么条件时,四边形AEDF是菱形?
解:∵ 有一组邻边相等的平行四边形是菱形
∴ 当AD平分∠BAC时,四边形AEDF是菱形
[趁热打铁]
(4)当满足什么条件时,四边形AEDF是正方形?
解:∵既是矩形又是菱形的四边形是正方形,
∴∠BAC=90°且AD平分∠BAC时,四边形AEDF是正方形.
[趁热打铁]
【变式训练】
已知: 如图, 在△ABC中, ∠BAC=90°, AD平分∠BAC, DE⊥AB, DF⊥AC, 垂足分别是E,F.
求证:四边形AEDF是正方形.
A
E
D
F
B
C
证明:∵∠BAC=90°, DE⊥AB, DF⊥AC,
∴四边形AEDF是矩形.
又∵ AD平分∠BAC, DE⊥AB, DF⊥AC,
∴DE=DF.
∴四边形AEDF是正方形.
【梳理反思】
1、学了什么?
2、悟到什么?
3、质疑发现?
【提示】 1.学了什么是梳理,建构知识系统;
2.悟到什么是反思,落实过程方法;
3.质疑发现是挖潜,孕育批判研究。
判定正方形的两条主要途径:
正方形
+
先判定矩形
菱形条件
(1)
一组邻边相等
或对角线互相垂直
正方形
+
先判定菱形
矩形条件
(2)
一个直角
或对角线相等
通过本节课的学习,你觉得正方形主要有哪些判定途径呢?
【佳作欣赏】
1. 必做题:
课本25页习题1.8第1、2、3题.
2. 选做题:
课本25页习题1.8第4题.
3.放飞题:
画一张思维导图,呈现本章节知识点
【学习延续】
谢谢各位!
1.3.2 正方形的判定
1.在平行四边形的基础上对矩形、菱形的判定
[温故而知新]
有一个角是直角
或对角线相等
平行四边形
矩形
菱形
有一组邻边相等
或对角线互相垂直
一个角是直角
有一个角是直角且一组邻边相等的平行四边形叫做正方形
正方形的两条对角线互相垂直平分且相等,
每条对角线平分一组对角
正方形的对边平行且相等
正方形的四个角都是直角
边
对角线
角
2.正方形的定义及性质
正方形的性质
且一组邻边相等
[温故而知新]
平行四边形
正方形
做一做:将矩形纸片对折两次,怎样裁剪才能使剪下的三角形
展开后是个正方形?
(1)
(2)
(3)
(4)
剪口与折痕成 45°角
菱形
问题2:满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
或对角线互相垂直
问题3:满足怎样条件的菱形是正方形?
一个角是直角
或对角线相等
正方形
1.有一组邻边相等的矩形是正方形.
2.对角线互相垂直的矩形是正方形.
3.有一个角是直角的菱形是正方形.
4.对角线相等的菱形是正方形.
定理
[实践出真知]
[小试牛刀]
1. 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
D
2.下列说法不正确的是( )
A.对角线互相垂直的矩形是正方形
B.对角线相等的菱形是正方形
C.对角线互相垂直且相等的四边形是正方形
D.有一个角是直角的菱形是正方形
C
证明:∵BF∥CE,CF∥BE
∴四边形BECF是平行四边形
又∵在矩形ABCD中,BE平分∠ABC,
CE平分∠DCB
∴∠EBA=∠ECB=45°
∴BE=CE
∴四边形BECF是菱形
又∵∠BEC=90°
∴四边形BECF是正方形.
如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
[范例精讲]
如图1,已知在△ABC中,点D是BC上一点,DE∥AC交AB于E,DF∥AB交AC于F.请分别回答下列问题,并简述理由. (不添加任何线段)
(1)四边形AEDF是什么四边形?
解: ∵ DE∥AC,DF∥AB
∴ 四边形AEDF是平行四边形
(2)当满足什么条件时,四边形AEDF是矩形?
解: ∵ 一个角为直角的平行四边形为矩形
∴ ∠BAC=90°时,四边形AEDF是矩形
[趁热打铁]
(3)当满足什么条件时,四边形AEDF是菱形?
解:∵ 有一组邻边相等的平行四边形是菱形
∴ 当AD平分∠BAC时,四边形AEDF是菱形
[趁热打铁]
(4)当满足什么条件时,四边形AEDF是正方形?
解:∵既是矩形又是菱形的四边形是正方形,
∴∠BAC=90°且AD平分∠BAC时,四边形AEDF是正方形.
[趁热打铁]
【变式训练】
已知: 如图, 在△ABC中, ∠BAC=90°, AD平分∠BAC, DE⊥AB, DF⊥AC, 垂足分别是E,F.
求证:四边形AEDF是正方形.
A
E
D
F
B
C
证明:∵∠BAC=90°, DE⊥AB, DF⊥AC,
∴四边形AEDF是矩形.
又∵ AD平分∠BAC, DE⊥AB, DF⊥AC,
∴DE=DF.
∴四边形AEDF是正方形.
【梳理反思】
1、学了什么?
2、悟到什么?
3、质疑发现?
【提示】 1.学了什么是梳理,建构知识系统;
2.悟到什么是反思,落实过程方法;
3.质疑发现是挖潜,孕育批判研究。
判定正方形的两条主要途径:
正方形
+
先判定矩形
菱形条件
(1)
一组邻边相等
或对角线互相垂直
正方形
+
先判定菱形
矩形条件
(2)
一个直角
或对角线相等
通过本节课的学习,你觉得正方形主要有哪些判定途径呢?
【佳作欣赏】
1. 必做题:
课本25页习题1.8第1、2、3题.
2. 选做题:
课本25页习题1.8第4题.
3.放飞题:
画一张思维导图,呈现本章节知识点
【学习延续】
谢谢各位!
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
