北师大版九年级上册数学 2.1.2一元二次方程的解的估算 课件(共20张PPT)
文档属性
| 名称 | 北师大版九年级上册数学 2.1.2一元二次方程的解的估算 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 807.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
解一元二次方程(二)
1、解一元二次方程的基本思路
2、什么样的方程可用直接开平方法解
原方程变为(x+m)2=n(n ≥0)或者
x2=p(p≧0)的形式(其中m、n、p是常数).
当n<0(p<0)时,原方程无解。
二次方程
一次方程
降次
转化
3、解一元二次方程
1) 2(X - 8)2 = 50
2) (X - 2)2 - 36 = 0
3) (2X+3)2 + 1 = 0
因式分解的完全平方公式
二次项系数为1的完全平方式:
常数项等于一次项系数一半的平方
配成完全平方式
1
4
你发现了什么规律?
移项
两边加上12的一半62,使左边配成完全平方式
左边写成完全平方的形式
开平方
变成了(x+m)2=n的形式
X1,X2都是原方程的根吗?
把二次方程转化成两个一次方程
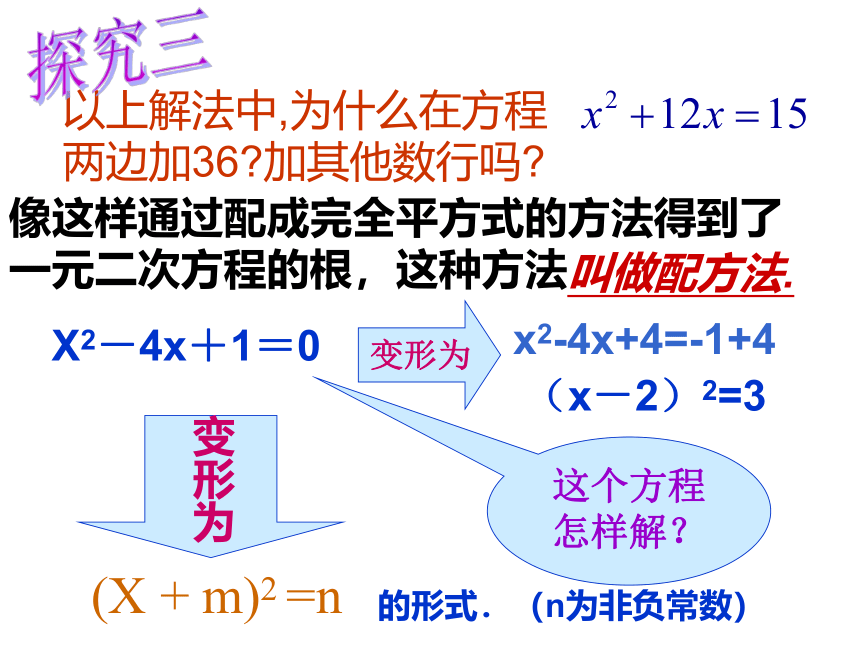
以上解法中,为什么在方程 两边加36 加其他数行吗
像这样通过配成完全平方式的方法得到了一元二次方程的根,这种方法
叫做配方法.
这个方程怎样解?
变形为
的形式.(n为非负常数)
变形为
X2-4x+1=0
(x-2)2=3
x2-4x+4=-1+4
(X + m)2 =n
我们刚才解的两个方程
X2-4x+1=0
你觉得用配方法解一元二次方程的一般步骤有哪些?
最关键的是哪一步?
移项
两边加上12的一半62,使左边配成完全平方式
左边写成完全平方的形式
开平方
变成了(x+m)2=n的形式
把二次方程转化成两个一次方程
用配方法解二次项系数为1的一元二次方程的步骤:
移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
配方的关键是, 方程两边同时加上一次项系数一半的平方
1、把一元二次方程通过配成完全平方式的方法得到了方程的根,这种解一元二次方程的方法叫做配方法.
注意:配方时, 方程两边同时加上的是一次项
项系数一半的平方.
2、用配方法解一元二次方程的一般步骤
(1)移项:把常数项移到方程的右边;
(2)配方:方程两边都加上一次项系数一半的平方;
(3)开方:根据平方根意义,方程两边开平方;
(4)求解:解一元一次方程;
1.用配方法解方程 X2 + 8X + 7 = 0方程可化为( )
A(x-4)2=9 B(x+4)2=9
C(x-8)2=16 C(x+8)2=57
2.用配方法解方程 x2 + x = 2 应把方程两边同时加上( )
B
A
B
C
D
A
3.若代数式X2 + 2(m+1)X + 25是完全平方式,则m的值是( )
A、4 B、 - 6 C、4或 – 6 D、 - 1
C
拓展延伸
试试你的应用能力
若 X2+Y2+4X-6Y+13=0,求Xy的值。
结束寄语
配方法是一种重要的数学方法,即配方法可以助你到达希望的顶点.
一元二次方程也是刻画现实世界的有效数学模型.
这节课最关键的是用了转化的数学方法,再次体会数学中的由未知转化为已知。
下课了!
列方程解应用题:
学校要组织一次篮球比赛,每两个队之间只进行一次比赛,如果一共要安排18场比赛,组织者需要安排多少个队参加比赛?
提示:单循环比赛的总场数=
解:设要组织X个队参加比赛
根据题意得:
3、填空:配成完全平方式
(1) X2-2X+( )=(X-1)2
(2) X2+6X+( )=(X+3)2
(3) X2-4X+4=(X - )2
(4) X2+( )+ 36 =(X+6 )2
1
9
2
12X
練習作業二:
在括號內填入適當的值:
1) X2 +4X+( ) =(X+ )2
2) X2-10X+( ) =(X - )2
3) X2 +X+( ) =(X+ )2
4) X2-3X+( ) =(X - )2
5) Y2 -12Y+( ) =(Y - )2
思考:先用配方法解下列方程:
(1) x2-2x-1=0 (2) x2-2x+4=0
(3) x2-2x+1=0
然后回答下列问题:
(1)你在求解过程中遇到什么问题?你是怎样处理所遇到的问题的?
(2)对于形如x2+px+q=0这样的方程,在什么条件下才有实数根?
3、解一元二次方程
1) 2(X - 8)2 = 50
2) (2 X - 1)2 + 36 = 0
3) X2 + 6X + 9 = 25
4) X2 – 4X + 4 = 3
解一元二次方程(二)
1、解一元二次方程的基本思路
2、什么样的方程可用直接开平方法解
原方程变为(x+m)2=n(n ≥0)或者
x2=p(p≧0)的形式(其中m、n、p是常数).
当n<0(p<0)时,原方程无解。
二次方程
一次方程
降次
转化
3、解一元二次方程
1) 2(X - 8)2 = 50
2) (X - 2)2 - 36 = 0
3) (2X+3)2 + 1 = 0
因式分解的完全平方公式
二次项系数为1的完全平方式:
常数项等于一次项系数一半的平方
配成完全平方式
1
4
你发现了什么规律?
移项
两边加上12的一半62,使左边配成完全平方式
左边写成完全平方的形式
开平方
变成了(x+m)2=n的形式
X1,X2都是原方程的根吗?
把二次方程转化成两个一次方程
以上解法中,为什么在方程 两边加36 加其他数行吗
像这样通过配成完全平方式的方法得到了一元二次方程的根,这种方法
叫做配方法.
这个方程怎样解?
变形为
的形式.(n为非负常数)
变形为
X2-4x+1=0
(x-2)2=3
x2-4x+4=-1+4
(X + m)2 =n
我们刚才解的两个方程
X2-4x+1=0
你觉得用配方法解一元二次方程的一般步骤有哪些?
最关键的是哪一步?
移项
两边加上12的一半62,使左边配成完全平方式
左边写成完全平方的形式
开平方
变成了(x+m)2=n的形式
把二次方程转化成两个一次方程
用配方法解二次项系数为1的一元二次方程的步骤:
移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
配方的关键是, 方程两边同时加上一次项系数一半的平方
1、把一元二次方程通过配成完全平方式的方法得到了方程的根,这种解一元二次方程的方法叫做配方法.
注意:配方时, 方程两边同时加上的是一次项
项系数一半的平方.
2、用配方法解一元二次方程的一般步骤
(1)移项:把常数项移到方程的右边;
(2)配方:方程两边都加上一次项系数一半的平方;
(3)开方:根据平方根意义,方程两边开平方;
(4)求解:解一元一次方程;
1.用配方法解方程 X2 + 8X + 7 = 0方程可化为( )
A(x-4)2=9 B(x+4)2=9
C(x-8)2=16 C(x+8)2=57
2.用配方法解方程 x2 + x = 2 应把方程两边同时加上( )
B
A
B
C
D
A
3.若代数式X2 + 2(m+1)X + 25是完全平方式,则m的值是( )
A、4 B、 - 6 C、4或 – 6 D、 - 1
C
拓展延伸
试试你的应用能力
若 X2+Y2+4X-6Y+13=0,求Xy的值。
结束寄语
配方法是一种重要的数学方法,即配方法可以助你到达希望的顶点.
一元二次方程也是刻画现实世界的有效数学模型.
这节课最关键的是用了转化的数学方法,再次体会数学中的由未知转化为已知。
下课了!
列方程解应用题:
学校要组织一次篮球比赛,每两个队之间只进行一次比赛,如果一共要安排18场比赛,组织者需要安排多少个队参加比赛?
提示:单循环比赛的总场数=
解:设要组织X个队参加比赛
根据题意得:
3、填空:配成完全平方式
(1) X2-2X+( )=(X-1)2
(2) X2+6X+( )=(X+3)2
(3) X2-4X+4=(X - )2
(4) X2+( )+ 36 =(X+6 )2
1
9
2
12X
練習作業二:
在括號內填入適當的值:
1) X2 +4X+( ) =(X+ )2
2) X2-10X+( ) =(X - )2
3) X2 +X+( ) =(X+ )2
4) X2-3X+( ) =(X - )2
5) Y2 -12Y+( ) =(Y - )2
思考:先用配方法解下列方程:
(1) x2-2x-1=0 (2) x2-2x+4=0
(3) x2-2x+1=0
然后回答下列问题:
(1)你在求解过程中遇到什么问题?你是怎样处理所遇到的问题的?
(2)对于形如x2+px+q=0这样的方程,在什么条件下才有实数根?
3、解一元二次方程
1) 2(X - 8)2 = 50
2) (2 X - 1)2 + 36 = 0
3) X2 + 6X + 9 = 25
4) X2 – 4X + 4 = 3
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
